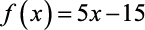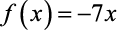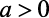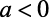Revise agora Função Polinomial do 1º grau. Sempre cai nas provas. Aprenda as Classificações, os Gráficos, como resolver as questões, e como extrair a Raiz da Função. Dá sim para aprender e gabaritar nos temas clássicos da Matemática. Aqui você aprende.
Aprenda a resolver questões de Função Polinomial do 1º Grau. É básico. Todo ano cai nas provas doEnem, do Encceja, e nos vestibulares. Confira agora o passo a passo no Resumo de Matemática Básica. Têm o conceito, os temas fundamentais, exemplos, exercícios resolvidos, e um simulado pra você responder depois e testar o seu nível.
Os enunciados de Polinômios são conhecidos de todos. É bem simples para identificar. Veja o que é uma Função Polinomial do 1º Grau.
Dados dois conjuntos A e B não vazio, temos que função é a relação onde para cada x pertencente a um conjunto A corresponde a um, e somente um, y pertencente a um conjunto B. Entendeu, ou complicou?
A Função Polonomial do 1º Grau
Veja no resumo agora como é simples a Função Polinomial de 1º Grau. É uma aula bem didática, simples e rápida. E você compreende e aprende.
As dicas do professor Lucas: O conceito de função é um dos mais importantes da matemática. Ele está sempre presente na relação entre duas grandezas variáveis. Assim são exemplos de funções:
- – O valor a ser pago numa corrida de táxi é função do espaço percorrido;
- – A área de um quadrado é função da medida do seu lado;
- – Em um termômetro, a temperatura é dada em função do comprimento da coluna de mercúrio.
Viu como não tem mistério? Muito boa esta aula do professor Lucas Borguesan, do canal do Curso Enem Gratuito.
Como escrever uma função
Temos que uma função polinomial do 1º grau, é toda função escrita na forma: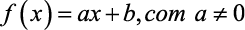
- Exemplos:
- a) – Função afim

- b) – Função linear)

Dica 1 – Pronto para gabaritar na prova de matemática do Enem? Faça uma revisão com esta aula sobre Equações Polinomiais do 1º grau – https://blogdoenem.com.br/equacoes-polinomiais-1o-grau-matematica-enem/
Raiz da Função Polinomial
Rais é o valor de x que zera a função. Podemos utilizar esta demonstração pra você entender: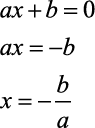
Ponto que intercepta o eixo y
Temos como valor que intercepta o eixo y (eixo das ordenadas) o coeficiente b. Pois: 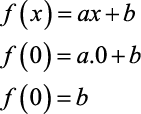
Dica 2 – Já sabe tudo sobre Conhecimentos Geométricos? Revise com esta aula sobre Escalas e fique pronto para a prova de Matemática do Enem – https://blogdoenem.com.br/escalas-matematica-enem/
Gráfico da Função Polinomial do 1º Grau
O gráfico de uma função polinomial do 1º grau é uma reta, com isso precisamos encontrar dois pontos, pois por dois pontos distintos passa uma única reta.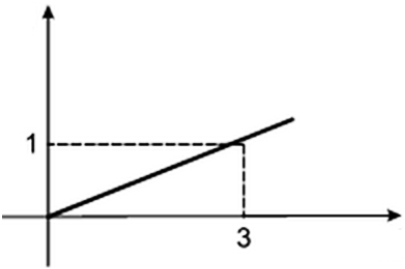 No gráfico acima temos uma função linear, escrita na forma:
No gráfico acima temos uma função linear, escrita na forma: 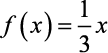
Veja como resolver as Equações de 1º grau
Confira agora com o professor Sérgio Sarkis um jeito simples e rápido para você resolver problemas com Polinômios de Primeiro Grau:
Excelente o resumo. Vamos continuar, que agora tem classificação de polinômios.
Classificação da Função Polinomial
Numa função polinomial do 1º grau
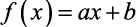 as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra:
as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra:
- Função Crescente

- Função decrescente

Dica 3 – Entenda como converter as unidades de medida de Comprimento e Área em mais esta aula de Matemática Enem – https://blogdoenem.com.br/volume-capacidade-matematica-enem/
Exercício Resolvido
(Enem 2ª aplicação 2010) As sacolas plásticas sujam florestas, rios e oceanos e quase sempre acabam matando por asfixia peixes, baleias e outros animais aquáticos. No Brasil, em 2007, foram consumidas 18 bilhões de sacolas plásticas. Os supermercados brasileiros se preparam para acabar com as sacolas plásticas até 2016. Observe o gráfico a seguir, em que se considera a origem como o ano de 2007.
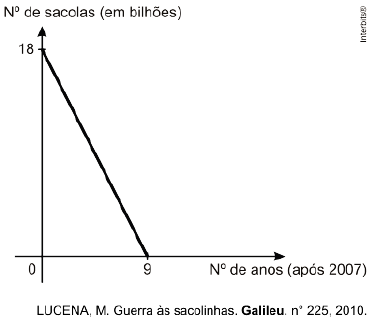
De acordo com as informações, quantos bilhões de sacolas plásticas serão consumidos em 2011?
- a) 4,0
- b) 6,5
- c) 7,0
- d) 8,0
- e) 10,0
Gabarito: [E]
Seja a função N de R em R, definida por N(n)=na+b em que N(n) é o número de sacolas consumidas, em bilhões, n anos após 2007.
Do gráfico, temos que o valor inicial de 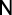 é
é 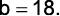
A taxa de variação da função 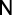 é dada por
é dada por
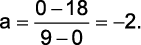
Desse modo, segue que 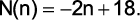
Queremos calcular o número de sacolas consumidas em 2011, ou seja, 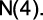
Portanto , 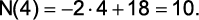
A Função de 2º grau
Saiba mais sobre Função Polinomial do 2º grau nesta aula do canal do Curso Enem Gratuito com o professor Sérgio Sarkis:
Mandou bem o professor Sarkis. Agora, é com você para resolver os exercícios.
Desafios – Exercícios sobre Função Polinomial do 1º grau
Questão 1 – função polinomial do 1º grau
Uma estudante oferece serviços de tradução de textos em língua inglesa. O preço a ser pago pela tradução inclui uma parcela fixa de R$ 20,00 mais R$ 3,00 por página traduzida. Em determinado dia, ela traduziu um texto e recebeu R$ 80,00 pelo serviço. Calcule a quantidade de páginas que foi traduzida.
Questão 2 – função polinomial do 1º grau
Em certa cidade, acontece anualmente uma corrida, como parte dos eventos comemorativos pela sua emancipação política. Em 2000, o comitê organizador da corrida permitiu a participação de 1500 pessoas; e, em 2005, a participação de 1800 pessoas. Devido as condições de infraestrutura da cidade, o comitê decidiu limitar o número de participantes da corrida. Nesse sentido, estudos feitos concluíram que o número máximo n(t) de participantes, no ano t, seria dado pela função afim n(t)=at+b, onde a e b são constantes.
Com base nessas informações, conclui-se que, no ano de 2010, o número máximo de participantes na corrida será de:
- a) 1900
- b) 2100
- c) 2300
- d) 2500
- e) 2700
Questão 3
(Enem 2011) As frutas que antes se compravam por dúzias, hoje em dia, podem ser compradas por quilogramas, existindo também a variação dos preços de acordo com a época de produção. Considere que, independente da época ou variação de preço, certa fruta custa R$1,75 o quilograma. Dos gráficos a seguir, o que representa o preço m pago em reais pela compra de n quilogramas desse produto é
a) 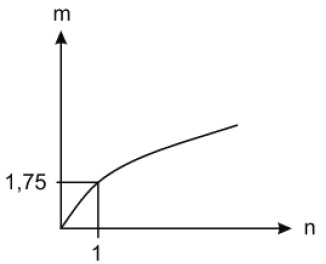
b) 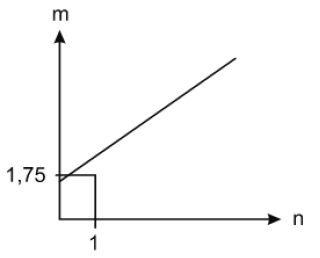
c) 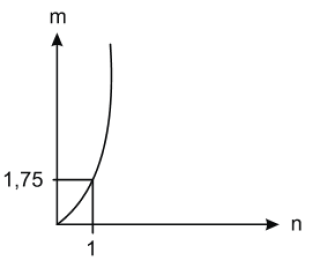
d) 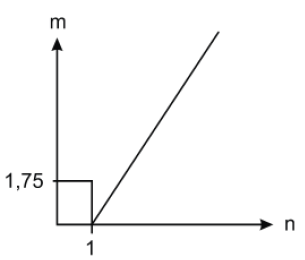
e) 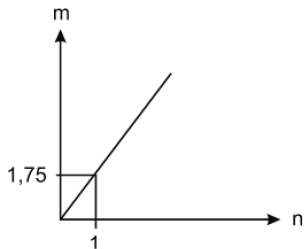
Questão 4
O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4300 vagas no setor, totalizando 880.605 trabalhadores com carteira assinada.
Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010
Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano. Considerando-se que y e x representem, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é
- a) y=4300x
- b) y=884905x
- c) y=872005+4300x
- d) y=876305+4300x
- e) y=880605+4300x
Questão 5 – função polinomial do 1º grau
Em fevereiro, o governo da Cidade do México, metrópole com uma das maiores frotas de automóveis do mundo, passou a oferecer à população bicicletas como opção de transporte. Por uma anuidade de 24 dólares, os usuários têm direito a 30 minutos de uso livre por dia. O ciclista pode retirar em uma estação e devolver em qualquer outra e, se quiser estender a pedalada, paga 3 dólares por hora extra.
Revista Exame, 21 de abr. 2010.
A expressão que relaciona o valor f pago pela utilização da bicicleta por um ano, quando se utilizam x horas extras nesse período é:
- a) f(x)=3x
- b) f(x)=24
- c) f(x)=27
- d) f(x)=3x+24
- e) f(x)=24x+3
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!