Confira aula gratuita e dicas importantes para você dominar as Funções Algébricas de 2° Grau. Perca o medo de resolver Equações. A hora é de afastar o fantasma da prova de matemática do Enem ou do vestibular. Vem!
A Função Polinomial do 2° Grau, também conhecida como Função Quadrática, é uma função real definida por: f(x) = ax2 + bx + c na qual a, b e c são coeficientes reais, sendo a ≠ 0. Revisão gratuita abaixo para o Enem e o Vestibular.
Vamos começar pelo básico do básico: A função polinomial de 2º Grau também é chamada de Função Quadrática. Veja a seguis exemplos de funções quadráticas:
a) y = x2 – 7x + 3, na qual a = 1, b = -7 e c = 3
b) y = – x2 + x + 9, na qual a = – 1, b = 1 e c = 9
As Funções Algébricas de 2° Grau
Definimos equações do segundo grau na incógnita x a toda equação que pode ser escrita na forma reduzida: ax² + bx + c = 0
Onde a, b e c são números reais e onde a é obrigatoriamente diferente de zero. Assim, a é o coeficiente de x², b é o coeficiente de x e c é o termo independente. Assim sendo:
2x² + 3x – 5 = 0; o coeficiente a é 2; o coeficiente b é 3 e o termo independente c é -5
A lei pela qual uma função é estabelecida é: f(x) = ax² + bx + c, com a, b e c números reais e a ≠ 0, é denominada função do 2º grau. De uma maneira geral, podemos determinar que:
F: R -> R tal que f(x) = ax² + bx + c, com a pertencente R*, b pertencente a R, C pertencente R.
Resumo sobre Funções
Veja com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, uma introdução sobre Funções:
.
Funções Algébricas de 2º Grau no dia a dia
Um comportamento bastante comum dos estudantes ao se depararem com fórmulas matemáticas é se perguntar: por que eu preciso saber disso? Ao contrário do que pensa a maioria, decifrar tantas fórmulas não serve apenas para ter uma boa nota na prova do Enem.
As funções de 2º grau, por exemplo, são bastante úteis em nosso cotidiano. Além de usá-las em disciplinas como física, esse conhecimento será aplicado no seu futuro profissional. Se o seu desejo é seguir a área das ciências biológicas, a função de 2º grau será aplicada para estudar a fotossíntese das plantas.
Se a sua intenção é ingressar na faculdade de contabilidade ou de administração, você vai se deparar novamente com essa função. Ela será um requisito básico para calcular a receita e o lucro de uma empresa, por exemplo.
Veja um exemplo de uma questão que poderia muito bem fazer parte de uma avaliação do curso de Administração:
Um fabricante vende, mensalmente, x unidades de um determinado artigo por R(x) = x² – x, sendo o custo da produção dado por C(x) = 2x² – 7x + 8. Quantas unidades devem ser vendidas mensalmente, de modo que se obtenha o lucro máximo?
Viu só? Para mesurar os lucros da empresa, o administrador precisa conhecer a função de 2º grau.
Melhor forma para aprender Funções
Você vai precisar entender algumas premissas básicas. Confira:
1. O grau de um termo independente é determinado pelo seu expoente, ou seja, as funções de segundo grau são dadas por um polinômio de segundo grau.
2. Conclui-se então que as funções de segundo grau têm como maior expoente o numeral 2.
3. O gráfico que representa essa função é uma curva que chamamos de parábola.
4. Uma função quadrática do segundo grau é expressa da seguinte maneira: F (x) = ax² + bx + c, onde a é diferente de zero.
É o termo ax² que determina a função de segundo grau. Esse, portanto, será o maior grau da função. Quando uma função possui um termo de ax³, será uma função polinominal de terceiro grau, não de segundo.
Existem ainda funções de segundo grau incompletas. Veja os exemplos:
f (x) = x²
f (x) = ax²
f (x) = ax²+ bx
f (x) = ax² + c
O termo de segundo grau pode aparecer isoladamente. Exemplo: y = ax² ou estar junto a um termo de primeiro grau: y = ax² + bx. Ou ainda vir unido a um termo independente como em y = ax2 + c.
Embora seja diferente das funções lineares, também são fáceis de serem trabalhadas. É importante que você lembre-se de que ela é representada por uma parábola.
É importante saber também que o ponto mais baixo da curva (aquele em que a curva se intercepta com o eixo Y) é o ponto de coordenadas (0,0). Este ponto é conhecido como vértice da parábola.
Aula Gratuita de Funções
Veja com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, uma revisão online completa para o Vestibular e o Exame Nacional do Ensino Médio
Função do 2º grau ou função quadrática
Para a entender a Função de 2º Grau – importante tema para o Enem e os vestibulares -, acompanhe o seguinte raciocínio: na física, sabe-se que a trajetória de um projétil lançado obliquamente em relação ao solo horizontal é um arco de parábola com a concavidade voltada para baixo.


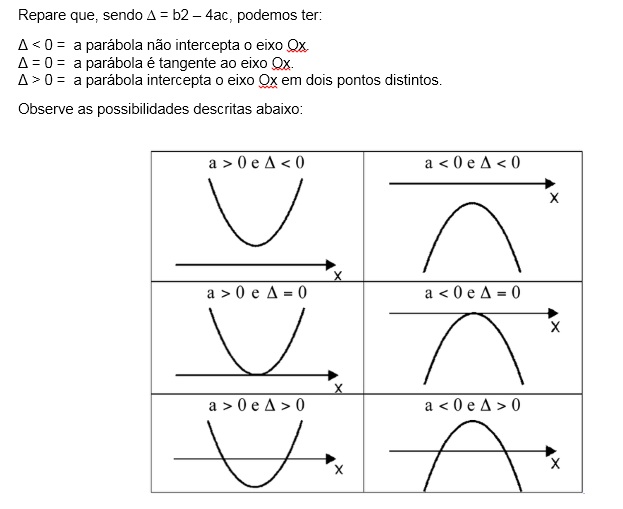
Assista a aula abaixo para complementar a introdução às funções do 2º grau:
Dicas de Matemática Enem:
Dica 1: o que mais cai na prova de Matemática do Enem? Veja aqui as dicas sobre Relações Matemáticas
Dica 2: Já sabe tudo sobre Regra de Três Composta? Veja o que cai aqui nesta Revisão de Regra de Três Composta
Dica 3: Você o que é e como calcular um produto cartesiano? Confira esta revisão de Plano e Produto Cartesiano
Este post foi elaborado por Milena Cristina Godoy. Milena é médica veterinária. Estudou matemática e estatística durante nove anos, período em que trabalhou com análise de dados durante o desenvolvimento de pesquisas na sua área de atuação. Twitter: @vetempregos



