Regra de Três Composta. Resumo de Matemática Enem e vestibular

Veja aqui revisão de Regra de Três Composta para o Enem e os vestibulares.  Fique aqui com a gente! Antes de mergulhar nos exercícios que vão ajudar você a dominar a Regra de Três Composta, uma pergunta essencial: Você lembra certinho como fazer a Regra de Três?

Se você não lembra, aqui tem uma aula completa com o básico de Regra de Três Simples. Revise aqui neste post do Blog do Enem e depois retorne para continuar com a Regra de Três Composta: https://blogdoenem.com.br/regra-de-tres-matematica/

  Confira agora no resumo gratuito com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito. Aprenda a Regra de Três Simples, e a Regra de Três Composta.

Você precisa ficar de olho aberto apra entender o que são as grandezas diretamente proporcionais, e as grandezas inversamente proporcionais. Na Regra de Três Simples você trabalha com “duas Grandezas”. E, na Regra de Três Composta, você trabalha com “Três ou mais grandezas”.  Veja agora, na prática, com o professor Sarkis.

  Conferiu como não é nada complicado? Você consegue sim aprender e mandar bem.

Regra de Três Composta

Agora, que você já está pronto para avançar para a Regra de Três Composta, considere a seguintes situações:

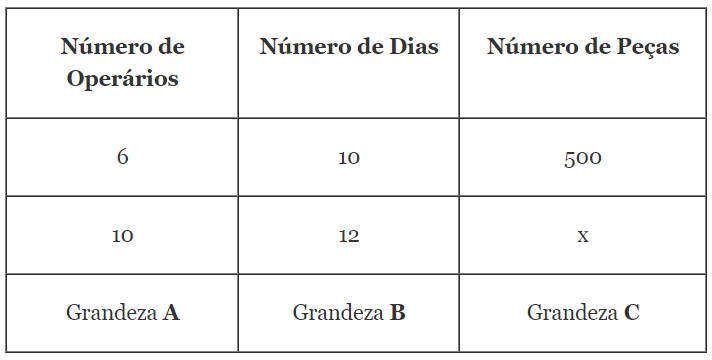
• Situação 1: Trabalhando durante 10 dias, 6 operários produzem 500 peças.
• Quantas peças desse mesmo tipo serão produzidas por 10 operários trabalhando 12 dias?

Observe no quadro abaixo como você pode ‘organizar’ a situação-problema para ajudar no racionínio de resolução. Perceba como associar as Grandezas para encontrar o caminho que leva à resposta.

As Grandezas na Regra de Três Composta

Releia o texto acima e denomine de Grandeza A o número de operários; de Grandeza B o número de dias; e, de Grandeza C o número de peças produzidas. Agora, no quadro a seguir, veja como ajuda a compor o raciocínio:

 Uma fábrica com 6 operários trabalhando durante 10 dias produziu 500 peças. Se você tiver na mesma fábrica, 10 operários trabalhando durante 12 dias, quantas peças serão produzidas. Este é “x” da questão, descobrir a quantidade de peças.) e

Relacionando somente as grandezas B e C, se aumentamos o número de dias, o número de peças fabricadas também aumenta, ou seja, as grandezas B e C são grandezas diretamente proporcionais.

Relacionando as grandezas A e C, se aumentamos o número de operários o número de peças fabricadas também aumenta, isto é, estas duas grandezas também são grandezas diretamente proporcionais. Logo, o valor da grandeza C será diretamente proporcional aos produtos dos valores das grandezas A e B.

Então, você estrutura da seguinte forma para buscar o resultado: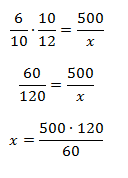

Resultado: x = 1000 peças

Saiba mais sobre a regra de três composta assistindo a vídeo aula totalmente gratuita e mande bem nas questões de matemática dos vestibulares e também do Enem.

Outro Exemplo de Regra de Três Composta

Situação 2: Um ciclista anda em média 400 km em 5 dias, se pedalar 6 horas por dia. Em quantos dias esse ciclista andará 600 km, se pedalar 9 horas por dia?

Da tabela abaixo temos:

Relacionando somente as grandezas B e C, quando aumentamos a grandeza B o número de dias diminuirá, isto é, as grandezas B e C são grandezas inversamente proporcionais.

Relacionando somente as grandezas A e C, quando aumentamos o número de quilômetros percorridos, o número de dias também aumentará, ou seja, as grandezas A e C são grandezas diretamente proporcionais.

Desta forma, a razão entre os valores da grandeza C será igual ao produto da razão entre os valores da grandeza A (diretamente proporcional) e da razão entre os valores da grandeza B (inversamente proporcional), ou seja, devemos escrever a razão inversa dos valores da grandeza B: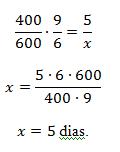

Dica 2 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas https://blogdoenem.com.br/category/cainaprova/matematica/

Aula Gratuita sobre Regra de Três Composta:

Exercício – Um folheto enviado pela Empresa Estadual de Águas informa que uma torneira, pingando 20 gotas por minuto, em 30 dias, desperdiça 100 litros de água. Na casa de Maria, uma torneira esteve pingando 30 gotas por minuto durante 50 dias. Calcule quantos litros de água foram desperdiçados na casa de Maria nestes 50 dias.

Resolução:

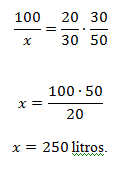
Reforço de Regra de Três

Veja agora com o professor Vinny uma aula bem focada, para ajudar você a fixar bem o conteúdo de Regra de Três.

O texto acima sobre Regra de Três Simples e sobre Regra de Três Composta foi preparado pelo professor Orlandino R. F. da Silva Junior para o Blog do Enem. Orlandino é formado em Matemática pela Universidade Federal de Santa Catarina e dá aulas de matemática em escolas da grande Florianópolis desde 2002. Skype: orfajr.