A maioria dos problemas de Matemática no Enem e nos vestibulares. envolve algum tipo de função. Elas estão até mesmo em geografia, biologia, química e física. Aprenda as características das funções lineares e funções quadráticas com este resumo!
Veja uma revisão focada de Matemática Enem para funções lineares e funções quadráticas. É dessa forma que são conhecidas as funções de 1º grau e as funções de 2º grau. É conteúdo certo no Enem e nos vestibulares.
Nos estudos da matemática, as funções descrevem a relação entre dois conjuntos de números através de uma lei de formação. Portanto, há uma relação entre os dois conjuntos de números, e um deles está ‘em função’ do outro.
O que são funções?
Considere a lei de formação abaixo:
y = x + 2
Esta é uma função linear, ou uma função de 1º grau. Observe que para cada valor de x substituído na equação pode-se calcular um valor para y. Se x=4, temos y = 4 + 2 = 6.
Além disso, podemos também calcular para saber qual valor de x teremos um certo valor de y. Por exemplo, para y = 5, qual seria o valor de x?
O procedimento é o seguinte:
- 5 = x + 2
- 5 – 2 = x
- 3 = x
- x = 3
Introdução rápida sobre Funções
Para ajudar você de maneira simples e descomplicada, o professor Lucas Borghesan, do canal do Curso Enem Gratuito, preparou um resumo sobre Como resolver questões de funções no Enem.
É bem prático. Veja agora, que vai ajudar você a perder o medo, e dominar o tema com a continuação desta aula depois do vídeo.
Viu só como dá, sim, pra você aprender funções e mandar bem no Enem?
Revise funções lineares: funções de 1º grau
A denominação de funções lineares ou de função de 1o grau é dada quando representamos a relação de y e x em um gráfico, podemos observar uma reta. O formato da função é:
y = ax + b
Sendo a o coeficiente angular da reta, ou seja, quanto maior o valor de a, maior vai ser a inclinação e para valores negativos, teremos retas decrescentes. O b é chamado de coeficiente linear, ou seja, é o local de cruzamento da reta no eixo y. Como exemplo, vamos utilizar a função dada anteriormente:
y = x + 2
Vemos que a = 1 e b = 2. Agora vamos criar uma tabela com alguns valores quaisquer x e calcular o valor de y e com eles construiremos um gráfico.
Vemos o seguinte: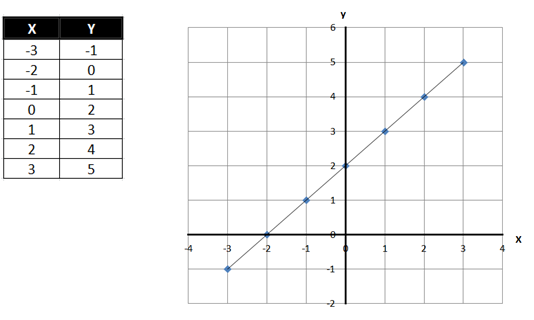
Videoaula sobre funções lineares ou de 1º grau
Veja aqui uma aula do Curso do Enem Gratuito sobre equação de primeiro grau, com o professor de Matemática Sérgio Sarkis:
Gostou do jeito do professor Sarkis, de resolver os problemas passo a passo com você: Muuito bom.
Funções quadráticas ou funções de 2º grau
As funções de 2o grau, também chamadas de funções quadráticas, caem bastante nos principais vestibulares e no Enem. Elas possuem o seguinte formato:
y = ax² + bx + c
O gráfico desta função tem o formato de uma parábola. Por isso, para valores positivos de a vemos uma parábola de concavidade para cima e para valores negativos de a vemos uma parábola de concavidade para baixo. Por exemplo:
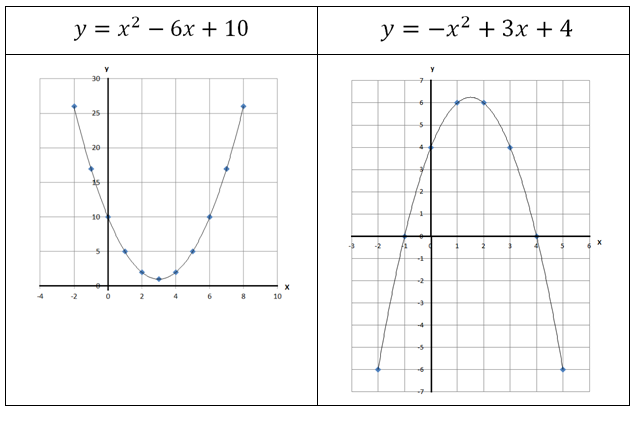
Os gráficos de funções de 2o grau possuem alguns pontos especiais. O primeiro é o vértice, que são os pontos de mínimo, caso a parábola seja de concavidade para cima, ou de máximo, caso a concavidade seja para baixo.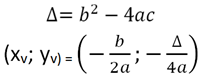
Por fim, os outros dois pontos importantes, caso existam, são os pontos de intersecção da linha com o eixo x, também chamados de raízes da função. Portanto, a condição de existência deles depende do valor do delta.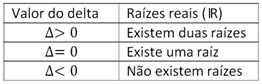
As raízes são encontradas utilizando a fórmula de Bhaskara: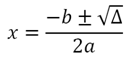
Vamos utilizar a função abaixo para encontrar as coordenadas do vértice e as raízes.
y = -x² + 3x + 4
Primeiramente vemos que a=-1, b=3 e c=4.
Então,
e as coordenadas do vértice são: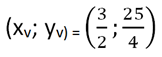
Os valores das raízes são: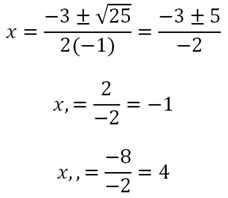
Dessa forma, podemos verificar a posição destes pontos no gráfico acima.
Resumo sobre a Fórmula de Bhaskara
Veja agora como resolver as equações de segundo grau usando a boa e velha conhecida, a Fórmula de Bhaskara. Confira com o professor Sérgio Sarkis.
Agora que você já viu o resumo sobre funções, aprendeu as funções lineares de Primeiro Grau, e aprendeu também as funções de Segundo Grau, chegou a hora de colocar os seus conhecimentos pra fora.
Exercícios sobre funções lineares
1. As projeções para a produção de arroz no período de 2012 – 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. Dessa forma, o quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.
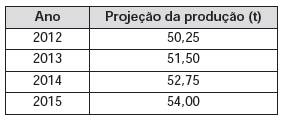
Portanto, a quantidade total de arroz, em toneladas, que deverá ser produzida no período de 2012 a 2021 será de A) 497,25. B) 500,85. C) 502,87. D) 558,75. E) 563,25. 2. A parte interior de uma taça foi gerada pela rotação de uma parábola em torno de um eixo z, conforme mostra a figura.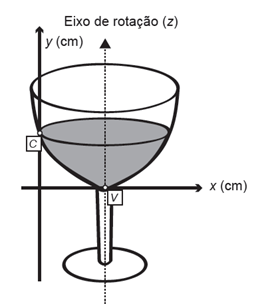 
A função real que expressa a parábola, no plano cartesiano da figura, é dada pela lei
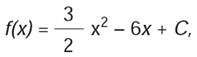
onde C é a medida da altura do líquido contido na taça, em centímetros. Sabe-se que o ponto V, na figura, representa o vértice da parábola, localizado sobre o eixo x. Nessas condições, a altura do líquido contido na taça, em centímetros, é
A) 1
B) 2
C) 4
D) 5
E) 6
Gabarito D
2. (ENEM – 2015) Um meio de transporte coletivo que vem ganhando espaço no Brasil é a van, pois realiza, com relativo conforto e preço acessível, quase todos os tipos de transportes: escolar e urbano, intermunicipal e excursões em geral. O dono de uma van, cuja capacidade máxima é de 15 passageiros, cobra para uma excursão até a capital de seu estado R$ 60,00 de cada passageiro. No entanto, se não atingir a capacidade máxima da van, cada passageiro pagará mais R$ 2,00 por lugar vago. Sendo x o número de lugares vagos, a expressão que representa o valor arrecadado V(x), em reais, pelo dono da van, para uma viagem até a capital é:
a) V(x) = 902x
b) V(x) = 930x
c) V(x) = 900 + 30x
d) V(x) = 60x + 2x²
e) V(x) = 900 – 30x – 2x²
Gabarito: E
3. (ENEM – 2015) O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00. Dessa forma, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. No entanto, a expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1 800 . (1,03)t. De acordo com a proposta do sindicato, o salário de um profissional de empresa com 2 anos de tempo de serviço será, em reais,
a) 7 416,00.
b) 3 819,24.
c) 3 709,62.
d) 3 708,00.
e) 1 909,62.
Gabarito: E
