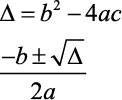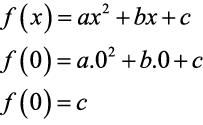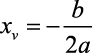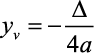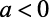Tire todas as suas dúvidas sobre Funções Polinomiais de 2o grau em mais esta aula de revisão para a prova de Matemática Enem que preparamos para você. Cai todo ano no Enem e no Vestibular. Confira abaixo.
Hora de Aprender Funções de uma vez por todas. Chega de perder pontosno Enem, nos vestibulares, ou nas provas do Encceja. confira com os professores Lucas Borguesan, e Sérgio Sarkis, ambos do canal do Curso Enem Gratuito, as dicas básicas sobre as Funções Polinomiais do 2º Grau.
A função é bem explorada nos vestibulares e no Enem. Ela é apresentada de diversas formas e inserida em diversos assuntos como Estatística, Matemática Financeira, e em várias situações problemas em outras áreas de conhecimento como Física, Biologia e Geografia.
Como aprender Funções Polinomiais
Nesta aula, o professor Lucas te ensina os conceitos de Funções Polinomiais e ainda te dá dicas de como resolver sem dificuldade os problemas matemáticos com funções.
As dicas básicas do professor Lucas
- Todo ano cai direto nas provas;
- Os alunos demonstram medo ou pavor com a palavra “função”, mas chegou a hora de resolver esse mistério.
- Veja no quadro os exemplos do professor para diferenciar Função, de Equação, e de Expressões Numéricas.
- Confira os exemplos das funções características com f(x)
– Revisão para você mandar bem no Enem e no Vestibular
Para você não esquecer, temos que as funções polinomiais do 2º grau são todas aquelas funções escritas da seguinte forma:
Veja estes Exemplos de Função Polinomial do 2º Grau:
a)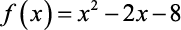 
b)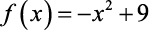 
Veja as Funções Matemáticas Básicas
Aprenda agora com o professor Sérgio Sarkis como resolver as questões mais básicas de Funções. E, a boa surpresa, é que mais de 60% das questões das provas de Matemática do Enem são de temas básicos, simples de se resolver.
Veja estes exemplos das provas do Encceja, de Ensino Médio, e que valem para o Enem tambéis. É pra você perder o medo e gabaritar nas próximas provas.
As dicas do professor Sarkis:
- As funções matemáticas são um assunto recorrente nos principais exames do país !
- Aproveita e vem pra nossa aula que o professor Sarkis te ajuda resolvendo um exercício sobre o conteúdo 😀
Veja o que é Raiz da Função:
- É o valor de x que zera a função.
- Vamos utilizar as mesmas fórmulas que você já conhece:
Entenda o Ponto que intercepta o eixo y:
- Temos como valor que intercepta o eixo y (eixo das ordenadas) o coeficiente c.
- Pois:
Portanto, o ponto que intercepta o eixo das ordenadas é o ponto (0;c)
O Vértice
- É o ponto em que se encontra o valor máximo ou mínimo de uma função polinomial do 2º grau. E podemos encontrar utilizando as seguintes fórmulas:
Entenda o Gráfico das Funções de 2º Grau:
O gráfico de uma função polinomial do 2º grau será uma parábola, como você pode observar no exemplo abaixo: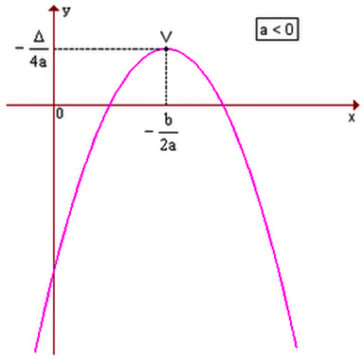
Analisando os gráficos, podemos chegar a algumas conclusões gerais:
- Parábola concavidade para baixo:
- Parábola concavidade para cima:
- Valor mínimo para uma função:
Para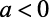 
, não teremos valor mínimo, pois a função tende a menos infinito.
Para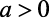 
, o valor mínimo será o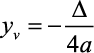 
Valor máximo para uma função: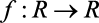 
Para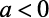 
, o valor máximo será o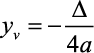 
Para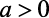 
, teremos valor mínimo, pois a função tende a menos infinito.
Dica 1 – O dia das provas está chegando, que tal revisar algumas aulas importantes. Revise tudo sobre Função Polinomial do 1º grau nesta aula de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-do-1o-grau-matematica-enem/
Veja um Exercício Resolvido
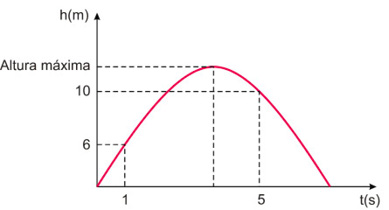
Um jogador de futebol, ao bater uma falta com barreira, chuta a bola de forma a encobri-la. A trajetória percorrida pela bola descreve uma parábola para chegar ao gol.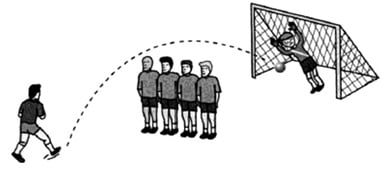
Sabendo-se que a bola estava parada no local da falta no momento do chute, isto é, com tempo e altura iguais a zero; sabendo-se, ainda, que, no primeiro segundo após o chute, a bola atingiu uma altura de 6 metros e, cinco segundos após o chute, ela atingiu altura de 10 metros; pode-se afirmar que, após o chute, a bola atingiu a altura máxima no tempo igual a:
- a) 3 segundos
- b) 3,5 segundos
- c) 4 segundos
- d) 4,5 segundos
- e) 5 segundos
Vamos resolver juntos, para você aprender de vez! 
De acordo com o gráfico, temos:
h(t) = a.t2 +b.t
Sabendo que h(1) = 6m e h(5) = 10m, temos o sistema:
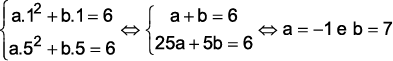
Portanto, h(t) = -t2 + 7t, logo a altura máxima será atingida para
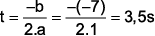
Está achando difícil? Revise então Polinômios de 1º Grau.
Veja aqui aula de introdução aos Polinômios para você revisar desde o mais básico para ir avançando depois. Bora lá. CLique na imagem para revisão online das Funções de 1º Grau. Assim você ‘faz um esquenta do cérebro’ e depois retorna para os Polinômios de 2º Grau:
Aula Gratuita
Exercício Resolvido. Mais um para você:
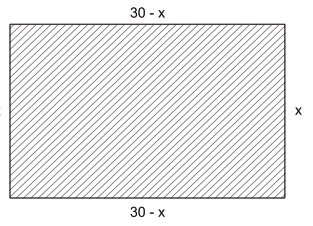
2. (Ufpb 2010) Em seus trabalhos de campo, os botânicos necessitam demarcar áreas de mata onde farão observações. Essas áreas são denominadas parcelas e, geralmente, usa-se corda para demarcá-las.
Nesse contexto, se uma parcela retangular for demarcada com 60m de corda, sua área será, no máximo, de:
a) 100m2
b) 175m2
c) 200m2
d) 225m2
e) 300m2
Resposta da questão 2: [D]
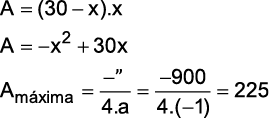
Desafios para você resolver e compartilhar
Questão1
(G1 – cftmg 2010) O conjunto imagem da função
f(x) = – 4 – 3x + x2, definida para todo x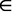 
R, está contido em
a)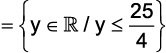 
b)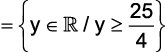 
c)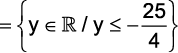 
d)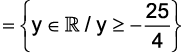 
Dica 2 – Acompanhe esta revisão sobre Equações Polinomiais do 1º e 2º grau e fique preparado para a prova de Matemática Enem – https://blogdoenem.com.br/equacoes-polinomiais-1o-e-2o-grau-matematica-enem/
Questão 2
(G1 – cftmg 2008) Uma casa retangular com 15 metros de comprimento e 10 metros de largura possui um jardim ao seu redor, como mostra a figura a seguir.
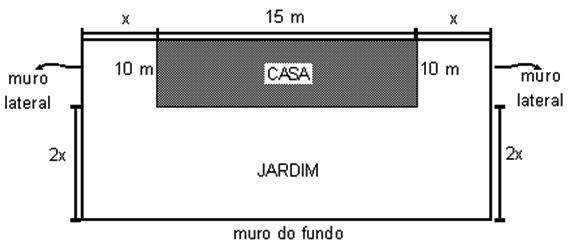
A expressão do valor da área A do jardim, em função de x, é
a) A(x) = 4×2 + 50x
b) A(x) = 5×2 + 25x
c) A(x) = 10×2 + 4x
d) A(x) = 15×2 + 10x
Questão 3
(Ufsm 2008) Durante um passeio noturno de barco, diversão preferida de um grupo de jovens, surgiu uma situação de perigo, em que houve necessidade de disparar um sinalizador para avisar o restante do grupo que ficara no acampamento.
A função que descreve o movimento do sinal luminoso é dada por h(t) = 30t – 3t2, onde h é a altura do sinal em metros e t, o tempo decorrido em segundos, desde o disparo até o momento em que o sinalizador cai na água. Assim, a altura máxima atingida pelo sinalizador e o tempo decorrido até cair na água são, respectivamente,
a) 75 m e 10 s
b) 75 m e 5 s
c) 74 m e 10 s
d) 74 m e 5 s
e) 70 m e 5 s
Questão 4
(G1 – cftmg 2007) O gráfico da função f : IR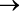 
IR, tal que f (x) = x2 – 10 x + 9 é uma parábola
a) cujo máximo é 5.
b) cujo mínimo é -16.
c) que intercepta o eixo das ordenadas no ponto (0,10).
d) que intercepta o eixo das abscissas nos pontos (-1,0) e (- 9,0).
Dica 3 – Revise tudo sobre os Logaritmos em mais esta aula de Matemática Enem, com definições e exercícios resolvidos para você gabaritar no Exame Nacional do Ensino Médio – https://blogdoenem.com.br/logaritmos-matematica-enem-2/
Questão 5
(Ufpb 2007) A função L(x) = -100x2 + 1200x – 2700 representa o lucro de uma empresa, em milhões de reais, onde x é a quantidade de unidades vendidas. Nesse contexto, considere as seguintes afirmações:
I. Se vender apenas 2 unidades, a empresa terá lucro.
II. Se vender exatamente 6 unidades, a empresa terá lucro máximo.
III. Se vender 15 unidades, a empresa terá prejuízo.
Está(ão) correta(s) apenas:
a) I
b) II
c) III
d) I e II
e) II e III
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
