Fique preparado para gabaritar na prova de Matemática do Enem revisando o conteúdo com esta aula completa sobre intervalos em R. Confira abaixo.
Veja o essencial sobre Intervalos em R nesta revisão de Matemática Enem e Vestibular. Confira como resolver problemas em Segmentos de Retas e questões de Intervalos Abertos ou Intervalos Fechados. Sempre cai!
Nem toda solução de um problema matemático é um número. Muitas vezes essa solução é um conjunto numérico contido em  .
.  Veja as Definições: Considere duas números reais a e b, com a<b.
Veja as Definições: Considere duas números reais a e b, com a<b.
- I) Intervalo aberto de extremos a e b
- É o conjunto
 .
. - Além da representação
 também utilizamos
também utilizamos  .
.
- Geometricamente, veja a representação na linha abaixo com o intervalo entre os pontos ‘a’ e ‘b’, sendo as bolinha de ‘a’ e de ‘b’ vazias na marcação:

II) Intervalo fechado de extremos ae b:
- É o conjunto
 .
. - Geometricamente representamos assim o intervalo fechado de extremos a e b, com as bolinhas ‘a’ e ‘b’ cheias na marcação dos pontos

III) Intervalo fechado à esquerda e aberto à direita extremos a e b
- É o conjunto
 .
. - Geometricamente representamos desta maneira (perceba a bolinha cheia em ‘a’ e vazia em ‘b’.

Aula Gratuita – Veja exemplos com exercícios resolvidos
Confira no resumo simples e rápido com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, como resolver problemas de Retas e Segmentos de Retas.
Muito bom o resumo. Vamos em frente aqui com os Intervalos.
IV) Intervalo aberto à esquerda e fechado à direita extremos a e b
- É o conjunto
 .
. - Geometricamente representamos

V) Intervalos infinitos
a) 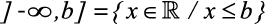

b) 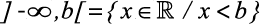

c) 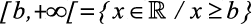

d) 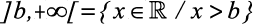

Exemplo com exercício resolvido:
Suponha que seu intervalo para almoço comece às 12hs e termine às 14:00hs . Usando a linguagem matemática teríamos 3 formas de representação:
1a) Almoço = 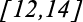
2a) Almoço = 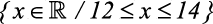
3a) Almoço : 
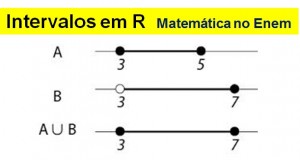
União e Intersecção de Intervalos
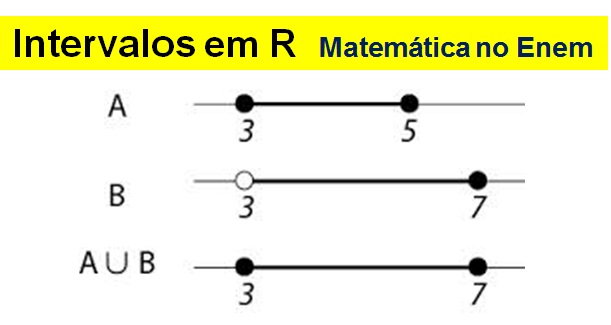
Considere como exemplo os intervalos A = [3,5] e B = ]3,7].
União de A e B

Intersecção de A e B

Desigualdades
Exemplo: Obtenha o conjunto solução das seguintes desigualdades abaixo.
1) 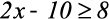
Resolução:
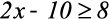
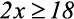
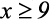
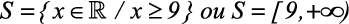
Veja Exercício resolvido:
2) 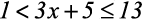
Resolução:
Chamamos essa desigualdade de inequação simultânea e resolvemos desse modo:

3) 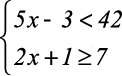
Resolução:
Como temos um sistema com duas inequações, obteremos o conjunto solução de cada uma delas.
A solução geral será um conjunto que satisfaz às duas simultaneamente, portanto, a intersecção das soluções individuais.
(I) 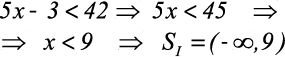
(II) 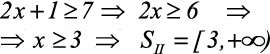
Solução Final: 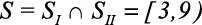
Desafios para você resolver e compartilhar
Questão 1
Em qual das alternativas abaixo está representada a intersecção entre os intervalos A = (1,9] e 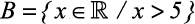 ?
?
a) 
b) 
c) 
d) 
e) 
Questão 2
(G1 – cps 2005) Dois jovens viveram concomitantemente durante um certo tempo na cidade de São Paulo. O primeiro jovem afirmou que mora na cidade a partir do ano indicado na inequação 2t – 3960 ≥ 0 e o segundo jovem morou na cidade antes do ano indicado na inequação 3t – 6000 ≤ 0, onde t é o ano do calendário.
Com estas informações pode-se dizer que os jovens viveram simultaneamente na cidade de São Paulo durante
a) 30 anos. b) 25 anos. c) 20 anos. d) 15 anos. e) 10 anos.
Dica 1 – Preparado para o Enem? Revise Matemática com esta aula sobre operações com números na forma decimal – https://blogdoenem.com.br/matematica-enem-operacoes-decimal/
Questão 3
(Pucmg 2004) Para se tornar rentável, uma granja deve enviar para o abate x frangos por dia, de modo que seja satisfeita a desigualdade 1,5x + 80 ≤ 2,5x – 20. Nessas condições, pode-se afirmar que o menor valor de x é:
a) 100 b) 200
c) 300 d) 400
Dica 2 – Matemática Enem – Aula sobre os critérios de divisibilidade em N – https://blogdoenem.com.br/matematica-enem-divisibilidade-n/
Questão 4
(Enem 2011) Uma indústria fabrica um único tipo de produto e sempre vende tudo o que produz. O custo total para fabricar uma quantidade q de produtos é dado por uma função, simbolizada por  , enquanto o faturamento que a empresa obtém com a venda da quantidade q também é uma função, simbolizada por
, enquanto o faturamento que a empresa obtém com a venda da quantidade q também é uma função, simbolizada por  . O lucro total
. O lucro total 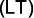 obtido pela venda da quantidade q de produtos é dado pela expressão
obtido pela venda da quantidade q de produtos é dado pela expressão 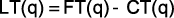 . Considerando-se as funções
. Considerando-se as funções 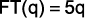 e
e 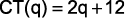 como faturamento e custo, qual a quantidade mínima de produtos que a indústria terá de fabricar para não ter prejuízo?
como faturamento e custo, qual a quantidade mínima de produtos que a indústria terá de fabricar para não ter prejuízo?
a) 0 b) 1 c) 3 d) 4 e) 5
Dica 3 – Matemática Enem – revise os Múltiplos e Divisores – https://blogdoenem.com.br/multiplos-e-divisores-enem/
Questão 5
(Enem 2005) O gás natural veicular (GNV) pode substituir a gasolina ou álcool nos veículos automotores. Nas grandes cidades, essa possibilidade tem sido explorada, principalmente, pelos táxis, que recuperam em um tempo relativamente curto o investimento feito com a conversão por meio da economia proporcionada pelo uso do gás natural. Atualmente, a conversão para gás natural do motor de um automóvel que utiliza a gasolina custa 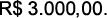 Um litro de gasolina permite percorrer cerca de
Um litro de gasolina permite percorrer cerca de 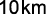 e custa
e custa 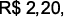 enquanto um metro cúbico de GNV permite percorrer cerca de
enquanto um metro cúbico de GNV permite percorrer cerca de 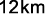 e custa
e custa 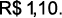 Desse modo, um taxista que percorra
Desse modo, um taxista que percorra 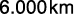 por mês recupera o investimento da conversão em aproximadamente:
por mês recupera o investimento da conversão em aproximadamente:
a) 2 meses. b) 4 meses. c) 6 meses. d) 8 meses. e) 10 meses.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
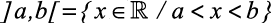 .
.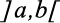 também utilizamos
também utilizamos 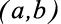 .
.
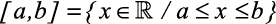 .
.
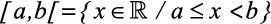 .
.
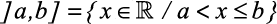 .
.



