Aprenda agora como resolver questões das quatro operações com números decimais: Adição; Subtração; Divisão; e Multiplicação. Veja também como transformar Frações em Números Decimais com os professores Lucas Borghesan, e Sérgio Sarkis. É pra gbaritar Matemática no Enem. Vem!
Você já se confundiu na hora de efetuar operações com números decimais? Fica em paz, porque é super normal. Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, as dicas básicas que vão fazer você tirar de letra qualquer operação.
Um dos maiores problemas na hora de um aluno aprender matemática é não relacionar o que está aprendendo com o seu cotidiano. Mas, com números decimais, não é bem assim.
Operações com Números Decimais
Imagina aquele momento em que você está pagando uma conta qualquer, seja no mercado, farmácia, ou até mesmo a passagem do ônibus. Após pagar com dinheiro, você confere o troco. É nesse momento que você precisa saber fazer operações com números decimais!
Nesta aula a seguir o professor Lucas te mostra como fazer operações com números decimais: adição, subtração, multiplicação e divisão.
Viu só que alua-show? Tudo bem simples e bem explicado. E você chega lá. E você pode fazer o Curso de Matemática Básica Gratuito, completo. Veja aqui o Resumão de Matemática Enem, só com o que mais cai nas provas. Inscrições abertas.
Dicas de Operações de Adição e Subtração
Exemplo: Para ser aprovado numa disciplina numa certa universidade, você precisa somar, nas três provas aplicadas, 21 pontos. Se você teve nota 7,4 na primeira, 8,33 na segunda, e 6 na terceira, você será aprovado?
Para somar ou diminuir números decimais basta colocar vírgula embaixo de vírgula e igualar as casas decimais completando-as com números zero. Após isso basta somar (diminuir) normalmente como se fossem números inteiros.Somando as notas das três provas: Como a soma foi maior do que 21, você pode se considerar aprovado.
Como a soma foi maior do que 21, você pode se considerar aprovado.
Operações de Multiplicação
Exemplo: O Pai de André propôs pagar-lhe R$ 3,45 por cada hora que ele se dedicasse estudando para as provas finais ao longo de uma semana. No fim desse período André somou suas horas de estudo e conclui que deu 20,3 horas. Dessa forma, quanto recebeu de seu pai?
Para multiplicar números decimais basta efetuar normalmente a operação fazendo de conta que as vírgulas não existem. Ao final, o número de casas decimais do produto é igual à soma dos números de casas decimais de cada fator.
Para calcular o valor recebido por André, basta multiplicar:
Aprenda a Divisão com números decimais
A dica da hora é você começar pelo resumo do professor Lucas Borguezan, do Curso Enem Gratuito. Em três minutos ele ensina como fazer a divisão com números decimais. Veja:
Exemplo: Ao passar no caixa de um supermercado, Antônio paga R$14,70 por um pacote de maçã cujo peso é de 4,2Kg. Quanto custa cada quilo dessa maçã?
Para efetuar a divisão de dois números decimais basta igualar o número de casas depois da vírgula (caso essas sejam diferentes) e abandonarmos as vírgulas. Em seguida dividimos normalmente como se fossem números naturais.
Voltando ao exemplo anterior, temos que dividir 14,70 por 4,2:
Portanto, cada quilo de maçã custa R$3,50.
Reforço Gratuito: como fazer contas com números decimais
Confira agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, as técnicas básicas para você transformar Frações en Números Decimais, e vice-versa.
Ficou mais fácil pra você aprender com as dicas do professor Sérgio Sarkis? Com certeza que sim. Bora avançar!
Transformação de Decimais em Frações
Decimais finitos
Observe que:
1) 7/10 = 0,7
2) 7/100 = 0,07
3) 7/1000 = 0,007
4) 216/100 = 2,16
Todo número cuja representação decimal for finita pode ser escrito na forma de uma fração com denominador 10, 100, 1000, etc.
O numerador da fração é o número inteiro que se obtém abandonando a vírgula e o denominador é formado pelo número 1 acrescido de tantos zeros quanto forem as casas após a vírgula do número fornecido.
Dica 1 – Matemática Enem – Aula sobre os critérios de divisibilidade em N
Como resolver Dízimas periódicas
Observe as divisões:
1) 5/9 = 0,55555….
2) 32/99 = 0,32323232…
3) 121/999 = 0,121121121…
Note que estes números têm uma representação decimal infinita e periódica e são chamados de dízimas periódicas simples. A fração que os representa (Fração Geratriz) tem como denominador números 9.
Podemos estabelecer a seguinte regra para dízimas periódicas simples: o numerador da fração geratriz será o número do período e o denominador será 9 ou 99 ou 999, etc…, ou seja, será formado por tantos nove quanto forem os algarismos do período.
Exemplos:
1) 0,454545… = 45/99
2) 0,761576157615… = 7615/9999
3) 0,222222… = 2/9
E se o número for, por exemplo, 2,3222222…. ou 0,43717171…?
Neste caso será chamado de dízima periódica composta e a sua transformação em fração pode ser feita da seguinte maneira:
Exemplos:
1) 2,3222222… =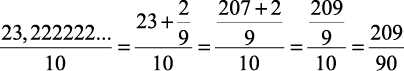
2) 0,43717171… =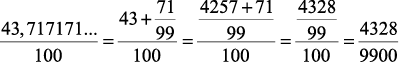
Exercício Resolvido
1) No tanque do seu carro cabem 50 litros de gasolina. Num certo momento, o marcador indica que ainda resta 1/4 do tanque. Se você quiser completar, quantos litros de gasolina deverá comprar? Se a gasolina custa R$2,58 o litro, quanto você pagará para completar o tanque?
Gabarito: 37,5 litros e R$ 96,75 para completar o tanque.
Dica 2 – Matemática Enem – Revisão sobre os Múltiplos e Divisores. Veja:
Simulado Enem de Matemática – Veja 10 questões sobre Regra de Três. Razão e Proporção, Frações e Cálculo de Área, de Volume, de Perímetro, e de Ângulos no Triângulo e na Circunferência. Acesse aqui o Simulado Enem de Matemática: 
Desafios sobre Frações e Números Decimais
Questão 1 – Operações com Números decimais
(Enem cancelado 2009) Três empresas de táxi W, K e L estão fazendo promoções: a empresa W cobra R$ 2,40 a cada quilômetro rodado e com um custo inicial de R$ 3,00; a empresa K cobra R$ 2,25 a cada quilômetro rodado e uma taxa inicial de R$ 3,80 e, por fim, a empresa L, que cobra R$ 2,50 a cada quilômetro rodado e com taxa inicial de R$ 2,80. Um executivo está saindo de casa e vai de táxi para uma reunião que é a 5 km do ponto de táxi, e sua esposa sairá do hotel e irá para o aeroporto, que fica a 15 km do ponto de táxi.
Assim, os táxis que o executivo e sua esposa deverão pegar, respectivamente, para terem a maior economia são das empresas
a) W e L. b) W e K. c) K e L.
d) K e W. e) K e K.
Questão 2
(Enem 2003) Os acidentes de trânsito, no Brasil, em sua maior parte são causados por erro do motorista. Em boa parte deles, o motivo é o fato de dirigir após o consumo de bebida alcoólica. A ingestão de uma lata de cerveja provoca uma concentração de aproximadamente 0,3 g/L de álcool no sangue.
A tabela a seguir mostra os efeitos sobre o corpo humano provocados por bebidas alcoólicas em função de níveis de concentração de álcool no sangue:
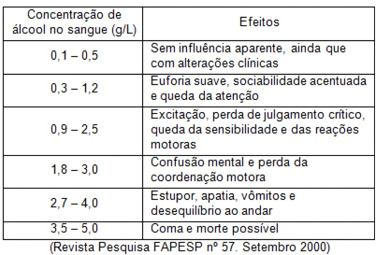
Uma pessoa que tenha tomado três latas de cerveja provavelmente apresenta
a) queda de atenção, de sensibilidade e das reações motoras.
b) aparente normalidade, mas com alterações clínicas.
c) confusão mental e falta de coordenação motora.
d) disfunção digestiva e desequilíbrio ao andar.
e) estupor e risco de parada respiratória.
Questão 3
(Enem 2009) A resolução das câmeras digitais modernas é dada em megapixels, unidade de medida que representa um milhão de pontos. As informações sobre cada um desses pontos são armazenadas, em geral, em 3 bytes. Porém, para evitar que as imagens ocupem muito espaço, elas são submetidas a algoritmos de compressão, que reduzem em até 95% a quantidade de bytes necessários para armazená-las. Considere 1 KB = 1.000 bytes, 1 MB = 1.000 KB, 1 GB = 1.000 MB.
Utilizando uma câmera de 2.0 megapixels cujo algoritmo de compressão é de 95%, João fotografou 150 imagens para seu trabalho escolar. Se ele deseja armazená-las de modo que o espaço restante no dispositivo seja o menor espaço possível, ele deve utilizar
a) um CD de 700 MB.
b) um pendrive de 1 GB.
c) um HD externo de 16 GB.
d) um memory stick de 16 MB.
e) um cartão de memória de 64 MB.
Dica 3 – Matemática Enem – Tudo sobre os números Naturais – https://blogdoenem.com.br/matematica-enem-numeros-naturais/
Questão 4
(Enem 1998) No quadro a seguir estão as contas de luz e água de uma mesma residência. Além do valor a pagar, cada conta mostra como calculá-lo, em função do consumo de água (em m3) e de eletricidade (em kWh). Observe que, na conta de luz, o valor a pagar é igual ao consumo multiplicado por um certo fator. Já na conta de água, existe uma tarifa mínima e diferentes faixas de tarifação.
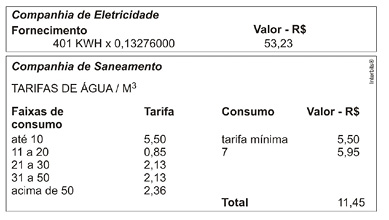
Suponha que dobre o consumo d’água. O novo valor da conta será de:
a) R$ 22,90 b) R$ 106,46 c) R$ 43,82 d) R$ 17,40 e) R$ 22,52
Questão 5 – Operações com Números Decimais
(UFES) Antônio compra abacaxis de um fornecedor ao preço de R$ 1,00 o lote de 3 unidades. Ele os revende na feira em amarrados com 5 unidades. Se o preço de cada amarrado é de R$ 2,00, quantos abacaxis deverá vender para ter um lucro de R$ 100,00?
a) 1.300 b) 1.400 c) 1.500
d) 1.600 e) 1.700
Você consegue resolver estes exercícios sobre as Operações com Números Decimais? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!


