Intervalos em R – Matemática Enem

Intervalos em R

• Nem toda solução de um problema matemático é um número.
• Muitas vezes essa solução é um conjunto numérico contido em  (conjunto dos reais).

Vamos ver a definição…

Considere dois números reais a e b, com a<b.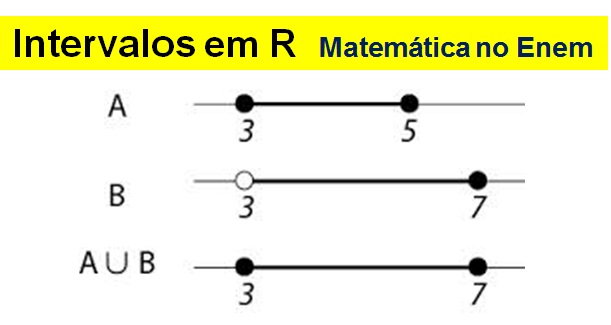 

I) Intervalo aberto de extremos a e b

• É o conjunto ]a,b[ = { x ∈ R / a < x < b }  .
• Além da representação ]a,b[  também utilizamos (a,b).
• Geometricamente representamos assim:
• 

Dica – Você notou que nesse intervalo as bolas que o representam são abertas? Sabe o que isso significa? 

Isso significa que os números representados no intervalo por a e b, não fazem parte da solução do problema!  Agora vamos ver um outro caso:

II) Intervalo fechado de extremos a e b

• É o conjunto [a,b] = { x ∈ R / a ≤  x  ≤ b }.
• Geometricamente representamos
• 

Dica do Blog – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas:  https://blogdoenem.com.br/category/cainaprova/matematica/ 

III) Intervalo fechado à esquerda e aberto à direita extremos a e b

• É o conjunto [a,b[ = { x ∈ R / a ≤  x  < b }.
• Geometricamente representamos
• 

IV) Intervalo aberto à esquerda e fechado à direita extremos ae b

• É o conjunto ]a,b] = { x ∈ R / a < x  ≤ b }.
• Geometricamente representamos
• 

V) Intervalos infinitos

a) ] -∞,b ] = { x ∈ R / x ≤ b }

b) ] -∞,b [ = { x ∈ R / x < b }

c) [ b, +∞ [ = { x ∈ R / x ≥ b }

d) ] b, +∞ [ = { x ∈ R / x > b }

Tipos de intervalos reais: Dados dois números reais p e q, chama-se intervalo a todo conjunto de todos os números reais compreendidos entre p e q, podendo inclusive incluir p e q.

Os números p e q são os limites do intervalo, sendo a diferença p – q, chamada amplitude do intervalo. Se o intervalo incluir p e q, o intervalo é fechado e caso contrário, o intervalo é dito aberto.

A tabela abaixo define os diversos tipos de intervalos:

Dica importante: (Tipos de notação para intervalos) – Notação de um intervalo na reta real com “bolinha fechada” – inclusão de termos, “bolinha aberta” – exclusão de termos, que também pode ser verificada através da notação de intervalos ou de conjuntos através dos colchetes (intervalo fechado) e colchetes invertido (intervalo aberto) e a notação algébrica de conjuntos,  como segue na imagem abaixo: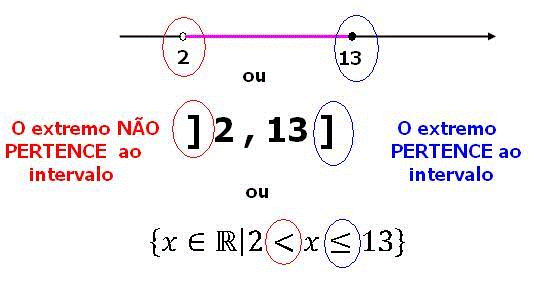

• Concluo a classificação dos intervalos com a seguinte pergunta para vocês:
• – E o intervalo vazio como seria definido?

Veja a Relação entre os Conjuntos Numéricos:

• O diagrama mostra a relação entre os conjuntos numéricos. Portanto, os números naturais, inteiros, racionais e irracionais são todos números reais. Como subconjuntos importantes de IR temos:
• IR* = IR-{0}
• IR₊ = conjunto dos números reais não negativos
• IR_ = conjunto dos números reais não positivos

Obs: Entre dois números inteiros existem infinitos números reais. Por exemplo:

• Entre os números 1 e 2 existem infinitos números reais:
• Entre os números 5 e 6 existem infinitos números reais:

5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 …

Dica 2 – Pronto para gabaritar na prova de matemática do Enem? Faça uma revisão com esta aula sobre Equações Polinomiais do 1º grau – https://blogdoenem.com.br/funcao-polinomial-matematica/

Saiba mais sobre os intervalos em R, assistindo a uma super videoaula onde o professor Nerckie explica as noções básicas sobre intervalos.

Vamos ver um exemplo para ficar mais fácil?

Suponha que seu intervalo para almoço comece às 12hs e termine às 14:00hs . Usando a linguagem matemática teríamos 3 formas de representação:

1a) Almoço = [12,14]

2a) Almoço = { x ∈ R / 12 ≤ x ≤ 14 }.

3a) Almoço = 

Dica 3 – Relembre outros assuntos de matemática acessando o nosso blog www.blogdoenem.com.br e gabarite as questões de matemática nas provas dos vestibulares e do Enem.

Os textos e exemplos de apresentação desta aula foram preparados pela professora Munique Dias para o Blog do Enem. Munique é formada em química pela UFSC, tem mestrado e atualmente cursa o doutorado em Engenharia. Química, também pela UFSC. Facebook: https://www.facebook.com/MuniqueDias .