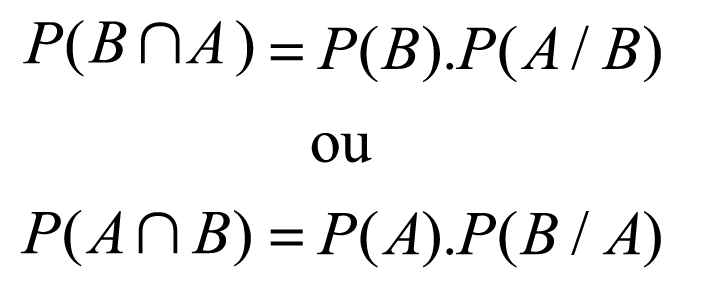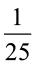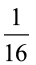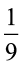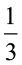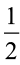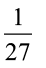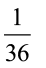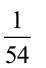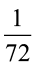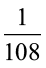Probabilidade & Estatística: resumo de Matemática Enem e vestibular

Para resolver problemas de probabilidade de um evento condicionado à ocorrência de um outro a estratégia para mandar bem é utilizar a famosa Probabilidade Condicional, cuja fórmula é dada por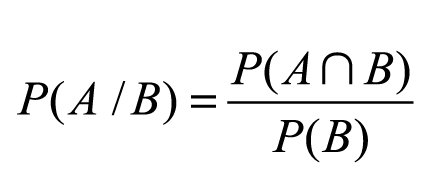em que P(A/B) representa a probabilidade de ocorrência do evento A, dado que já ocorreu B.

• Nesta fórmula, isolando P(A∩B), obtemos
• 
• que é equivalente a
• 

 

Observação importante:

1. Costumamos chamar essa fórmula de Regra do Produto
2. Quando a ocorrência do evento B afetar a probabilidade do evento A, dizemos que os eventos A e B são Dependentes. Quando não afetar, serão chamados de Independentes e, neste caso, a fórmula será dada por

 

Veja a seguir Exemplos de exercícios resolvidos bem típicos, que sempre caem, envolvendo jogo de dados e lançamentos de moedas para tirar no “cara ou coroa”. Se liga: 

01 – Lançando simultaneamente um dado e uma moeda, qual a probabilidade de obtermos o número 4 no dado e “cara” na moeda?

Resolução

Considere os eventos:

• A: número 4 no dado ⇒ P(A) = 1/6
• B: cara na moeda ⇒ P(B) = 1/2.

Queremos calcular P(A∩B). Pela fórmula,

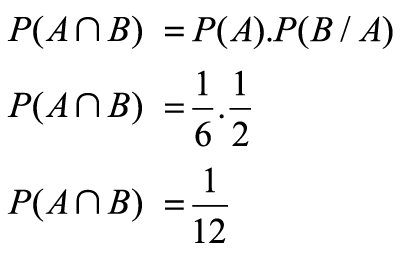
Perceba que o fato de ter saído cara na moeda não altera a probabilidade de sair o número 4 no dado. Logo, são eventos independentes.

Aula Gratuita sobre Probabilidade

Veja um resumo online completo com o professor Sérgio Sarkis, do canal Curso Enem Gratuito. Com ele você aprende fácil e manda bem no Enem:

 

Exemplo 02 – Exercício sobre Probabilidade e Estatística

Uma urna contém 10 bolas, sendo 3 azuis e 7 roxas. Retirando-se 2 bolas, uma após a outra, sem reposição, qual a probabilidade de que sejam ambas azuis?

Resolução

Considere os eventos:

• A: primeira bola azul
• B: segunda bola azul

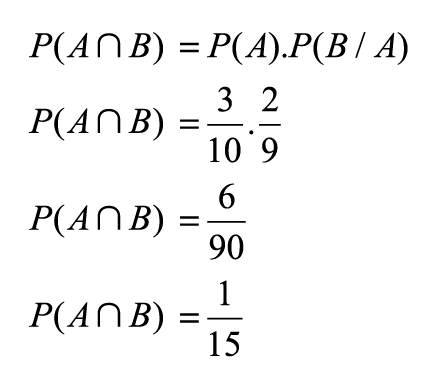
Note que aqui os eventos são dependentes, porque a probabilidade de a segunda ser também azul foi alterada pelo fato de a primeira já ter sido azul.

Simulado Enem de Probabilidade & Estatística

Resolva agora 10 questões do Simulado Enem com foco em exercícios de Probabilidade e Estatística. O Gabarito sai na hora. Veja aqui o Simulado:

 

Probabilidade – Simulado Enem

Dica 1 – Que tal revisar sobre Análise Combinatória? Aproveite esta aula e fique preparado para a prova de Matemática Enem. Estude com a gente para o Exame! – https://blogdoenem.com.br/analise-combinatoria-1-matematica-enem/

Saiba mais sobre Probabilidade nesta aula do canal Clube do Enem, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!

Desafios

Questão 01

Lançando-se duas moedas, qual a probabilidade de obtermos 2 coroas?

a) 10%

b) 15%

c) 20%

d) 25%

e) 30%

Dica 2 – Fique preparado para a prova de Matemática Enem com esta segunda aula sobre Análise Combinatória. Revise com a gente e garanta sua nota nas provas do Exame – https://blogdoenem.com.br/analise-combinatoria-2-matematica-enem/

Questão 02

Retiramos 3 bolas simultaneamente de uma urna contendo 10 bolas, sendo 4 azuis e 6 brancas. Qual a probabilidade de que as 3 sejam azuis?

a) 1/30

b) 7/30

c) 1/15

d) 3/20

e) 7/20

Dica 3 – Relembre sobre Progressão Geométrica em mais esta aula de revisão para a prova de Matemática Enem. Estude com a gente para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/progressao-geometrica-matematica-enem/

Questão 03

(Enem) Em um determinado semáforo, as luzes completam um ciclo de verde, amarelo e vermelho em 1 minuto e 40 segundos. Desse tempo, 25 segundos são para a luz verde, 5 segundos para a amarela e 70 segundos para a vermelha. Ao se aproximar do semáforo, um veículo tem uma determinada probabilidade de encontrá-lo na luz verde, amarela ou vermelha. Se essa aproximação for de forma aleatória, pode-se admitir que a probabilidade de encontrá-lo com uma dessas cores é diretamente proporcional ao tempo em que cada uma delas fica acesa.

Suponha que um motorista passa por um semáforo duas vezes ao dia, de maneira aleatória e independente uma da outra. Qual é a probabilidade de o motorista encontrar esse semáforo com a luz verde acesa nas duas vezes em que passar?

a)
b)
c)
d)
e)

Questão 04

(Enem 2005) Um aluno de uma escola será escolhido por sorteio para representá-la em uma certa atividade. A escola tem dois turnos. No diurno há 300 alunos, distribuídos em 10 turmas de 30 alunos. No noturno há 240 alunos, distribuídos em 6 turmas de 40 alunos.

Em vez do sorteio direto envolvendo os 540 alunos, foram propostos dois outros métodos de sorteio:

Método I: escolher ao acaso um dos turnos (por exemplo, lançando uma moeda) e, a seguir, sortear um dos alunos do turno escolhido.

Método II: escolher ao acaso uma das 16 turmas (por exemplo, colocando um papel com o número de cada turma em uma urna e sorteando uma delas) e, a seguir, sortear um dos alunos dessa turma.

Sobre os métodos I e II de sorteio é correto afirmar:

a) em ambos os métodos, todos os alunos têm a mesma chance de serem sorteados.

b) no método I, todos os alunos têm a mesma chance de serem sorteados, mas, no método II, a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.

c) no método II, todos os alunos têm a mesma chance de serem sorteados, mas, no método I, a chance de um aluno do diurno ser sorteado é maior que a de um aluno do noturno.

d) no método I, a chance de um aluno do noturno ser sorteado é maior do que a de um aluno do diurno, enquanto no método II ocorre o contrário.

e) em ambos os métodos, a chance de um aluno do diurno ser sorteado é maior do que a de um aluno do noturno.

Questão 05

(Enem 2001) Uma empresa de alimentos imprimiu em suas embalagens um cartão de apostas do seguinte tipo:

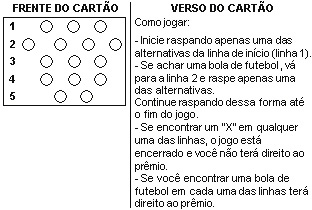
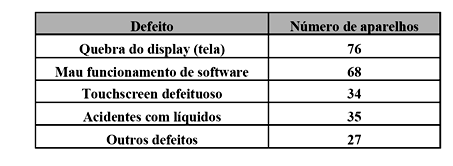
Cada cartão de apostas possui 7 figuras de bolas de futebol e 8 sinais de “X” distribuídos entre os 15 espaços possíveis, de tal forma que a probabilidade de um cliente ganhar o prêmio nunca seja igual a zero. Em determinado cartão existem duas bolas na linha 4 e duas bolas na linha 5. Com esse cartão, a probabilidade de o cliente ganhar o prêmio é

a)
b)
c)
d)
e)

Questão 06

(Enem) Em um concurso de televisão, apresentam-se ao participante três fichas voltadas para baixo, estando representadas em cada uma delas as letras T, V e E. As fichas encontram-se alinhadas em uma ordem qualquer. O participante deve ordenar as fichas a seu gosto, mantendo as letras voltadas para baixo, tentando obter a sigla TVE. Ao desvirá-las, para cada letra que esteja na posição correta ganhará um prêmio de R$200,00.

A probabilidade de o PARTICIPANTE não ganhar qualquer prêmio é igual a:

a) 0

b) 1/3

c) 1/4

d) 1/2

e) 1/6

Questão 07

(Enem) Um casal decidiu que vai ter 3 filhos. Contudo, quer exatamente 2 filhos homens e decide que, se a probabilidade fosse inferior a 50%, iria procurar uma clínica para fazer um tratamento específico para garantir que teria os dois filhos homens.

Após os cálculos, o casal concluiu que a probabilidade de ter exatamente 2 filhos homens é

a) 66,7%, assim ele não precisará fazer um tratamento.

b) 50%, assim ele não precisará fazer um tratamento.

c) 7,5%, assim ele não precisará fazer um tratamento.

d) 25%, assim ele precisará procurar uma clínica para fazer um tratamento.

e) 37,5%, assim ele precisará procurar uma clínica para fazer um tratamento.

Questão 08

(Enem 2010) A figura I abaixo mostra um esquema das principais vias que interligam a cidade A com a cidade B. Cada número indicado na figura II representa a probabilidade de pegar um engarrafamento quando se passa na via indicada,

Assim, há uma probabilidade de 30% de se pegar engarrafamento no deslocamento do ponto C ao o ponto B, passando pela estrada E4, e de 50%, quando se passa por E3. Essas probabilidades são independentes umas das outras.

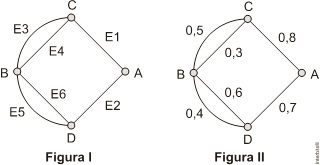
Paula deseja se deslocar da cidade A para a cidade B usando exatamente duas das vias indicadas, percorrendo um trajeto com a menor probabilidade de engarrafamento possível.

O melhor trajeto para Paula é

a) E1E3.

b) E1E4.

c) E2E4.

d) E2E5.

e) E2E6.