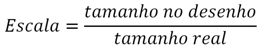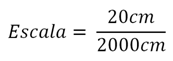Aprenda agora os fundamentos e o cálculo de Razão e Proporção. Com o domínio desta competência você também resolve questões de Escalas. Veja no resumo gratuito:
Todo ano você encontra muitas questões que envolvem o cálculo de Escalas, Razão e Proporção nas provas. São conteúdos muito comuns no Enem e em todos os vestibulares.
E, estes temas caem não só nas questões de matemática e física, mas também nas de geografia, química e biologia. Afinal, a Razão pode ser aplicada para resolver diversos tipos de problemas. Escalas acontecem direto nas questões de Geografia, sobre Escalas Cartográficas.
Cálculo de Escalas, Razão e Proporção
Então, dominar este fundamento da Matemática é básico para você conseguir ter um bom desempenho em todas as áreas que envolvem raciocínio lógico e cálculos simples de matemática.
O tema das Escalas também faz parte dos conteúdos clássicos da Matemática. Veja abaixo nossa explicação para mandar bem nas provas.
Como calcular Escalas
Veja agora no resumo com o professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Muito boa a explicação do professor Lucas. Confira agora Razão e Proporção.
Muitas vezes o cálculo sobre razão pode ser organizado em regra-de-três, como você pode ver no exemplo final deste post.
Vamos lá? O melhor começo é pela conceituação e o cálculo de Razão.
O que é a Razão
A razão entre dois números é simplesmente o quociente entre eles. Por exemplo, queremos saber a razão entre o número de meninos e meninas em uma sala de aula. Se há 12 meninos e 18 meninas, então a razão entre eles é 12/18. Você pode pronunciar “doze sobre dezoito”, ou então pode dizer “doze por dezoito”.
Veja como fazer o cálculo da Razão: Simplificando esta fração por 6, encontramos 2/3, ou seja, para cada 2 meninos há três meninas.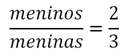
E você pode dizer “dois por três”, “dois sobre três”, ou dizer “dois terços”.
O que são as Escalas
Quando se constrói uma escala o costume é primeiro fazer uma planta, que contém o traçado, o desenho do que será construído. E, nesta planta devem estar consideradas e indicadas as medidas no tamanho real do que você quer representar.
E, na mesma planta, devem constar as medidas, o tamanho da figura desenhada, da planta. Estes tamanhos “do desenho na planta”, e da real dimensão do que será construido devem estar na mesma unidade de medida. 
Por exemplo, uma casa que possui um comprimento de 20 metros pode ser representada em um desenho em que a representação do comprimento da casa tem 20 cm. Vemos que as unidades de medida não são as mesmas.
Temos a casa em 20 metros, e a dimensão da casa na planta em 20 centímetros. Para resolver esta discrepância, portanto, vamos ter que transformar o metro em cm, pois é nesta unidade que representaremos o desenho, 20 metros = 2000 centímetros. Esta relação vai definir a Escala da Planta.
Veja o cálculo de Razão e Proporção
- A escala é simplesmente a razão entre o tamanho do desenho e o tamanho real, assim, para o nosso exemplo:
Simplificando por 20 o numerador e o denominador, e também a unidade de medida, encontramos a escala: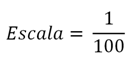
Ela significa que cada centímetro no desenho representa 100 centímetros no real. Você pode pronunciar que a escala é de “um para cem”. Ou seja, para cada “um centímetro” na planta, você tem “cem centímetros” na construção real.
Introdução à Razão e Proporção
Veja agora com o professor Sérgio Sarkis uma introdução perfeita ao estudo e resolução de questões do Enem envolvendo o cálculo de Razão e Proporção.
Mandou bem o professor Sérgio. Têm mais aulas com ele no canal de aulas do Curso Enem Gratuito. Veja agora os exercícios resolvidos de Proporção:
Resumo de Proporção & Regra de Três
Entenda o que são as Proporções – Esta habilidade matemática relacionada às proporções é muito cobrada no Enem e nos vestibulares. Dominá-la é garantir pontos para o seu sucesso. Para você compreender bem, vamos voltar ao exemplo inicial da quantidade de meninos e meninas em uma sala de aula citado anteriormente.
Vimos que a razão entre o número de meninos e meninas era de 2/3 (dois terços).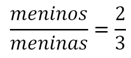
Vamos supor que o número de meninos e meninas cresça obedecendo esta mesma razão. Dizemos então que a nova quantidade estará na mesma proporção. Sendo assim, se o número de meninas agora é 9 qual será o número de meninos?
Se a razão é a mesma, podemos montar a seguinte relação para chegar ao resultado: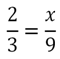
Este tipo de problema também é conhecido como regra-de-três e resolvemos igualando os produtos do numerador e uma fração pelo denominador da outra.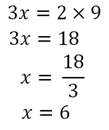
Ou seja, agora temos 6 meninos. Poderíamos pensar também do seguinte modo: se o número de meninas triplicou, então ou número de meninos também deve triplicar.
Resumo completo: Escalas, Razão e Proporção, e Regra de Três:
Confira com o professor Vinny, do canal Curso Enem Gratuito uma explicação bem didática e os macetes para você resolver os exercícios sobre Regra de Três, Razão & Proporção, e sobre Escala:
Mandou bem. Você encontra mais aulas no canal do Curso Enem Gratuito no Youtube.
Simulado Enem de Razão e Proporção:
Teste agora seus conhecimentos em 10 questões online. O gabarito sai na hora, e você ganha aulas de reforço para as questões que não acertar. Acesse o Simulado de Matemática Enem abaixo:
Exercícios: Expanda seus conhecimentos aqui através dos exercícios de Razões, proporções e taxas da Khan Academy.
Revisão gratuita de Regra de Três. Clique aqui.
Desafios para você resolver e compartilhar a solução:
1) (ENEM 2013) Em um certo teatro, as poltronas são divididas em setores. A figura apresenta a vista do setor 3 desse teatro, no qual as cadeiras escuras estão reservadas e as claras não foram vendidas.
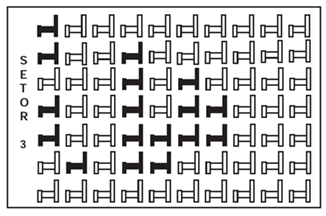
A razão que representa a quantidade de cadeiras reservadas do setor 3 em relação ao total de cadeiras desse mesmo setor é
A) 17/10 B) 17/53 C) 53/70 D) 53/17 E) 70/17
2) (ENEM 2013) Para se construir um contrapiso, é comum, na constituição do concreto, se utilizar cimento, areia e brita, na seguinte proporção: 1 parte de cimento, 4 partes de areia e 2 partes de brita. Para construir o contrapiso de uma garagem, uma construtora encomendou um caminhão betoneira com 14 m3 de concreto.
Qual é o volume de cimento, em m3, na carga de concreto trazido pela betoneira?
A) 1,75 B) 2,00 C) 2,33 D) 4,00 E) 8,00
Gabarito:
1)A; 2) B
Autoria do professor Alexsandro Sunaga – https://www.facebook.com/
Este post é resultado da parceria da Fundação Lemann com o Blog do Enem – www.fundacaolemann.org.br.
