O estudo das Relações prepara você para o estudo das ‘Funções’, além disso, vai ajudá-lo nas provas de matemática do Enem e dos Vestibulares. As Relações são utilizadas também no estudo de números e dos conjuntos.
RELAÇÕES
Você utiliza o conceito de “relação” todos os dias, e muitas vezes sem nem perceber. Por exemplo, quando você diz que fulano é primo de sicrano, você utilizou uma ‘relação’.
Outro exemplo de “relação” é quando você diz que um carro é maior que o outro, ou que é mais veloz do que o outro.
O que é Relação na matemática? – Como o próprio nome sugere, temos uma relação quando estabelecemos uma correspondência entre dois objetos (números, conjuntos, matrizes e etc.). Esta correspondência pode ser definida através de uma regra (lei) ou não.
Quando esta relação é feita através de uma lei fica fácil observar se dois objetos estão ou não associados. Por exemplo: maior do que é uma associação que esta definida no conjunto dos números naturais:
7 > 3
Neste caso, 7 esta relacionado com 3, pois sete é maior do que três. Já 7 não está relacionado com 15, pois 7 não é maior do que 15.
Dica 1 – Quer recuperar oconteúdo de Regra de Três? Sempre ajuda na resolução de problemas. Veja aqui uma aula especial sobre Regra de Três: https://blogdoenem.com.br/regra-de-tres-matematica/
Alguns pares de números naturais relacionados através da relação maior do que são: (4, 3), (27, 20), (35, 34). Lembrando-se da noção de Pares Ordenados, 15 não esta relacionado com 25, mas 25 esta relacionado com 15.
De acordo com o exposto acima podemos estabelecer a seguinte definição:
Sejam A e B dois conjuntos. Uma relação R de A em B é um subconjunto de .
Compreendeu? Saiba mais sobre relações assistindo a esta videoaula do Professor Edir Bessa, do colégio Cascavelense. Como você já sabe, cai direto no Enem e no vestibular, e vale para outras matérias também:
Dica 2 – Você sabe o que é e como calcular um Produto Cartesiano? Faça aqui uma revisão em dez minutos. É um fundamento importante para você aprender sobre Funções: https://blogdoenem.com.br/produto-cartesiano/
Agora, aprenda sobre Domínio, Contradomínio, e Imagem de uma Relação.
Definição: Dada uma relação R de A em B chama-se domínio de R aos primeiros elementos dos pares pertencentes a R, ou seja, os elementos x que pertence a A, tal que e . Chama-se Contradomínio de R ao conjunto B. E, chama-se Imagem de R aos segundos elementos dos pares ordenados de R, ou seja, os elementos y que pertencem a B, tal que e .
Observações: Denotamos o domínio de R por D(R), o contradomínio de R por C(R), e a imagem de R por I(R) ou Im(R). D(R) é subconjunto de A e Im(R) é subconjunto de B.
Dica 3 – Saiba mais sobre relações assistindo a vídeo aula totalmente gratuita da Khan Academy traduzida para o português pela Fundação Lemann e mande bem nas questões de matemática dos vestibulares e também do Enem. http://www.fundacaolemann.org.br/khanportugues/matematica/algebra/graficos_e_analises_de_funcoes_lineares/tracando_relacoes_de_x_y
Relações no plano.
Primeiro devemos lembrar que uma relação R de A em B é um subconjunto do produto cartesiano , ou seja, , quando A e B são subconjunto de podemos representa esta relação num plano cartesiano de ℝ×ℝ (lembre-se da aula sobre produto cartesiano para fazer a representação gráfica de certas relações), observe:
1)![]()
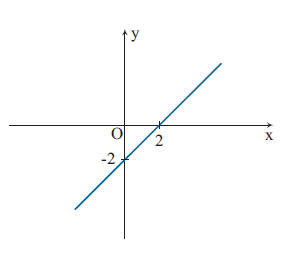
2) ![]()
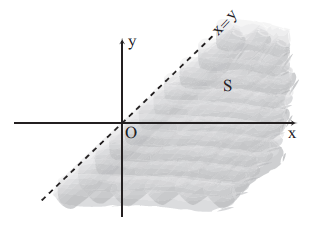
Dica 4 – O que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas https://blogdoenem.com.br/category/cainaprova/matematica/
Exercício: (Enem 2010) – Uma torneira gotejando diariamente é responsável por grandes desperdícios de agua. Observe o gráfico que indica o desperdício de uma torneira:
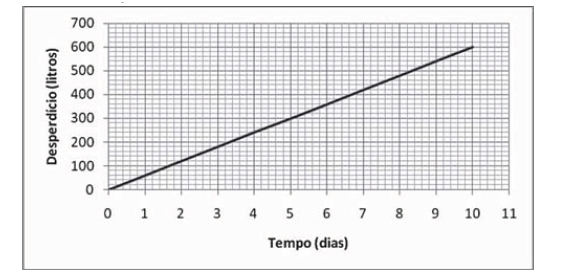
Se y representa o desperdício de agua, em litros, e x representa o tempo, em dias, a relação entre x e y é:
a) y = 2x
b) y = (1/2)x
c) y = 60x
d) y = 60x + 1
e) y = 80x + 50
Resposta: No gráfico acima, notamos facilmente que dois pares desta relação são: (5, 300) e (10, 600). Por outro lado, se y esta em função de x, então podemos escrever esta relação como sendo . Desta forma, basta descobrirmos o valor de a substituindo os dois pares na relação, observe:
Multiplicando os dois lados da segunda igualdade por -1 e fazendo a subtração teremos:
Logo, consequentemente a relação será . Portanto, a resposta correta é a alternativa C.
O texto acima foi preparado pelo professor Orlandino R. F. da Silva Junior para o Blog do Enem. Orlandino é formado em Matemática pela Universidade Federal de Santa Catarina – UFSC desde 2002. Skype: orfajr.
