Revise sobre a Segunda Lei da Termodinâmica: entenda porque uma máquina térmica funcionando em ciclos deve operar entre duas temperaturas constantes.
É hora de revisar a Segunda Lei da Termodinâmica. O princípio da conservação da energia estabelece que as conversões de energia de uma forma em outra devem ocorrer de modo que a energia total permaneça constante.
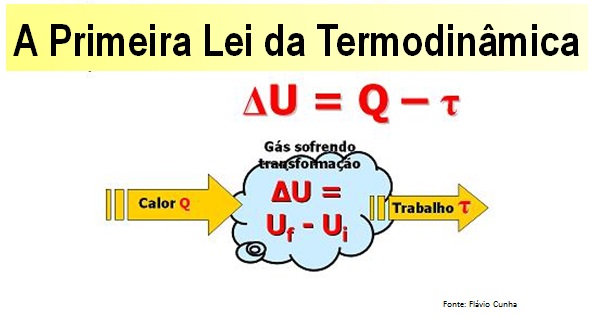
A primeira lei da termodinâmica, ΔU = Q – τ, é uma reafirmação desse princípio de conservação e, portanto, deve sempre ser obedecida. Entretanto, a primeira lei da termodinâmica não prevê a possibilidade da realização de um determinado processo, ou seja, nem todos os processos que obedecem à primeira lei da termodinâmica podem ser realizados na prática.
Já vimos que, para as máquinas térmicas e para as máquinas frigoríficas, respectivamente, calor é convertido em trabalho e trabalho é convertido em calor (figura a seguir).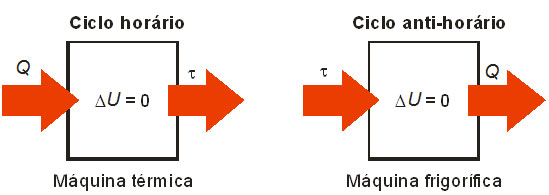
A representação acima, contudo, é uma simplificação, pois na máquina térmica, por exemplo, todo o calor está sendo convertido em trabalho, ou seja, a máquina representada tem um aproveitamento de 100% da energia recebida. Uma máquina térmica não pode converter em trabalho todo o calor recebido.
Na verdade, toda máquina térmica e toda máquina frigorífica deve obedecer à primeira lei da termodinâmica e também à segunda lei da termodinâmica.
Dica 1 – Saiba tudo sobre as Transformações Cíclicas dos gases em mais uma aula de revisão para a prova de Física Enem – https://blogdoenem.com.br/transformacao-ciclica-de-um-gas-fisica-enem/
Dica 2 – Relembre tudo sobre a Primeira Lei da Termodinâmica em mais esta aula preparatória para prova de Física Enem. Estude com a gente e fique preparado! – https://blogdoenem.com.br/primeira-lei-da-termodinamica-fisica-enem/ 
A segunda lei da termodinâmica tem um caráter estatístico e estabelece um sentido preferencial de ocorrência dos processos naturais.
Se levarmos em conta que calor é uma forma degradada de energia e que sua conversão em energia mecânica, por exemplo, não é integral como estabelecido pela primeira lei da termodinâmica, podemos enunciar a segunda lei da termodinâmica em outros termos:
É impossível a uma máquina térmica operando em ciclos converter integralmente calor em trabalho.
De acordo com a segunda lei da termodinâmica, uma máquina térmica funcionando em ciclos deve operar entre duas temperaturas constantes. A máquina recebe uma quantidade de calor Q1 de uma fonte quente, à temperatura mais alta T1, converte parte deste calor em trabalho útil τ e rejeita uma quantidade de calor Q2 para uma fonte fria, à temperatura mais baixa T2.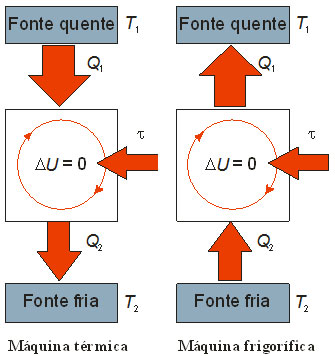
Dessa maneira, pelo princípio de conservação de energia e da primeira lei da termodinâmica, o trabalho útil τ é dado por: 
Dica 3 – O Exame Nacional do Ensino Médio está quase aí! Revise sobre Termodinâmica e garanta sua nota na prova de Física Enem – https://blogdoenem.com.br/termodinamica-fisica-enem-2/
Portanto, naquela representação anterior, estávamos representando por Q apenas a diferença entre o calor recebido da fonte quente e o calor rejeitado para a fonte fria.
Rendimento
Como nem toda energia recebida é convertida em trabalho, o ciclo térmico apresenta um rendimento 
definido como:
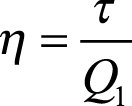
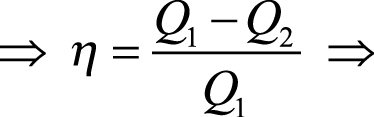
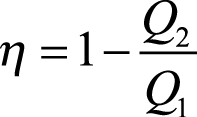
Como o trabalho útil τ é sempre menor que a quantidade de calor Q1, podemos enunciar a segunda lei da termodinâmica em outros termos:
Na prática, todas as máquinas térmicas cíclicas têm rendimento menor do que 100%.
Para as máquinas frigoríficas não calculamos o seu rendimento, mas sim a grandeza eficiência e, dada por:
O ciclo de Carnot
O ciclo de Carnot é um ciclo teórico proposto pelo físico, matemático e engenheiro francês Nicolas Léonard Sadi Carnot (1796-1832).
A importância do ciclo de Carnot reside no fato de este ciclo, ao operar entre as temperaturas T1 (fonte quente) e T2 (fonte fria), apresentar rendimento maior do que o de qualquer outro ciclo.
O ciclo de Carnot consta de duas transformações adiabáticas alternadas a duas transformações isotérmicas, como representado no diagrama p × V da figura a seguir.
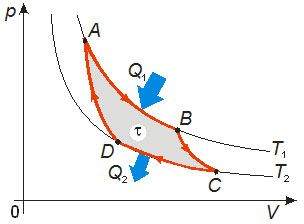
A → B é uma expansão isotérmica durante a qual o gás recebe a quantidade de calor Q1 da fonte quente.
B → C é uma expansão adiabática durante a qual o gás sofre o resfriamento e sua temperatura varia de T1 (temperatura da fonte quente) para T2 (temperatura da fonte fria).
C → D é uma compressão isotérmica durante a qual o gás rejeita a quantidade de calor Q2 para a fonte fria.
D → A é uma compressão adiabática durante a qual o gás sofre o aquecimento e sua temperatura varia de T2 (temperatura da fonte fria) para T1 (temperatura da fonte quente).
O rendimento de uma máquina térmica, como visto anteriormente, é dado por:
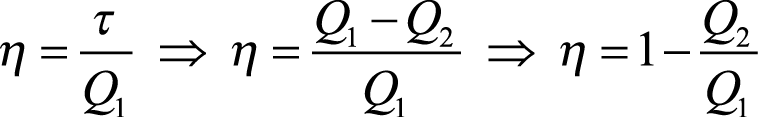
Para um ciclo de Carnot pode-se demonstrar que a quantidade de calor trocada pelo gás é diretamente proporcional à temperatura da fonte: 
Assim, o rendimento de uma máquina de Carnot é dado por:
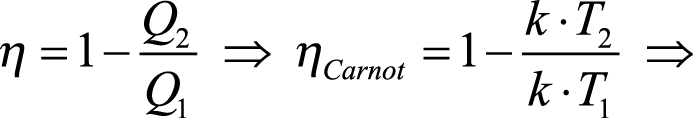
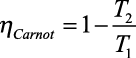
É importante ressaltar que o rendimento de um ciclo de Carnot é o máximo quando operando entre duas dadas fontes a temperaturas T1 e T2, mas nunca é igual a 100%.
Assim, podemos enunciar a segunda lei da termodinâmica em termos de temperatura.
Na prática, o zero absoluto (0 K) é inatingível.
Desafios
Questão 1
(CEFET – PR) O 2° princípio da Termodinâmica pode ser enunciado da seguinte forma: “É impossível construir uma máquina térmica operando em ciclos, cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho”. Por extensão, esse princípio nos leva a concluir que:
a) sempre se pode construir máquinas térmicas cujo rendimento seja 100%;
b) qualquer máquina térmica necessita apenas de uma fonte quente;
c) calor e trabalho não são grandezas homogêneas;
d) qualquer máquina térmica retira calor de uma fonte quente e rejeita parte desse calor para uma fonte fria;
e) somente com uma fonte fria, mantida sempre a 0°C, seria possível a uma certa máquina térmica converter integralmente calor em trabalho.
Questão 2
(EN–RJ) Um motor térmico recebe 1200 calorias de uma fonte quente mantida a 227°C e transfere parte dessa energia para o meio ambiente a 24°C. Qual o trabalho máximo, em calorias, que se pode esperar desse motor?
a) 552
b) 681
c) 722
d) 987
e) n.d.a.
Questão 3
(PUC–PR) Uma máquina térmica, operando em um ciclo de Carnot, trabalha entre as temperaturas de –73 °C e 227 °C. Em cada ciclo, a máquina recebe 500 J de calor da fonte quente.
Analise as seguintes afirmativas:
I. O rendimento dessa máquina é de 40%.
II. O trabalho realizado pela máquina é de 300 J.
III. O calor rejeitado, por ciclo, para a fonte fria é de 200J.
Está correta ou estão corretas:
a) I e II.
b) II e III.
c) I e III.
d) somente II.
e) somente III.
Questão 4
(UNAMA) Um motor de Carnot cujo reservatório à baixa temperatura está a 7,0 °C apresenta um rendimento de 30%. A variação de temperatura, em kelvins, da fonte quente a fim de aumentarmos seu rendimento para 50%, será de:
a) 400
b) 280
c) 160
d) 560
Questão 5
(UFV-MG) As afirmativas abaixo se referem à Segunda Lei da Termodinâmica:
I) Nenhuma máquina térmica que opere entre duas temperaturas dadas pode apresentar maior rendimento que uma máquina de Carnot que opere entre as mesmas temperaturas.
II) É impossível qualquer transformação cujo único resultado seja a absorção de calor de um reservatório a uma temperatura única e sua total conversão em trabalho mecânico.
III) Uma máquina de Carnot apresenta menor rendimento ao operar entre 10 ºC e -10 ºC do que ao operar entre 80 ºC e 60 ºC.
Dentre as afirmações anteriores, são verdadeiras:
a) I e II.
b) I, II e III.
c) I e III.
d) apenas a I.
e) II e III.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
