Matemática é sempre uma pedreira no Enem. Mas, tem questões que sempre caem e que não dá para errar. Veja revisão gratuita de Progressão Geométrica para gabaritar neste conteúdo. Aula gratuita com exemplos e exercícios.
Você tem o raciocínio rápido para resolver jogos ou problemas de Sequências ou de Progressão Geométrica? Por exemplo, se alguém lhe disser 3; 9; e 27; qual seria o próximo número?
Vamos lá revisar: Progressão Geométrica é toda sequência numérica com termos não nulos em que o quociente entre um termo e o seu antecedente é constante. A essa constante dá-se o nome de razão q da PG.
Complicou para você a definição? Vamos facilitar observando estes Exemplos. Considere aqui o Exemplo 01: PG (1, 2, 4, 8, 16, …).
Ficou fácil para você deduzir a solução, concorda? Se ainda não matou a charada, veja que há uma equivalência entre os termos. Veja na representação matemática: 2/1 = 4/2 = 8/4 = 16/8 = 2. Ou seja, o quociente constante na Progressão Geométrica é 2 (dois).
Antes de ver mais exemplos, assista à explicação do prof. Lucas do canal do Curso Enem Gratuito:
Mais um exemplo de Progressão Geométrica:
Observe a sequência e determine o quociente constante nesta Progressão Geométrica: PG (81, 27, 9, 3, 1, …). Acompanhe a resolução para você compreender o raciocínio: Aqui também temos quociente constante entre qualquer termo e seu antecedente. Você já sabe qual é ele? Veja como é simples para chegar à solução: 27/81 = 9/27 = 3/9 = 1/3 = q. Ou seja, cada termo está dividido por 3 (três) para chegar ao termo seguinte.
Outro exemplo:
PG (5, 5, 5, 5, …). Matou fácil este desafio, certo? É claro que neste caso o quociente constante da Progressão geométrica é q = 1. Uma dica importante: Esta sequência é chamada de constante e sempre será, além de PG de razão q = 1, uma PA de razão r = 0.
Propriedades da progressão Geométrica
Numa PG sempre se encontram as seguintes propriedades:
- P1) – O produto dos termos extremos é igual ao produto dos termos equidistantes dos extremos.
- P2) – O quadrado de um termo central é igual ao produto dos equidistantes dele.
Veja a confirmação dessas propriedades no exemplo abaixo:
PG (1, 2, 4, 8, 16, 32, 64)
P1) 1 . 64 = 2 . 32 = 4 . 16
P2)82 = 1 . 64 = 2 . 32 = 4 . 16
Fórmula do termo geral de uma PG
Supondo que o interesse seja obter o 13o termo da PG (1/4, 1/2, 1, 2, …), seria muito prático usar uma fórmula para obtê-lo, não é mesmo?
Vamos à fórmula:
Considere uma PG qualquer
P.G.(a1,a2,a3,a4,…,an,…)
Veja que:
a2 = a1 . q
a3 = a1 . q2
a4 = a1 . q3
E desse modo pode-se generalizaran = a1 . qn-1como a fórmula do termo geral de uma PG.
Voltando à pergunta “Qual o 13o da P.G. (1/4, 1/2, 1, 2,…)?”, temos que
a13 = a1 . q12
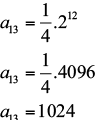
Fórmula da soma dos termos de uma PG:
PG finita:
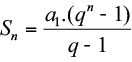
PG infinita (limite da soma dos termos):
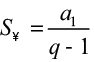
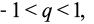
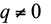
Exercícios de aplicação para você não esquecer Progressão Geométrica:
Exercício 01
Qual a razão da PG (x, x+2, x+16)?
Exercício 02
(CESGRANRIO, 1991) Um artigo custa hoje Cr$ 100,00 e seu preço é aumentado, mensalmente, em 12% sobre o preço anterior. Se fizermos uma tabela do preço desse artigo mês a mês, obteremos uma Progressão
a) Aritmética de razão 12.
b) Aritmética de razão 0,12.
c) Geométrica de razão 12.
d) Geométrica de razão 1,12.
e) Geométrica de razão 0,12.
Exercício 03
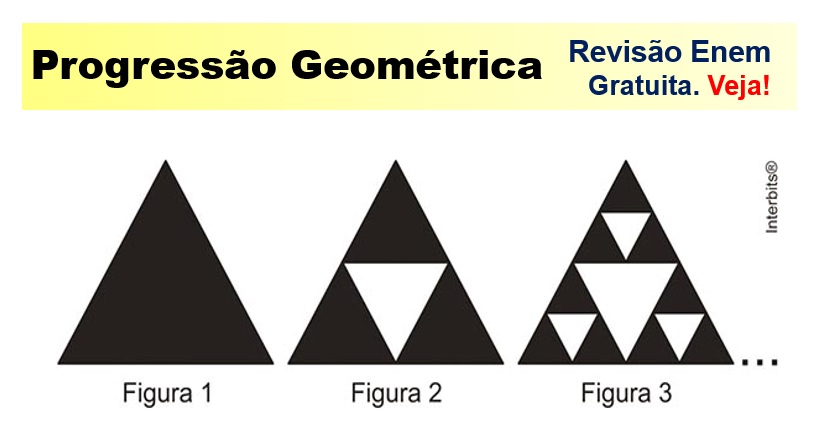
(ENEM, 2008) Fractal (do latim fractus, fração, quebrado) – objeto que pode ser dividido em partes que possuem semelhança com o objeto inicial. A geometria fractal, criada no século XX, estuda as propriedades e o comportamento dos fractais – objetos geométricos formados por repetições de padrões similares.
O triângulo de Sierpinski, uma das formas elementares da geometria fractal, pode ser obtido por meio dos seguintes passos:
1. Comece com um triângulo equilátero (Figura 1);
2. Construa um triângulo em que cada lado tenha a metade do tamanho do lado do triângulo anterior e faça três cópias;
3. Posicione essas cópias de maneira que cada triângulo tenha um vértice comum com um dos vértices de cada um dos outros dois triângulos, conforme ilustra a Figura 2;
4. Repita sucessivamente os passos 2 e 3 para cada cópia dos triângulos obtidos no passo 3 (Figura 3).
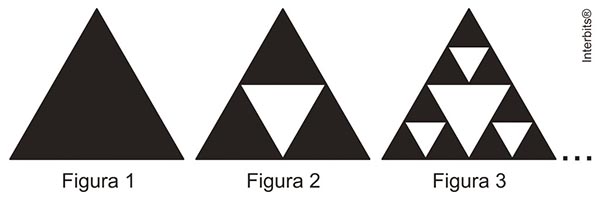
De acordo com o procedimento descrito, a Figura 4 da sequência apresentada acima é
|
a) |
|
|
b) |
|
|
c) |
|
|
d) |
|
|
e) |
|
Desafios
Questão 01
(UDESC, 2011) Em uma escola com 512 alunos, um aluno apareceu com o vírus do sarampo. Se esse aluno permanecesse na escola, o vírus se propagaria da seguinte forma: no primeiro dia, um aluno estaria contaminado; no segundo, dois estariam contaminados; no terceiro, quatro, e assim sucessivamente. A diretora dispensou o aluno contaminado imediatamente, pois concluiu que todos os 512 alunos teriam sarampo no:
a) 9º dia
b) 10º dia
c) 8º dia
d) 5º dia
e) 6º dia
Dica 1 – Fique preparado para prova de Matemática Enem acompanhando esta aula sobre de revisão sobre Progressão Aritmética – https://blogdoenem.com.br/progressao-aritmetica-aula-de-revisao-para-matematica-enem/
Questão 02
(UEL, 2009) “Thomas Malthus (1766-1834) assegurava que, se a população não fosse de algum modo contida, dobraria de 25 em 25 anos, crescendo em progressão geométrica, ao passo que, dadas as condições médias da Terra disponíveis em seu tempo, os meios de subsistência só poderiam aumentar, no máximo, em progressão aritmética.”
A lei de Malthus cita progressões aritméticas (PA) e progressões geométricas (PG).
Se os dois primeiros termos de uma sequência são x1 = 6 e x2 = 12, o quinto termo será:
a) x5 = 16, se for uma PA, e x5 = 24, se for uma PG.
b) x5 = 24, se for uma PA, e x5 = 96, se for uma PG.
c) x5 = 30, se for uma PA, e x5 = 30, se for uma PG.
d) x5 = 30, se for uma PA, e x5 = 96, se for uma PG.
e) x5 = 48, se for uma PA, e x5 = 72, se for uma PG.
Dica 2 – Você já estudou sobre juros simples e juros compostos? Revise tudo sobre cálculo de porcentagem e juros em mais uma aula de Matemática Enem – https://blogdoenem.com.br/porcentagem-juros-simples-e-compostos-matematica-enem/
Questão 03
(UFSM, 2008) Uma fábrica vendia 12 camisetas por mês para certa rede de academias desde janeiro de um determinado ano. Devido ao verão, essa venda foi triplicada a cada mês, de setembro a dezembro. O total de camisetas vendidas nesse quadrimestre e a média de vendas, por mês, durante o ano, foram, respectivamente,
a) 1.536 e 128
b) 1.440 e 128
c) 1.440 e 84
d) 480 e 84
e) 480 e 48
Dica 3 – Já sabe tudo sobre cálculo de porcentagem? Que tal dar mais uma revisada com esta aula e ficar preparado para a prova de Matemática Enem? – https://blogdoenem.com.br/aula-de-porcentagem-revisao-de-matematica-enem/
Questão 04
(UFF, 2010) Com o objetivo de criticar os processos infinitos utilizados em demonstrações matemáticas de sua época, o filósofo Zenão de Eleia (século V a.C.) propôs o paradoxo de Aquiles e a tartaruga, um dos paradoxos mais famosos do mundo matemático.

Existem vários enunciados do paradoxo de Zenão. O escritor argentino Jorge Luis Borges o apresenta da seguinte maneira:
“Aquiles, símbolo de rapidez, tem de alcançar a tartaruga, símbolo de morosidade. Aquiles corre dez vezes mais rápido que a tartaruga e lhe dá dez metros de vantagem. Aquiles corre esses dez metros, a tartaruga corre um; Aquiles corre esse metro, a tartaruga corre um decímetro; Aquiles corre esse decímetro, a tartaruga corre um centímetro; Aquiles corre esse centímetro, a tartaruga um milímetro; Aquiles corre esse milímetro, a tartaruga um décimo de milímetro, e assim infinitamente, de modo que Aquiles pode correr para sempre, sem alcançá-la.”
Fazendo a conversão para metros, a distância percorrida por Aquiles nessa fábula é igual a:
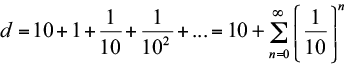
É correto afirmar que:
a) d = + ∞
b) d = 11,11
c) d =
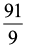
d) d = 12
e) d =
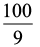
Questão 05
(UNEMAT, 2010) Lança-se uma bola, verticalmente de cima para baixo, da altura de 4 metros. Após cada choque com o solo, ela recupera apenas metade da altura anterior.
A soma de todos os deslocamentos (medidos verticalmente) efetuados pela bola até o momento de repouso é:
a) 12 m
b) 6 m
c) 8 m
d) 4 m
e) 16 m
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!








