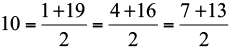O Exame Nacional do Ensino Médio está na sua agenda! Relembre aqui sobre Progressão Aritmética nesta aula de revisão para a prova de Matemática Enem. Veja abaixo.
Você está em dia com a Progressão Aritmética, a ‘conhecida’ PA? Se ainda não, é hora de pegar as melhores dicas aqui.
Mas, se você já domina PA, mesmo assim o Blog recomenda que você faça uma revisão. Nem que seja apenas para você ter certeza de que vai mandar bem nas questões de Matemática no Enem.
Conceito de Progressão Aritmética:
Progressão Aritmética é toda sequência numérica em que a diferença entre um termo e o seu antecedente é constante.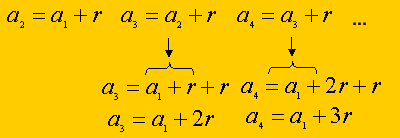 A essa constante dá-se o nome de razão r da PA.
A essa constante dá-se o nome de razão r da PA.
- Veja nestes Exemplos:
- Exemplo 01: PA (1, 5, 9, 13, 17, …)
- Veja que 5-1 = 9-5 = 13-9 = 17-13 = 4 = r
- Exemplo 02: PA (20, 18, 16, 14, …)
- Aqui também há diferença constante entre qualquer termo e seu antecedente. Veja:
- 18-20 = 16-18 = 14-16 = -2 = r
- Exemplo 03: PA (5, 5, 5, 5, …)
- Neste caso, r = 0.
Assim, pode-se elaborar a seguinte classificação:
• PA Crescente ⇒ r > 0
• PA Decrescente ⇒ r < 0
• PA Constante ⇒ r = 0
Numa PA sempre se encontram as seguintes propriedades:
• P1) A soma dos termos extremos é igual à soma dos termos equidistantes dos extremos.
• P2) Um termo central é igual à média aritmética dos equidistantes.
Veja a confirmação dessas propriedades no exemplo abaixo:
- PA (1, 4, 7, 10, 13, 16, 19)
- P1) 1+19 = 4 +16 = 7+13
- P2)

Veja a aula do prof. Lucas do Curso Enem Gratuito para entender ainda melhor o conteúdo:
Dica 1 – Você já estudou sobre juros simples e juros compostos? Revise tudo sobre cálculo de porcentagem e juros em mais uma aula de Matemática Enem – https://blogdoenem.com.br/porcentagem-juros-simples-e-compostos-matematica-enem/
Fórmula do termo geral de uma PA
Supondo que nosso interesse seja obter o 51o da PA (2, 5, 8, …), seria muito prático usar uma fórmula para obtê-lo, não é mesmo?
Utilizar uma fórmula já consagrada para resolver problemas de Progressão Aritmética pode parecer simples. De fato, na conta matemática não tem complicação. O essencial é você ler e compreender a questão para saber como encaixar na fórmula os termos para resolver a questão. Um algarismo fora de lugar, e… já era o resultado.
Vamos à fórmula clássica: an=a1 +(n-1).r
- Considere uma PA qualquer
- P.A.(a1,a2,a3,a4, …, an, …)
- Veja que:
- a2 = a1 + r
- a3 = a1 + 2r
- a4 = a1 + 3r
Desse modo, pode-se generalizar como a fórmula do termo geral de uma PA.
- Voltando à pergunta “Qual o 51o da PA (2, 5, 8, …)?”, observe que
- a51 = a1 + 50r
- a3 = 2 + 50.3
- a4 = 152
Dica 2 – Já sabe tudo sobre cálculo de porcentagem? Que tal dar mais uma revisada com esta aula e ficar preparado para a prova de Matemática Enem? – https://blogdoenem.com.br/aula-de-porcentagem-revisao-de-matematica-enem/
Fórmula da soma dos termos de uma PA:
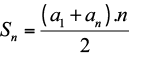
Exercícios de aplicação
Exercício 01
Qual a razão da PA (x-2, 2x-3, x+8)?
Exercício 02
(ENEM) O número mensal de passagens de uma determinada empresa aérea aumentou no ano passado nas seguintes condições: em janeiro foram vendidas 33.000 passagens; em fevereiro, 34.500; em março, 36.000. Esse padrão de crescimento se mantém para os meses subsequentes.
Quantas passagens foram vendidas por essa empresa em julho do ano passado?
a) 38 000
b) 40 500
c) 41 000
d) 42 000
e) 48 000
Dica 3 – Você lembra como funcionam a Regra de Três Simples e a Regra de Três Composta? Revise com esta aula de Razões e Proporções para a prova de Matemática Enem – https://blogdoenem.com.br/razoes-e-proporcoes-matematica-enem/
Exercício 03
(UFPB) Na organização de um determinado rali, quanto à quilometragem diária a ser percorrida pelas equipes participantes durante os 20 dias da competição, ficou estabelecida a seguinte regra: no primeiro dia, as equipes deveriam percorrer 500 km, e nos dias subsequentes deveriam percorrer 20 km a mais que no dia anterior.
A partir dos dados apresentados, é correto afirmar que uma equipe, para completar a prova, deverá percorrer no mínimo:
- a) 14.000 km
- b) 13.800 km
- c) 13.600 km
- d) 13.400 km
- e) 13.200 km
Quer dar um salto de aprendizagem? Veja também a Progressão Geométrica
Muito bom este resumo!!!
Desafios de Progressão Aritmética
Questão 01
(ENEM, 2ª aplicação, 2010) Nos últimos anos, a corrida de rua cresce no Brasil. Nunca se falou tanto no assunto como hoje, e a quantidade de adeptos aumenta progressivamente, afinal, correr traz inúmeros benefícios para a saúde física e mental, além de ser um esporte que não exige um alto investimento financeiro.
Um corredor estipulou um plano de treinamento diário, correndo 3 quilômetros no primeiro dia e aumentando 500 metros por dia, a partir do segundo. Contudo, seu médico cardiologista autorizou essa atividade até que o corredor atingisse, no máximo, 10 km de corrida em um mesmo dia de treino. Se o atleta cumprir a recomendação médica e praticar o treinamento estipulado corretamente em dias consecutivos, pode-se afirmar que esse planejamento de treino só poderá ser executado em, exatamente,
a) 12 dias
b) 13 dias
c) 14 dias
d) 15 dias
e) 16 dias
Questão 02
(ENEM, 2010) Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade de canudos (C) de cada figura depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir.

Qual expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
a) C = 4Q
b) C = 3Q + 1
c) C = 4Q – 1
d) C = Q + 3
e) C = 4Q – 2
Questão 03
(UNICAMP) No centro de um mosaico formado apenas por pequenos ladrilhos, um artista colocou 4 ladrilhos cinza. Em torno dos ladrilhos centrais, o artista colocou uma camada de ladrilhos brancos, seguida por uma camada de ladrilhos cinza, e assim sucessivamente, alternando camadas de ladrilhos brancos e cinza, como ilustra a figura a seguir, que mostra apenas a parte central do mosaico. Observando a figura, pode-se concluir que a 10ª camada de ladrilhos cinza contém:
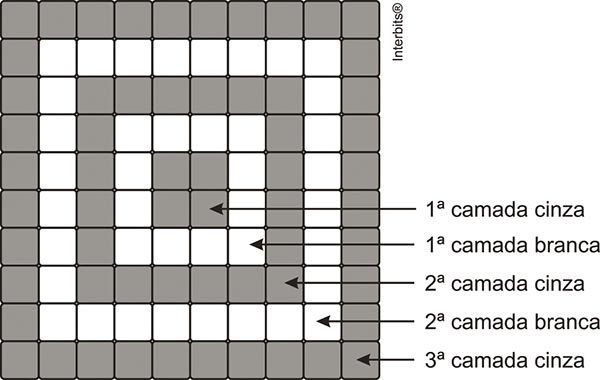
a) 76 ladrilhos
b) 156 ladrilhos
c) 112 ladrilhos
d) 148 ladrilhos
Questão 04
ENEM, 2ª aplicação, 2010) O trabalho em empresas exige dos profissionais conhecimentos de diferentes áreas. Na semana passada, todos os funcionários de uma dessas empresas estavam envolvidos na tarefa de determinar a quantidade de estrelas que seriam utilizadas na confecção de um painel de Natal.
Um dos funcionários apresentou um esboço das primeiras cinco linhas do painel, que terá, no total, 150 linhas.

Após avaliar o esboço, cada um dos funcionários esboçou sua resposta:
Funcionário I: aproximadamente 200 estrelas.
Funcionário II: aproximadamente 6 000 estrelas.
Funcionário III: aproximadamente 12 000 estrelas.
Funcionário IV: aproximadamente 22 500 estrelas.
Funcionário V: aproximadamente 22 800 estrelas.
Qual funcionário apresentou um resultado mais próximo da quantidade de estrelas necessária?
a) I
b) II
c) III
d) IV
e) V
Questão 05
(UFPB) Um produtor rural teve problema em sua lavoura devido à ação de uma praga. Para tentar resolver esse problema, consultou um engenheiro agrônomo e foi orientado a pulverizar, uma vez ao dia, um novo tipo de pesticida, de acordo com as seguintes recomendações:
• No primeiro dia, utilizar 3 litros desse pesticida.
• A partir do segundo dia, acrescentar 2 litros à dosagem anterior e, assim, sucessivamente.
Sabendo-se que nesse processo foram utilizados 483 litros de pesticida, conclui-se que esse produto foi aplicado durante:
a) 18 dias
b) 19 dias
c) 20 dias
d) 21 dias
e) 22 dias
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!