A Regra de Três; Razão e Proporção: resumo com Simulado

Exemplos de Regra de Três:

Exemplo 01 – Uma máquina varredeira limpa uma área de 5.100 m2 em 3 horas de trabalho.  Esta é a descrição da situação. Agora, vamos à pergunta que temos de resolver: Nas mesmas condições, em quanto tempo limpará uma área de 11.900 m2?

Vamos ao raciocínio para a a resolução: Há aqui duas grandezas: a área e o tempo.  Dobrando a área também se dobra o tempo; triplicando a área também se triplica o tempo, e assim por diante.

Desse modo, são grandezas diretamente proporcionais e, assim, têm o quociente constante. Veja abaixo como representar com flechas as grandezas para facilitar o raciocínio de Razão e Proporção.

Aula Gratuita de Regra de Três

Veja com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, um resumo completo sobre Regra de Três para você mandar bem nas provas e dominar razão e proporção.

Muito boa esta aula com o professor Sarkis. Ele ensina, e você aprende. Agora, veja outro exemplos de Regra de Três, com exercício resolvido:

Grandezas Diretamente Proporcionais

Apenas como recurso didático, utilizam-se duas flechas de mesmo sentido para identificar que as grandezas são diretamente proporcionais. É um fundamento para você praticar bem Razão e Proporção.

No exemplo deste exercício temos duas grandezas ( área e tempo) que são diretamente proporcionais. Veja como utilizar as flechas: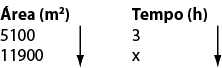Assim, com esta representação que utiliza as flexas para ‘montar o problema’, fica mais fácil também para trabalhar o cérebro e seguir adiante.

Veja o próximo passo, e a solução do problema: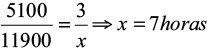

A solução clássica você já sabe: Você faz a multiplicação cruzada, montando (x . 5100) = (3 . 11900).  Em seguida você verfica que 5100.x = 35700  e, ao isolar o x , você fica com 35700 dividido por 5100 para chegar ao resultado final: x é igual a 7 horas.

Exemplo 02 de Razão e Proporção

• Um muro foi construído por 8 operários em 30 dias.
• Quantos dias seriam necessários para a construção deste mesmo muro, se fossem utilizados 12 operários?

Acompanhe a Resolução: Novamente estamos diante de duas grandezas: operários e dias. Mas, aqui, ao tempo em que uma aumenta (operários) a outra diminui (dias). Pensando em Razão e Proporção, você poderia escrever que elas têm uma relação inversa neste caso: são grandezas inversamente proporcionais, e por isso as setas invertidas.

Veja: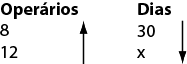Uma maneira de resolver é utilizando o conceito de grandezas, que são inversamente proporcionais: produto constante.

Pode ser assim: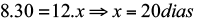

Dica de resolução > Outra forma é usar o recurso didático das flechas, como indicado acima. Se são inversamente proporcionais, as flechas são colocadas em sentido contrário.

A seguir criou-se uma proporção, mantendo-se a fração onde se encontra a incógnita e invertendo-se a outra.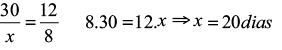

2 – Regra de Três Composta

Agora vamos mudar de patamar um pouco, e aprender (ou revisar) Regra de Três Composta. Uma regra de três é considerada composta quando envolver três ou mais grandezas para que se estabeleçam entre elas a Razão e a Proporção.

Exemplos para você  não esquecer Razão e Proporção

Exemplo 01 – Uma casa é construída por 40 operários trabalhando 9 horas por dia durante 6 dias. Em quantos dias 24 operários poderiam construir a mesma casa, trabalhando 5 horas por dia?

Resolução: Perceba que ao contrário do exemplo 01 agora nós temos 3 (tres) grandezas para trabalhar: operários, as horas trabalhadas por dia, e os dias (duração da obra):

Inicia-se colocando uma flecha para baixo na grandeza que possui a incógnita (dias) e a seguir compara-se com as outras duas. Operários e dias são grandezas inversamente proporcionais e horas por dia e dias também são inversamente proporcionais.

Portanto, as flechas nessas grandezas devem ter sentido contrário:

Para finalizar esse dispositivo prático, iguala-se a fração que contém a incógnita ao produto das demais, respeitando o sentido das flechas.

Veja como “armar a conta” bem certinho, observando o sentido das flechas: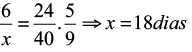

Veja aula gratuita com exercício resolvido de Regra de Três

Confira também um resumo do Curso Enem Gratuito, com mais exemplos de resolução de problemas de Regra de Três.

Gostou da aula? No final do post tem um desafio do Simulado de Regra de Três & Razão e Proporção.

Veja outros temas que sempre caem no Enem e no Encceja:

1. Geometria Plana – Triângulos, Círculos e Quadriláteros
2. Probabilidade
3. Funções de 1º Grau e de 2º Grau
4. Trigonometria

Como estudar Matemática Básica

Uma ótima maneira de estudar Matemática é através da resolução de exercícios. Você pode  é resolvendo os nossos Simulados Encceja & Enem. Cada um tem no máximo 10 questões e, se você errar alguma resposta, já terá a indicação de qual aula estudar para aprender o conteúdo correspondente.

Outra dica é fazer o download das provas anteriores do Encceja, o download das provas do Enem, imprimir e resolvê-las. Com esse treino, você vai se acostumar ao tipo de enunciado usado pelo Encceja e ao estilo da prova, para não ter nenhuma surpresa quando chegar o dia da prova oficial! Veja o que estudar de Matemática para o Encceja:

3 – Geometria Plana

Este é outro conteúdo da Matemática que pode ser facilmente contextualizado em diversas situações do nosso dia-a-dia. Por este motivo, a geometria plana é um tema com grandes chances de ser cobrado nas provas do Encceja & do Enem.

A geometria plana abarca o estudo das figuras geométricas bidimensionais, como triângulos, círculos e quadrados. As questões costumam cobrar o cálculo de área, perímetro e altura, além de propriedades das figuras planas.

Assista à aula abaixo para ver como a geometria plana pode ser cobrada nas provas:

Interessante, não? Vamos ao próximo!

4 – Probabilidade

A probabilidade é mais um tema presente em nosso cotidiano que pode facilmente ser contextualizada no enunciado de uma questão do Encceja ou do Enem. Por exemplo, problemas que envolvam jogos com dados e cartas, ou sorteios, podem ser resolvidos com os conhecimentos sobre probabilidade.

Este é um tema da Matemática que pode ser bastante complexo, mas algumas questões podem ser resolvidas com raciocínio lógico e operações simples.

Veja um exemplo de questão sobre probabilidade que já caiu no Encceja e como resolvê-la:

Conseguiu resolver a questão junto com o professor? Tente imaginar outras possibilidades de contextualização de um problema envolvendo a probabilidade!

5 – Funções Matemáticas

As funções matemáticas podem ser de primeiro ou segundo grau. No Encceja, o mais comum é a cobrança da resolução de uma função de primeiro grau, mas você deve estar preparado para resolver funções de segundo grau também, através da famosa fórmula de bháskara!

Assista na aula abaixo um exemplo de questão envolvendo funções matemáticas que já caiu no Encceja e acompanhe sua resolução. No Enem também sempre cai:

Viu como não precisa ser complicado?

6 – Trigonometria

A trigonometria trata das relações métricas nos triângulos. Como sempre, as questões de trigonometria do Encceja virão contextualizadas – normalmente o enunciado trazer o desenho do posicionamento de objetos que, entre si, formam um triângulo, ou então vai descrever essa situação.

Ou seja, o enunciado não vai dizer de cara que essa é uma questão de trigonometria, mas você deve estar preparado para identificar o conhecimento exigido pela prova!

Veja como isso pode acontecer na sua prova do Enem ou do Encceja:

Recapitulando

O nível de dificuldade da prova do Encceja não pode ser desprezado: é importante estudar para chegar bem preparado à prova!

No estudo da Matemática, o melhor jeito de se preparar é resolvendo exercícios. Aqui no Blog do Enem, você pode fazer isso resolvendo os nossos Simulados do Encceja ou baixando as provas anteriores. Pratique muito para conseguir responder às questões o mais rápido possível e para não ter surpresas no dia do Encceja!

Por último, lembre-se de também estudar as outras áreas de conhecimento cobradas pela prova e, principalmente, treinar a Redação do Enem ou do Encceja! Assim como a Matemática, ela exige uma preparação prévia do candidato, então dedique um tempinho ao treino da redação também!

7 – Simulado Enem Gratuito de Regra de Três

Resolva abaixo os 10 exercícios para se qualificar para a Matemática do Enem. O Gabarito sai na hora, e você tem aulas de reforço quando não acerta a questão.

Mais Exercícios sobre Regra de Três, Razão e Proporção

Exercício 01

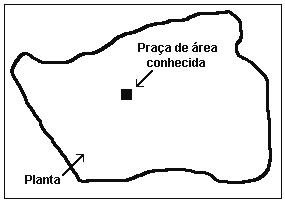
(ENEM, 2001) Um engenheiro, para calcular a área de uma cidade, copiou sua planta numa folha de papel de boa qualidade, recortou e pesou numa balança de precisão, obtendo 40 g. Em seguida, recortou, do mesmo desenho, uma praça de dimensões reais 100 m × 100 m, pesou o recorte na mesma balança e obteve 0,08 g. Com esses dados foi possível dizer que a área da cidade, em metros quadrados, é de, aproximadamente,

a) 800

b) 10.000

c) 320.000

d) 400.000

e) 5.000.000

Dica 1 – Você já sabe tudo sobre polinômios? Nesta aula de Matemática Enem vamos aprender Adição, Subtração, Multiplicação e Divisão polinomial – https://blogdoenem.com.br/definicoes-propriedades-dos-polinomios-matematica-enem/

Exercício 02

(ENEM, 2010) Um dos grandes problemas da poluição dos mananciais (rios, córregos e outros) ocorre pelo hábito de jogar óleo utilizado em frituras nos encanamentos que estão interligados com o sistema de esgoto. Se isso ocorrer, cada 10 litros de óleo poderão contaminar 10 milhões (107) de litros de água potável.

Suponha que todas as famílias de uma cidade descartem o óleo das frituras nos encanamentos e consumam 1.000 litros de óleo em frituras por semana. Qual seria, em litros, a quantidade de água potável contaminada por semana nessa cidade?

a) 102

b) 103

c) 104

d) 105

e) 109

Dica 2 – Que tal revisar Funções Polinomiais? Confira exercícios resolvidos nesta aula de Matemática Enem para lhe ajudar a fixar o conteúdo – https://blogdoenem.com.br/funcoes-polinomiais-matematica-enem/

Exercício 03

(FCC-SP,) Se 25 operários trabalhando 10 horas por dia abriram um canal com 238 m de comprimento em 17 dias, quantos operários serão necessários para abrir 686 m do mesmo canal em 25 dias de 7 horas de trabalho?

Exercício 04

(UNIMEP) Se dois gatos comem dois ratos em dois minutos, para comer 60 ratos em 30 minutos serão necessários:

a) 4 gatos

b) 3 gatos

c) 2 gatos

d) 5 gatos

e) 6 gatos

Dica 3 – Estude para o Exame Nacional do Ensino Médio com esta aula de Funções Polinomiais de 2º grau para a prova de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-2o-grau-matematica-enem/

Exercício 05

(UFMG) No ano passado, uma equipe de 13 professores, com um ritmo de trabalho supostamente constante, corrigiu 3.000 provas em 6 dias. Este ano, o número de provas aumentou para 5.500 e a equipe foi ampliada para 15 professores. Para se obter uma estimativa do número n de dias necessários para totalizar a correção, suponha que, durante todo o período de correção, o ritmo de trabalho da equipe deste ano será o mesmo da equipe do ano passado. O número n satisfaz a condição:

a) n ≤ 8

b) 8 < n ≤ 10

c) 10 < n ≤ 12

d) n > 12

Questão 06

(ENEM cancelado, 2009) Os calendários usados pelos diferentes povos da Terra são muito variados. O calendário islâmico, por exemplo, é lunar, e nele cada mês tem sincronia com a fase da Lua. O calendário maia segue o ciclo de Vênus, com cerca de 584 dias, e cada 5 ciclos de Vênus corresponde a 8 anos de 365 dias da Terra.

Quantos ciclos teria, em Vênus, um período terrestre de 48 anos?

a) 30 ciclos

b) 40 ciclos

c) 73 ciclos

d) 240 ciclos

e) 384 ciclos

Questão 07

(ENEM cancelado, 2009) Pneus usados geralmente são descartados de forma inadequada, favorecendo a proliferação de insetos e roedores e provocando sérios problemas de saúde pública. Estima-se que, no Brasil, a cada ano, sejam descartados 20 milhões de pneus usados. Como alternativa para dar uma destinação final a esses pneus, a Petrobras, em sua unidade de São Mateus do Sul, no Paraná, desenvolveu um processo de obtenção de combustível a partir da mistura dos pneus com xisto. Esse procedimento permite, a partir de uma tonelada de pneu, um rendimento de cerca de 530 kg de óleo.

Considerando que uma tonelada corresponde, em média, a cerca de 200 pneus, se todos os pneus descartados anualmente fossem utilizados no processo de obtenção de combustível pela mistura com xisto, seriam então produzidas:

a) 5,3 mil toneladas de óleo.

b) 53 mil toneladas de óleo.

c) 530 mil toneladas de óleo.

d) 5,3 milhões de toneladas de óleo.

e) 530 milhões de toneladas de óleo.

Questão 08

(ENEM, 2009) Uma escola lançou uma campanha para seus alunos arrecadarem, durante 30 dias, alimentos não perecíveis para doar a uma comunidade carente da região. Vinte alunos aceitaram a tarefa e nos primeiros 10 dias trabalharam 3 horas diárias, arrecadando 12 kg de alimentos por dia. Animados com os resultados, 30 novos alunos somaram-se ao grupo, e passaram a trabalhar 4 horas por dia nos dias seguintes até o término da campanha.

Admitindo-se que o ritmo de coleta tenha se mantido constante, a quantidade de alimentos arrecadados ao final do prazo estipulado seria de:

a) 920 kg

b) 800 kg

c) 720 kg

d) 600 kg

e) 570 kg

Questão 09

(ENEM, 2011) Muitas medidas podem ser tomadas em nossas casas visando à utilização racional de energia elétrica. Isso deve ser uma atitude diária de cidadania. Uma delas pode ser a redução do tempo no banho. Um chuveiro com potência de 4.800 kWh consome 4,8 kW por hora.

Uma pessoa que toma dois banhos diariamente, de 10 minutos cada, consumirá, em sete dias, quantos kW?

a) 0,8

b) 1,6

c) 5,6

d) 11,2

e) 33,6

Questão 10

(PUCAMP) Sabe-se que 5 máquinas, todas de igual eficiência, são capazes de produzir 500 peças em 5 dias, se operarem 5 horas por dia. Se 10 máquinas iguais as primeiras operassem 10 horas por dia durante 10 dias, o número de peças produzidas seria:

a) 1.000

b) 2.000

c) 4.000

d) 5.000

e) 8.000

 Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!