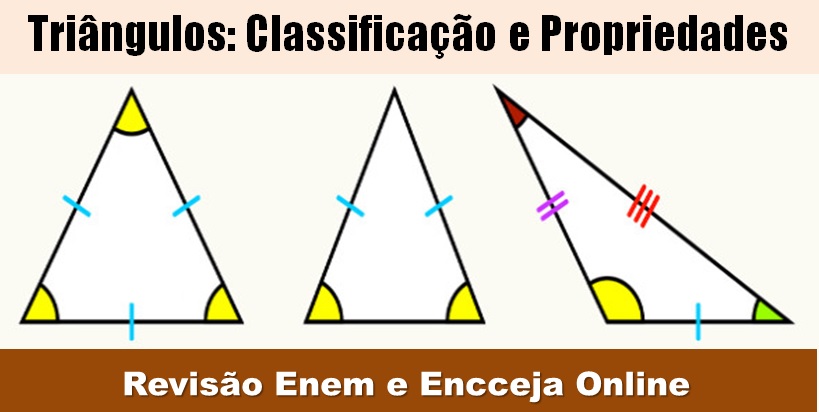
Você lembra tudo sobre as definições e propriedades dos triângulos Reto, Equilátero, Escaleno, Agudo, Equiângulo e Isósceles? Vem, que o Blog do Enem te ajuda com um super resumo de trigonometria. Bora lá gabaritar em Triângulos na prova!
Triângulos são figuras planas, formadas por três segmentos de retas delimitando uma região fechada. Isso você lembra ‘de primeira’, certo? Mas e as Propriedades do Triângulo? – Vamos revisar, pois cai no Enem e no Vestibular.
Perceba na imagem abaixo como o Triângulo está presente em cada uma das faces da Pirâmide. Como ela tem três lados, a base dela no chão também forma um triângulos. Pois então, quando você avista um dos lados da pirâmide, você está olhando um triângulo.
Vamos estudar quais são os elementos geométricos que compõe os triângulos? E as propriedades pertinentes a esses elementos? Se liga! Esse conteúdo é bastante cobrado em provas do Enem e dos vestibulares.
Os Elementos do Triângulo:
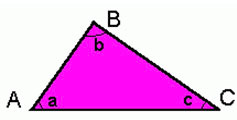
1) Vértices: são os pontos A, B e C, o vértice de um triângulo é o encontro de dois lados dessa figura, assim como uma esquina, é o encontro de duas ruas.
2) Ângulos internos: a, b e c, são os ângulos formados no encontro de dois lados do triângulo, ou seja, o vértice.
3) Lados: AB, AC e BC, é cada linha que forma o triângulo.
4) Altura: é um segmento de reta traçado a partir de um vértice de forma a encontrar o lado oposto ao vértice formando um ângulo reto (90º). BH é uma altura do triângulo.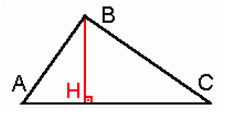
5) Ângulo externo: é formado por um dos lados do triângulo e pelo prolongamento do lado adjacente.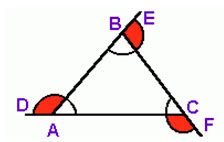 Na figura acima são ângulos externos os ângulos D, E, F.
Na figura acima são ângulos externos os ângulos D, E, F.
Introdução aos Triângulos
Confira agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, um resumo básico para você dominar o conteúdo sobre os Triângulos.
Dicas sobre os Triângulos:
- A soma dos ângulos internos de qualquer triângulo é sempre igual a 180º.
- A soma dos ângulos externos de qualquer triângulo é sempre igual a 360º.
- Cada ângulo externo é igual à soma dos outros dois internos não adjacentes a ele.
- O maior lado do triângulo está sempre oposto ao maior ângulo desse triângulo.
Isto você não pode esquecer:
O Perímetro é a soma dos lados. Perímero = AB + AC + BC
A Classificação dos Triângulos
Você sabe como são classificados os triângulos? Não se preocupe o Blog do Enem te ajuda a entender mais essa! Não deixe essa chance passar. 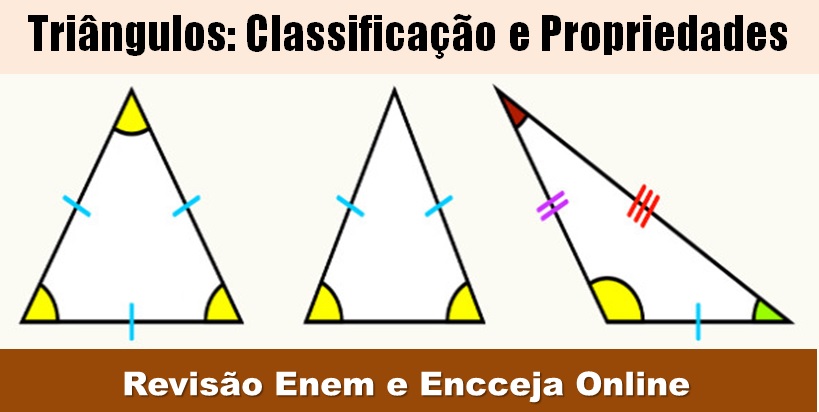 Um triângulo pode ser classificado de acordo com as medidas relativas de seus lados:
Um triângulo pode ser classificado de acordo com as medidas relativas de seus lados:
- Um triângulo equilátero possui todos os lados congruentes (iguais). Pode-se verificar que um triângulo equilátero é também equiângulo, ou seja, possui todos os seus ângulos internos congruentes (e com medida 60°). Por este motivo, este tipo de triângulo é também um polígono regular.
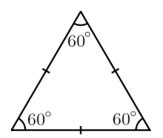 Triângulo eqüilátero
Triângulo eqüilátero
Em particular, como seus lados são dois a dois congruentes, ele é um triângulo isósceles. Pode-se observar que todos os seus ângulos internos medem 60° e por isso ele é equiângulo.
- Um triângulo isósceles possui pelo menos dois lados congruentes. Neste triângulo o ângulo formado pelos lados congruentes denomina-se ângulo do vértice. Os demais ângulos denominam-se ângulos da base e, como se pode verificar, são congruentes. Note que os triângulos equiláteros também são isósceles.
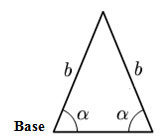 Triângulo isósceles
Triângulo isósceles
Observe que neste triângulo há somente dois lados congruentes: os que têm medida b. Por este motivo, o triângulo é isósceles, mas não é equilátero. Além disso, cada um destes dois lados forma um ângulo de medida α com a base do triângulo.
Quer ver como são cobrados os exercícios com os triângulos equiláteros e isósceles? Então assista a videoaula da Khan Academy, traduzido para o Português pela Fundação Lemann, onde o professor Salman Khan explica como se resolve esse tipo de exercício. Vamos nessa?
Você pode ver esta aula na plataforma da Khan: https://goo.gl/fqhaF6
- Em umtriângulo escalenoas medidas dos três lados são diferentes. É possível mostrar que os ângulos internos de um triângulo escaleno também possuem medidas diferentes.
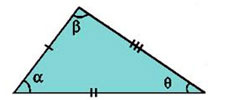 Triângulo escaleno
Triângulo escaleno
Aqui, cada um dos lados tem um comprimento diferente dos demais. Observe ainda que todos os seus ângulos internos são diferentes entre si.
Não esqueça!
1) A base de um triângulo é o lado sobre qual apoia-se o triângulo.
2) No triângulo isósceles, considera-se base o lado de medida diferente e sobre ele estarão localizados os ângulos congruentes (iguais) do triângulo.
Quer saber mais sobre figuras planas? Então acesse o Blog do Enem e revise esse conteúdo com um super- resumo que o Blog do Enem preparou para você. Não deixe de conferir! https://blogdoenem.com.br/planos-poligonos-matematica/
Classificação dos Triângulos pelos Ângulos Internos
Agora que já vimos a classificação dos triângulos quanto ao seu lado, vamos relembrar a sua classificação quanto aos seus ângulos internos?
- Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados denominam-se catetos.
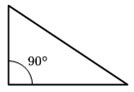
Triângulo retângulo
- Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.
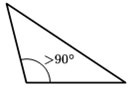
Triângulo obtusângulo
Esse triângulo possui um ângulo reto (90º), um ângulo obtuso (> 90º) e dois ângulos agudos.
- Em um triângulo acutângulo, todos os três ângulos são agudos.
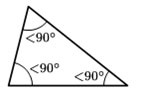
Triângulo acutângulo
Todos os três ângulos são agudos (< 90º).
O Triângulo Retângulo e o Teorema de Pitágoras
Veja agora um conteúdo clássico, que é a base da trigonometria em toda a matemática. Confira o Triângulo Retângulo e o Teorema de Pitágoras.
As dicas do professor Sarkis:
- Esse triângulo se chama retângulo porque tem um ângulo reto (90º). O lado que estiver diante do ângulo reto será a hipotenusa. E os lados que formam o ângulo reto são chamados de catetos.
- Veja no exemplo durate a aula que o professor traça uma reta que corresponde à altura relativa à hipotenusa. Confira a demonstração na lousa, na qual o prof também explica o que são projeções.
- De todas as relações métricas que existem, o Teorema de Pitágoras é o mais recorrente no Enem e nos vestibulares.
- O Teorema de Pitágoras diz que o quadrado da hipotenusa deve ser igual à soma do quadrado dos catetos: hip² = cat² + cat².
- Veja agora no resumo acima.
Conseguiu relembrar tudo sobre triângulos? Você consegue resolver este exercício? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
Um triângulo isósceles tem um dos ângulos internos iguais a 100°. Qual é o valor do menor ângulo deste triângulo?
- a) 20º
- b) 30º
- c) 40º
- d) 45º
- e) 50º
Resposta: c