Preparado para as questões mais avançadas de Matemática no Vestibular e no Enem? Revise sobre Trigonometria para se garantir. Quem acerta uma questão deste conteúdo já sai na frente. Veja a revisão gratuita abaixo.
A trigonometria é um campo da matemática que ainda põe medo em muitos alunos. Quando falamos em seno, cosseno e tangente, tem quem até se arrepie! Todavia, a matéria é mais simples do que parece e ainda por cima é figurinha carimbada no Enem e nos vestibulares. Aqui, vamos simplificar o círculo trigonométrico para você!
Para compreender e desvendar os segredos da trigonometria, o primeiro passo é entender o ciclo trigonométrico. Observe a imagem, e tente recuperar os conteúdos relacionados que você já estudou antes de prosseguir na leitura. É um bom exercício para você refrescar a memória, lembrar o que sabe, e recuperar as dúvidas também.
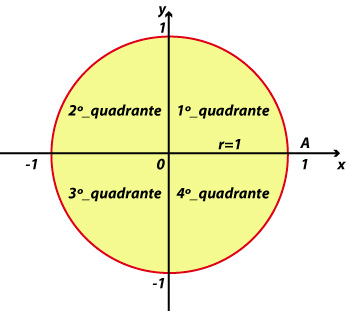
Então quando formamos qualquer ângulo a partir da origem, surgem dois vetores, um no eixo das abscissas, e outro no das ordenadas, assim formando no eixo X os cossenos, e no eixo Y o seno, os quais possuem um valor entre 0 e 1, e a tangente é um valor formado prolongando o vetor do ângulo até uma reta tangente à circunferência, assim formando um terceiro vetor chamado de tangente, de varia de 0 até tendendo a +/- infinito. 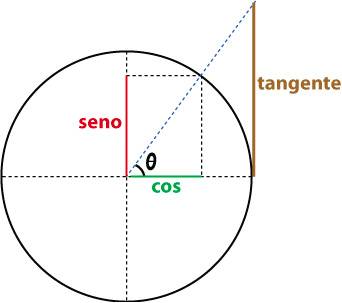
Seno e Cosseno:
Os sinais de seno, cosseno e tangente são respectivamente:
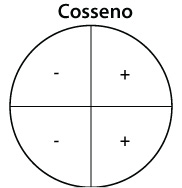
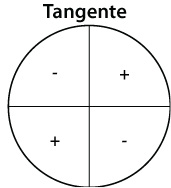
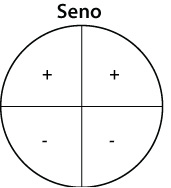
Veja as Relações do Círculo Trigonométrico
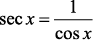
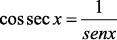
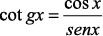
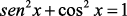
Exercício Resolvido de Trigonometria
O valor de y = cos 150° + sen 300° – tg 225° – cos 90° é
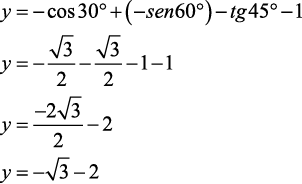
Sendo sen x = – 4/5 e 3π/2 < x < 2π, então a tg x é igual a
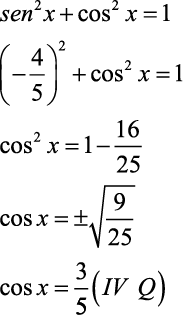
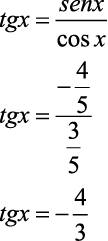
Que tal revisar seus conhecimentos com o Curso Enem Gratuito? Veja o vídeo abaixo e revise com a gente!
É hora de descobrir se você entendeu. Resolva os desafios abaixos:
Questão 1
(G1 – cftmg 2007) Sabendo-se que
cos a = 3/5 e 0 < a < π/2, pode-se afirmar que tg a vale
a) 4/3
b) 1
c) 5/6
d) 3/4
Questão 2
(G1 – cftmg 2005) O número
N = (3 cos180° – 4 sen210° + 2 tg135°) / (6 sen245°)
pertence ao intervalo
a) ] -4 , -3 [
b) [ -3 , -2 [
c) [ -2 , -1 ]
d) ] -1 , 0 ]
Dica 2 – Confira a aula sobre Logaritmos que preparamos para você gabaritar na prova de Matemática Enem – https://blogdoenem.com.br/logaritmos-revisao-matematica-enem/
Questão 3
(Unesp 2003) Um farol localizado a 36 m acima do nível do mar é avistado por um barco a uma distância x da base do farol, a partir de um ângulo á, conforme a figura:
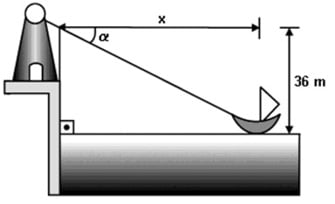
a) Admitindo-se que sen(a) =  , calcule a distância x.
, calcule a distância x.
b) Assumindo-se que o barco se aproximou do farol e que uma nova observação foi realizada, na qual o ângulo á passou exatamente para 2a, calcule a nova distância x’ a que o barco se encontrará da base do farol.
Questão 4
(Fatec 2000) Se x é um arco do 30. quadrante e cosx = -4/5, então cossecx é igual a
a) -5/3
b) -3/5
c) 3/5
d) 4/5
e) 5/3
Questão 5
(Fatec 1995) O conjunto solução da equação 2cos2x + cosx – 1 = 0, no universo U = [0, 2π], é
a) {π/3, π, 5π/3}
b) {π/6, π, 5π/6}
c) {π/3, π/6, π}
d) {π/6, π/3, π, 2π/3, 5π/3}
e) {π/3, 2π/3, π, 4π/3, 5π/3, 2π}



