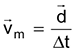Cai sempre no Enem e no vestibular o cálculo em Física com o uso de Vetores. Em um dado movimento, os vetores representam direção e sentido, e daí surge uma resultante. Você lembra? Entenda como correlacionar essas grandezas nesta aula de Física Enem. Veja abaixo, com exercícios.
Você lembra das aulas sobre como fazer a Soma Vetorial? Tem na ponta da língua a diferença entre sentido e direção? Você sabe fazer a soma vetorial? Veja aqui uma revisão gratuita para o Enem e o Vestibular. O que e um Vetor?
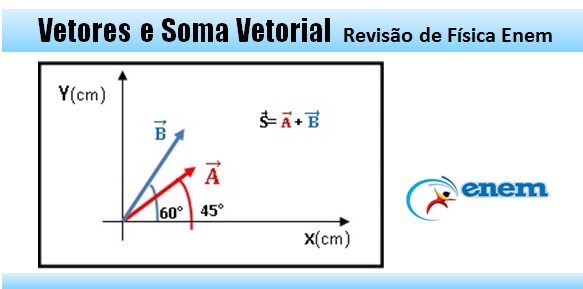
Vetor é um segmento de reta que possui como características fundamentais módulo direção e sentido. Tal representação será utilizada porque estaremos interessados em estudar grandezas envolvidas em nosso cotidiano que precisam de mais do que um valor numérico para serem bem interpretadas.
A Soma de Vetorial
Tais grandezas serão assim chamadas vetoriais, assim, antes de contextualizarmos tais grandezas, precisamos de um estudo formal de vetores.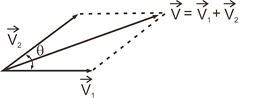
Veja na representação gráfica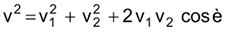 
Resumo de Soma Vetorial
Acompanhe agora com o professor Rossetto, do canal do Curso Enem Gratuito, como resolver a Soma Vetorial com o método do Paralelogramo:
Subtração de Vetores – Revise!
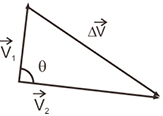Agora, na representação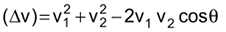 
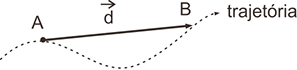
O Deslocamento
Velocidade Vetorial Média
Velocidade Vetorial Instantânea
a. Módulo:
b. Direção: tangente à trajetória
c. Sentido: o mesmo do movimento
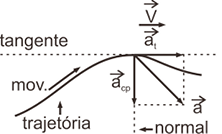
Aceleração Vetorial Instantânea
a. Componentes
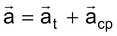
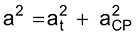
Dica 1 – Física Enem – Revise sobre Gráficos e Movimentos Notáveis – https://blogdoenem.com.br/graficos-movimentos-notaveis-fisica-enem/
Dica 2 – Física Enem – Relembre os fundamentos da Cinemática – https://blogdoenem.com.br/fisica-enem-cinematica/
Dica 3 – Física no Enem – Notação Científica – Veja como cai no Enem – https://blogdoenem.com.br/fisica-enem-notacao-cientifica/
Veja nossa aula sobre grandezas físicas e estude para o Enem!
Exercicios – Desafios de Soma Vetorial
Questão 1
(Pucrj) Um pequeno avião acelera, logo após a sua decolagem, em linha reta, formando um ângulo de 45o com o plano horizontal. Sabendo que a componente horizontal de sua aceleração é de 6,0 m/s2, calcule a componente vertical da mesma.
(Considere g = 10 m/s2)
a) 6,0 m/s2
b) 4,0 m/s2
c) 16,0 m/s2
d) 12,0 m/s2
e) 3,0 m/s2
Questão 2 – Soma Vetorial
(Uece) Um corpo move-se no plano XY, sendo as coordenadas de sua posição dadas pelas funções e, em centímetros, com t em segundos. O módulo do deslocamento entre os instantes t = 0 e t = 4 segundos, em centímetros, é
a) 4.
b) 20.
c) 38.
d) 48.
Questão 3
(Puc-rio) Um veleiro deixa o porto navegando 70 km em direção leste. Em seguida, para atingir seu destino, navega mais 100 km na direção nordeste. Desprezando a curvatura da terra admitindo que todos os deslocamentos são coplanares, determine o deslocamento total do veleiro em relação ao porto de origem.
(Considere = 1,40 e = 2,20)
a) 106 km
b) 34 km
c) 154 km
d) 284 km
e) 217 km
Questão 4
(Ufpb) Considere os vetores A, B e F, nos diagramas numerados de I a IV.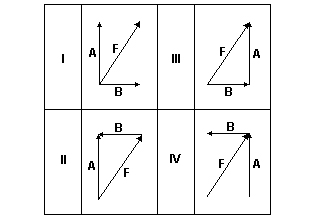
Os diagramas que, corretamente, representam a relação vetorial F = A – B são apenas:
a) I e III
b) II e IV
c) II e III
d) III e IV
e) I e IV
Questão 5
(Puc-rio) Os ponteiros de hora e minuto de um relógio suíço têm, respectivamente, 1 cm e 2 cm. Supondo que cada ponteiro do relógio é um vetor que sai do centro do relógio e aponta na direção dos números na extremidade do relógio, determine o vetor resultante da soma dos dois vetores correspondentes aos ponteiros de hora e minuto quando o relógio marca 6 horas.
a) O vetor tem módulo 1 cm e aponta na direção do número 12 do relógio.
b) O vetor tem módulo 2 cm e aponta na direção do número 12 do relógio.
c) O vetor tem módulo 1 cm e aponta na direção do número 6 do relógio.
d) O vetor tem módulo 2 cm e aponta na direção do número 6 do relógio.
e) O vetor tem módulo 1,5 cm e aponta na direção do número 6 do relógio.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
