Critérios de Divisibilidade em N – Matemática Enem

Hora de ganhar tempo para resolver questões de prova. Dominar os Critérios de Divisibilidade acelera na resolução da Matemática. Veja os macetes de divisibilidade por 2, 3, 4 e até por 11

• Vamos começar pelo começo… Veja os critérios de Divisibilidade por 2:
• Um número é divisível por 2 quando é par.
• Exemplos: 48, 2854, 35986, etc.
• Viu como é simples?

 

Veja os critérios de divisibilidade agora para os números 3, 4, 5 6, 7, 8, 9, 10 e o 11. É rápido para aprender, e você ganha no raciocínio na hora das provas.

Divisibilidade por 3:

• Um número é divisível por 3 quando a soma de seus algarismos for divisível por 3. 
• Exemplos:
• 1) 12981 é divisível por 3, pois 1+2+9+8+1 = 21 é divisível por 3.
• 2) 3403 não é divisível por 3, porque 3+4+0+3 =10 não é divisível por 3

 

Critérios de Divisibilidade por 4:

• Um número é divisível por 4 se o número formado pelos seus dois últimos algarismos é divisível por 4.
• Exemplos:
• 1) 5508728 é divisível por 4, pois 28 é divisível por 4;
• 2) 2200 é divisível por 4, pois 00 é divisível por 4;
• 3) 237550 não é divisível por 4, porque 50 não é divisível por 4.

 

• Divisibilidade por 5:
• Um número é divisível por 5 quando o seu algarismo das unidades é 0 ou 5.
• Exemplos: 3120, 1275, 65, etc.

 

Divisibilidade por 6:

• Um número é divisível por 6 quando for simultaneamente divisível por 2 e por 3, isto é, quando for par e tiver a soma dos seus algarismos divisível por 3.
• Exemplos:
• 1) 3483 não é divisível por 6, porque não é par;
• 2) 9824 não é divisível por 6, porque 9+8+2+4 = 23 não é divisível por 3.
• 3) 624 é divisível por 6, porque além de ser par, tem a soma dos seus algarismos divisível por 3.

 

Divisibilidade por 7: Um número x é divisível por 7 se a subtração entre o número que se obtém de x suprimindo o seu algarismo das unidades e o dobro desse algarismo (unidade) for divisível por 7.

• Exemplos:
• 1) 385 é divisível por 7, pois 38 – 2.5 = 28 é divisível por 7;
• 2) 93 não é divisível por 7, pois 9 – 2.3 = 3 não é divisível por 7.
• 3) Vamos considerar agora um número maior, de 5 dígitos, por exemplo, 43.234.

Em princípio faremos a diferença 4323 – 2.4 = 4315. Para verificar se esse número é divisível por 7 devemos aplicar novamente o critério de divisibilidade, ou seja, 431 – 2.5 = 421. Novamente aplicando o critério, 42 – 2.1 = 40 que não é divisível por 7. Assim, o número inicial também não é divisível por 7.

Critérios de Divisibilidade por 8:

Um número é divisível por 8 se o número formado pelos seus três últimos algarismos é divisível por 8.

• Exemplos:
• a) 54872 é divisível por 8, porque 872 é divisível por 8.
• b) 1844 não é divisível por 8, pois 844 não é divisível por 8.
• c) 10188 não é divisível por 8, porque 188 não é divisível por 8.

 

Divisibilidade por 9:

• Um número é divisível por 9 quando a soma de seus algarismos for divisível por 9.
• Exemplos:
• 1) 12981 não é divisível por 9, pois 1+2+9+8+1 = 21 não é divisível por 9.
• 2) 52821 é divisível por 8, porque 5+2+8+2+1 = 18 é divisível por 9

 

Divisibilidade por 10: Um número é divisível por 10 quando o seu algarismo das unidades é 0.

Exemplos: 100, 640, 1870 são divisíveis por 10

 

Divisibilidade por 11:

• Basta atribuir aos algarismos do número considerado sinais de + e de -, alternadamente, da esquerda para direita (ou direita para a esquerda) e efetuar essa soma algébrica. Se o resultado obtido for divisível por 11, então o número inicial também será divisível por 11.
• Exemplos:
• 1) 192918 é divisível por 11, pois 1-9+2-9+1-8 = -22, que é divisível por 11.
• 2) 3192 não é divisível por 11, porque 3-1+9-2 =9 não é divisível por 11.

Continue estudando sobre critérios de divisibilidade com a videoaula do prof. Lucas:

Gostou do resumo do professor Lucas? Têm mais aulas com ele no canal do Curso Enem Gratuito!

Exercício Resolvido sobre  Critérios de Divisibilidade

Qual o maior valor do algarismo a a fim de que o número 27a5 seja divisível por 3?

Gabarito: 7

Operações com Frações: Adição e Subtração

Denominadores iguais – basta manter os denominadores e somar os numeradores. Exemplos:

1)

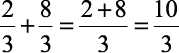
2)

 

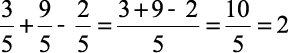
Outro Exemplo:

Denominadores diferentes – inicialmente devemos tirar o m.m.c. dos denominadores. Em seguida dividimos esse denominador pelo antigo e multiplicamos o resultado pelo numerador, a fim de obtermos frações com denominadores iguais.

Exemplos:

1) 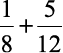O m.m.c. entre 8 e 12 é 24.

Assim,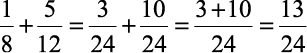

2)

 

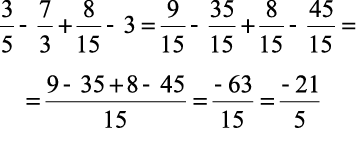
Operações com Frações: Multiplicação

Neste caso basta multiplicar numerador com numerador e denominador com denominador.

Exemplo:

1)

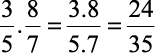
2)

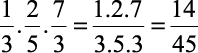
Operações com Frações: Divisão

Mantemos a primeira fração e invertemos a segunda, invertendo também a operação para multiplicação.

Exemplos:

1)

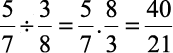
2)

 

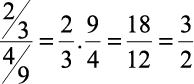
Operações com Frações: Número Misto

É comum encontrarmos em livros de receita expressões do tipo “1½ xícara de leite” ou “3½ copos de água”, etc. Esses são exemplos de números mistos. Na verdade é apenas uma representação diferente para a soma de um número inteiro com uma fração.

Exemplos:

1) 1½ =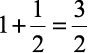

2) 3½ =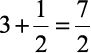

3) 73/4 =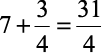

Dica 1 – Matemática Enem – revise os Múltiplos e Divisores! 

Desafios sobre os Critérios de Divisibilidade

Questão 1

O maior valor do algarismo a a fim de que o número 385a seja divisível por 3 é:

a) 2 b) 3 c) 5 d) 7 e) 8

Questão 2

(Enem 2008)

Para contar os 1.268 bois de acordo com o processo descrito no texto, o marcador utilizou

a) 20 vezes todos os dedos da mão esquerda.

b) 20 vezes todos os dedos da mão direita.

c) todos os dedos da mão direita apenas uma vez.

d) todos os dedos da mão esquerda apenas uma vez.

e) 5 vezes todos os dedos da mão esquerda e 5 vezes todos os dedos da mão direita.

Dica 2 – Matemática Enem – Revise tudo sobre os números Naturais! 

Questão 3

(Enem 2010) A disparidade de volume entre os planetas é tão grande que seria possível colocá-los uns dentro dos outros. O planeta Mercúrio é o menor de todos. Marte é o segundo menor: dentro dele cabem três Mercúrios. Terra é o único com vida: dentro dela cabem sete Martes. Netuno e o quarto maior: dentro dele cabem 58 Terras. Júpiter é o maior dos planetas: dentro dele cabem 23 Netunos. Revista Veja. Ano 41, nº. 26, 25 jun. 2008 (adaptado)

Seguindo o raciocínio proposto, quantas Terras cabem dentro de Júpiter?

a) 406 b) 1 334 c) 4 002 d) 9 338 e) 28 014

Questão 4

(Enem 2009) Nos últimos anos, o volume de petróleo exportado pelo Brasil tem mostrado expressiva tendência de crescimento, ultrapassando as importações em 2008.

Entretanto, apesar de as importações terem se mantido praticamente no mesmo patamar desde 2001, os recursos gerados com as exportações ainda são inferiores àqueles despendidos com as importações, uma vez que o preço médio por metro cúbico do petróleo importado é superior ao do petróleo nacional. Nos primeiros cinco meses de 2009, foram gastos 2,84 bilhões de dólares com importações e gerada uma receita de 2,24 bilhões de dólares com as exportações. O preço médio por metro cúbico em maio de 2009 foi de 340 dólares para o petróleo importado e de 230 dólares para o petróleo exportado.

O quadro a seguir mostra os dados consolidados de 2001 a 2008 e dos primeiros cinco meses de 2009.

Comércio exterior de petróleo
(milhões de metros cúbicos)

Ano	Importação	Exportação
2001	24,19	6,43
2002	22,06	13,63
2003	19,96	14,03
2004	26,91	13,39
2005	21,97	15,93
2006	20,91	21,36
2007	25,38	24,45
2008	23,53	25,14
2009*	9,00	11,00

*Valores apurados de janeiro a maio de 2009.

Disponível em: http://www.anp.gov.br. Acesso em: 15 jul. 2009 (adaptado).

Considere que as importações e exportações de petróleo de junho a dezembro de 2009 sejam iguais a 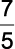das importações e exportações, respectivamente, ocorridas de janeiro a maio de 2009. Nesse caso, supondo que os preços para importação e exportação não sofram alterações, qual seria o valor mais aproximado da diferença entre os recursos despendidos com as importações e os recursos gerados com as exportações em 2009?

a) 600 milhões de dólares.

b) 840 milhões de dólares.

c) 1,34 bilhão de dólares.

d) 1,44 bilhão de dólares.

e) 2,00 bilhões de dólares.

Dica 3 – Melhore sua Memória e o Aprendizado para o Enem e os vestibulares 

Questão 5

(FGV) Simplificando a fração

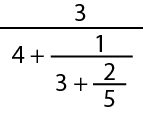obteremos:

a) 51/73

b) 47/69

c) 49/71

d) 45/67

e) 53/75

Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!