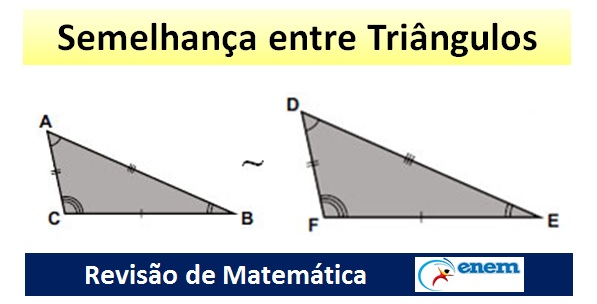
Os Triângulos são semelhantes quando possuem dois ângulos internos iguais. Entenda tudo sobre a Semelhança entre Triângulos nesta aula de Matemática vestibular e Enem. Revisão gratuita com exercícios. Veja abaixo.
Você lembra das aulas sobre Semelhança entre Triângulos? Recorda da expressão ‘Ângulos Congruentes’, e ‘Lados Proporcionais’? É hora de revisar! Cai direto no Enem e nos vestibulares.
Definição de Semelhança entre Triângulos: Dois triângulos são semelhantes se tiverem os ângulos dois a dois congruentes e os lados correspondentes dois a dois proporcionais.
Na prática, pode-se dizer que dois triângulos são semelhantes se um deles é a ampliação ou a redução do outro (da mesma forma como estudado nas escalas na Aula nº 6).
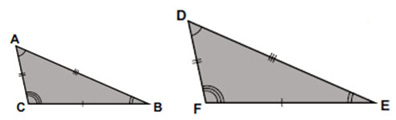
Observe que os triângulos ABC e DEF apresentam os mesmos ângulos; pode-se dizer que o segundo triângulo é a ampliação do primeiro.
Notação: usa-se o símbolo ~ para indicar que os triângulos são semelhantes (![]() ABC ~
ABC ~ ![]() DEF).
DEF).
Existem diversos critérios para o reconhecimento da semelhança entre dois triângulos; o mais comum é o critério dos dois ângulos iguais (conhecido como AA).
Vamos a ele: Dois triângulos são semelhantes se dois ângulos (AA) de um deles são congruentes a dois ângulos do outro.
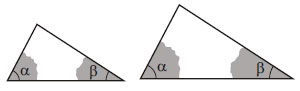
Observe que os triângulos apresentam os mesmos pares de ângulos (α e β). Isso nos leva concluir que o terceiro ângulo desses triângulos são ângulos iguais (congruentes).
Dica 1 – Sabe tudo sobre Triângulo retângulo? Aproveite aqui esta aula sobre Triângulo Retângulo para revisar o conteúdo e garantir uma boa nota na prova de Matemática Enem.
Diz-se então que os triângulos são semelhantes, e como consequência afirma-se que os lados correspondentes são proporcionais.
Veja o exemplo abaixo:
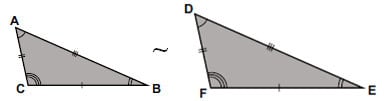
Os lados AB e DE são correspondentes, pois são opostos aos mesmos ângulos; isso também ocorre com os lados AC e DF ou com os lados CB e FE. Aplicando o Teorema de Tales (Aula nº 3), obtém-se:
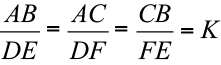
K = Constante de proporcionalidade ou razão de semelhança.
Exemplo: Na figura abaixo o segmento DE é paralelo à base BC, AB = 9 cm, AC = 13 cm, BC = 12 cm e a medida de DE é 8 cm. Determine as medidas dos segmentos AD e AE.
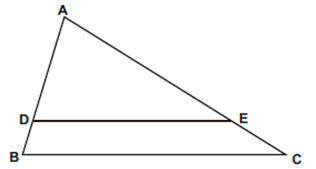
Solução: como o segmento DE é paralelo ao segmento BC, conclui-se que ^B = ^D e ^E = ^C.
Dica 2 – Você sabe a diferença entre um triângulo equilátero e um triângulo escaleno? Então, aproveite para saber tudo sobre Triângulos nesta aula de Matemática Enem
Assim, os triângulos ABC e ADE são semelhantes. Logo:
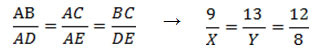
Resolvendo cada igualdade separadamente, encontra-se: AD = X = 6 e AE = Y = 26/3
Importante: Se dois triângulos são semelhantes, a proporcionalidade se mantém constante para quaisquer dois segmentos correspondentes, tais como: lados, medianas, alturas, perímetros, etc.
A semelhança entre triângulos é uma das ferramentas mais importantes da geometria e pode ser aplicada também na solução de problemas envolvendo outros tipos de polígonos, como, por exemplo, os quadriláteros.
Saiba mais sobre Semelhança entre Triângulos com nossa aula
Desafios para você resolver e compartilhar na rede.
Questão 1
Na figura abaixo está representada a fachada de um prédio. Os segmentos de reta [AB] e [CD] são perpendiculares a [BE] e os segmentos de reta [AB] e [CD] são paralelos. Determine a altura deste prédio.
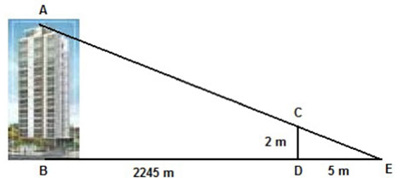
a) 700 m
b) 800 m
c) 900 m
d) 950 m
e) 1.000 m
Questão 2
O jardineiro do Sr. Artur fez um canteiro triangular composto por folhagens e flores onde as divisões são todas paralelas à base AB do triângulo ABC, conforme figura.
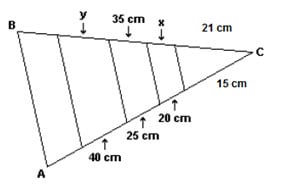
Sendo assim, as medidas x e y dos canteiros de flores são, respectivamente:
a) 30 e 50 cm
b) 28 e 56 cm
c) 50 e 30 cm
d) 56 e 28 cm
e) 40 e 20 cm
Dica 3 – Pronto para gabaritar na prova de Matemática Enem? Relembre sobre definição e aplicações das Figuras Planas em mais esta aula de revisão.
Questão 3
A sombra de uma pessoa que tem 1,80 m de altura mede 60 cm. No momento, a seu lado, a sombra projetada de um poste mede 2 m. Se, mais tarde, a sombra do poste diminui 50 cm, a sombra da pessoa passou a medir:
a) 30 cm
b) 45 cm
c) 50 cm
d) 80 cm
e) 90 cm
Questão 4
Na figura abaixo, o segmento AC é paralelo ao segmento DE. Nessas condições, determine o valor de x + y.
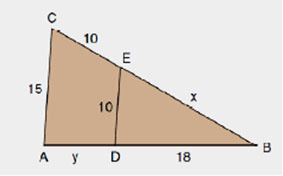
a) 26
b) 27
c) 28
d) 29
e) 30
Questão 5
(ENEM, ano) Um marceneiro deseja construir uma escada trapezoidal com 5 degraus, de forma que o mais baixo e o mais alto tenham larguras respectivamente iguais a 60 cm e a 30 cm, conforme a figura. Os degraus serão obtidos cortando-se uma peça linear de madeira cujo comprimento mínimo, em centímetros, deve ser:
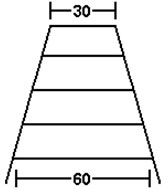
a) 144
b) 180
c) 210
d) 225
e) 240
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!