É conteúdo básico de Matemática. Todo ano têm questões de Função Polinomial do 1º Grau no vestibular e no Enem. Veja aqui revisão com aula gratuita, exercícios resolvidos, e desafios para você responder. Confira abaixo.
É hora de recuperar o conteúdo básico sobre Função Polinomial do 1º Grau. Você sabe como resolver rapidamente questões assim? Caem todo ano no vestibular e no Enem. Vamos lá revisar!
Começando pelo básico. Vamos à descrição do que é uma função Polinomial do 1º Grau: Dados dois conjuntos A e B não vazios, temos que função é a relação onde para cada x pertencente a um conjunto A corresponde a um, e somente um y, pertencente a um conjunto B. Compreendeu o que é uma Função Polinomial?
Compreendeu o que é uma Função Polinomial?
Veja, então, para ajudar você a entender bem certinho, a forma de representação matemática da Função Polinomial do 1º Grau. Temos que uma função polinomial do 1º grau é toda função escrita na forma: ![]()
Vamos aos Exemplos, para você relembrar o conteúdo:
- Veja uma Função Afim:

- Agora, veja uma Função Linear:

Resumo sobre funções
Confira agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, uma aula super focada, simples e rápida, para você dominar funções de uma vez por todas:
Raiz da Função, você lembra o que é?
- É o valor de x que zera a função. Podemos utilizar a seguinte demonstração:

Ponto que intercepta o eixo y
- Temos como valor que intercepta o eixo y (eixo das ordenadas) o coeficiente b. Pois:

Gráfico de Função Polinomial do 1º Grau
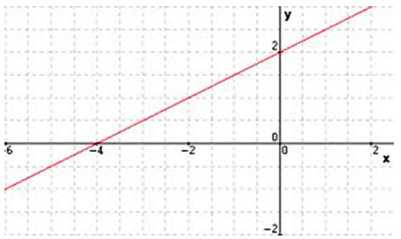
- O gráfico de uma função polinomial do 1º grau é uma reta, com isso precisamos encontrar dois pontos, pois por dois pontos distintos passa uma única reta.

função polinomial do 1º Grau No gráfico acima temos uma função afim, escrita na forma

Classificação das Funções Polinomiais de 1º Grau
- Numa função polinomial do 1º grau
 as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra:
as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra: - Função Crescente: a > 0
- Função Decrescente: a < 0
Exercício Resolvido. Acompanhe o raciocínio!
1. (Ufpr 2012) Numa expedição arqueológica em busca de artefatos indígenas, um arqueólogo e seu assistente encontraram um úmero, um dos ossos do braço humano. Sabe-se que o comprimento desse osso permite calcular a altura aproximada de uma pessoa por meio de uma função do primeiro grau.
- a) Determine essa função do primeiro grau, sabendo que o úmero do arqueólogo media 40 cm e sua altura era 1,90 m, e o úmero de seu assistente media 30 cm e sua altura era 1,60 m.
- b) Se o úmero encontrado no sítio arqueológico media 32 cm, qual era a altura aproximada do indivíduo que possuía esse osso?
- Veja as Respostas das perguntas:
- a) Função do primeiro grau, onde x é o comprimento do úmero e y é a altura do indivíduo.
- b) Portanto, a altura aproximada do indivíduo que possuía esse osso era de 1,66 metros.
Veja um exemplo que caiu nas provas
Acompanhe com o professor Sérgio Sarkis a resolução de questões básicas sobre funções.
Conferiu com o professor Sérgio como não tem mistério? Acompanhe agora no texto outra resolução, que é para você perder o medo.
Mais um Exercício Resolvido:
2. (Ufpb 2011) Em certa cidade, acontece anualmente uma corrida, como parte dos eventos comemorativos pela sua emancipação política. Em 2000, o comitê organizador da corrida permitiu a participação de 1500 pessoas; e, em 2005, a participação de 1800 pessoas. Devido às condições de infraestrutura da cidade, o comitê decidiu limitar o número de participantes na corrida. Nesse sentido, estudos feitos concluíram que o número máximo n(t) de participantes, no ano t, seria dado pela função afim n(t) = at + b, onde a e b são constantes.
- Com base nessas informações, conclui-se que, no ano de 2010, o número máximo de participantes na corrida será de:
- a) 1900
- b) 2100
- c) 2300
- d) 2500
- e) 2700
Veja a Resolução da questão 2:
- Admitindo t = 0 para 2000, t = 1 para 2001, t = 2 para 2002 e assim sucessivamente, temos a seguinte tabela para o número de participantes n(t).
- t n(t)
- 0 1500
- 5 1800
- Da tabela, temos b = 1500 e

- Logo, a função será n(t) = 1500 + 60.t
- Portanto, n(10) = 1500 + 60.10 = 2100
- Gabarito: Alternativa ‘B’
Dica do Blog do Enem: O que mais cai de Matemática
Veja a relação dos conteúdos de matemática que mais caem nas provas do Enem e nos vestibulares mais puxados. A lista foi elaborada pelo professor Carlos Oliveira, do Colégio Bandeirantes, de São Paulo:  Confira na imagem acima a relação dos Temas top ten da Matemática do Enem, com aulas gratuitas.
Confira na imagem acima a relação dos Temas top ten da Matemática do Enem, com aulas gratuitas.
Aula Gratuita – Resumo de Função Polinomial
Saiba mais sobre Função Polinomial nesta aula complementar do professor Sarkis. Depois, responda aos Exercícios sobre Funções.
Exercícios para você resolver e compartilhar
Questão 1
(Unisinos 2012) Qual dos gráficos abaixo representa a reta de equação.
a)
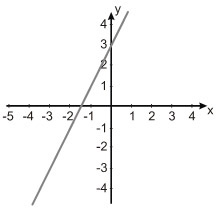
b)
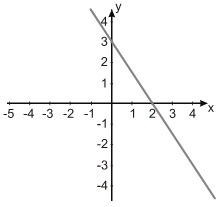
c)
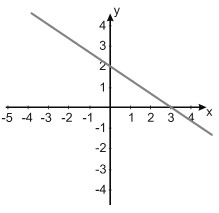
d)
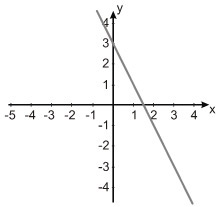
e)
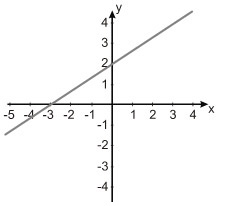
Dica 1 – Acompanhe esta revisão sobre Equações Polinomiais do 1º e 2º grau e fique preparado para a prova de Matemática Enem – https://blogdoenem.com.br/equacoes-polinomiais-1o-e-2o-grau-matematica-enem/
Questão 2
(Enem 2008) A figura a seguir representa o boleto de cobrança da mensalidade de uma escola, referente ao mês de junho de 2008.

Se M(x) é o valor, em reais, da mensalidade a ser paga, em que x é o número de dias em atraso, então
a) M(x)=500+0,4x
b) M(x)=500+10x
c) M(x)=510+0,4x
d) M(x)=510+40x
e) M(x)=500+10,4x
Dica 2 – Revise tudo sobre os Logaritmos em mais esta aula de Matemática Enem, com definições e exercícios resolvidos para você gabaritar no Exame Nacional do Ensino Médio – https://blogdoenem.com.br/logaritmos-matematica-enem-2/
Questão 3
(G1 – cftmg 2008) Na figura, está representado o gráfico da função f(x).
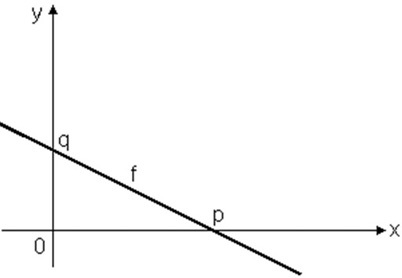
Com relação a f(x) pode-se afirmar que:
I. q representa o termo independente da função f(x).
II. Se x > p, então f(x) < 0.
III. A função f(x) é crescente.
IV. A declividade da reta é dada por p.
Estão CORRETAS somente as afirmativas
a) I e II.
b) I e IV.
c) II e III.
d) III e IV.
Dica 3 – Pronto para o Exame Nacional do Ensino Médio? Revise tudo sobre Função Exponencial em mais esta aula preparatória para a prova de Matemática Enem! – https://blogdoenem.com.br/funcao-exponencial-matematica-enem/
Questão 4
(Ufsm 2006)

Durante o percurso de x km, o Sr. Jones tem o hábito de fazer três paradas de 10 min cada uma. Usando uma velocidade média de 60 km/h, a função que permite calcular o tempo, em horas, que ele leva para percorrer os x km é
a) f(x) = 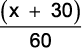
b) f(x) = 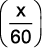 + 30
+ 30
c) f(x) = 6x + 30
d) f(x) = 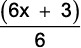
e) f(x) = f(x) = x – 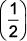
Questão 5
(Pucmg 2004) Em certa cidade, durante os dez primeiros dias do mês de julho de 2003, a temperatura, em graus Celsius, foi decrescendo de forma linear de acordo com a função T(t) = -2t + 18, em que t é o tempo medido em dias. Nessas condições, pode-se afirmar que, no dia 8 de julho de 2003, a temperatura nessa cidade foi:
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!

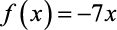
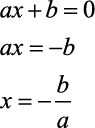
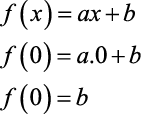
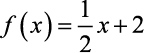
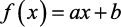 as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra:
as retas poderão ser crescentes ou decrescentes, seguindo a seguinte regra: