O professor Carlos Oliveira, do Colégio Bandeirantes de São Paulo, preparou para você um Plano de Estudos completo com os 10 temas que mais caem em Matemática no Enem. Confira aulas de Razão e Proporção; Regra de Três; Porcentagem; Geometria Plana e Espacial; Gráficos e Tabelas; Equações; e Probabilidade.
A principal dica do professor Carlos Oliveira, coordenador de Matemática do Colégio Bandeirantes, é que fazer as contas não é o principal problema do exame. É claro que precisa saber Regra de Três, Razão, Juros, Geometria e solucionar equações.
Mas, você precisa se preparar para interpretar os problemas e identificar quais são os cálculos de Matemática realmente necessários. Aí é que está o segredo. Bora lá com este Plano de Estudo, porque o Colégio Bandeirantes é um dos dez melhores no Enem de São Paulo. As dicas do professor Carlos são quentes: Sempre caem questões de Razão e Proporção, Cálculo de Juros e Porcentagem, Escala, Gráficos e Tabelas, Equações, Geometria Plana, Geometria Espacial, Estatística, e Probabilidade.
Bora lá com este Plano de Estudo, porque o Colégio Bandeirantes é um dos dez melhores no Enem de São Paulo. As dicas do professor Carlos são quentes: Sempre caem questões de Razão e Proporção, Cálculo de Juros e Porcentagem, Escala, Gráficos e Tabelas, Equações, Geometria Plana, Geometria Espacial, Estatística, e Probabilidade.
10 temas que sempre caem de Matemática no Enem
1. Razão: Normalmente, são problemas que envolvem a divisão em partes proporcionais. Veja uma aula gratuita para mandar bem na prova de matemática do Enem. Clique na imagem:
2. Regra de Três e Proporcionalidade: A prova traz os tradicionais problemas de regra de três (ex.: uma torneira enche um tanque em duas horas e outra enche o mesmo tanque em três horas. Abertas simultaneamente, em quanto tempo ambas as torneiras enchem o tanque?). Clique na imagem para mandar bem na Matemática Enem
3. Porcentagem: Em geral, são problemas de aumentos sucessivos, descontos sucessivos e até mesmo cálculo de variação percentual (decréscimo ou acréscimo).
Dois passos para calcular variação percentual: passo 1, faça a diferença entre valor final e valor inicial. Passo 2: divida o resultado anterior pelo valor inicial. Clique na imagem para mandar bem na Matemática Enem.
4. Interpretação de gráficos e tabelas:
A prova extrai problemas de trechos de revista ou jornal e pede para calcular média, identificar pontos específicos (máximos ou mínimos, por exemplo). Clique na imagem.
Tipos de gráficos e interpretação: Análise gráfica Enem e vestibular
5. Geometria plana:
Sempre tem tópicos clássicos de perímetro, ângulos, lei dos cossenos, teorema de Pitágoras, áreas de regiões poligonais, comprimento da circunferência e área do círculo, triângulos e polígonos regulares. Cai direto na Matemática Enem.
Por isso, para facilitar o estudo dos principais teoremas, use dois lugares ou modos diferentes para fazer as anotações. De um lado (o de um jeito) escreva tudo o que é fornecido no teorema e, do outro, escreva o que você conclui com base nas informações que possui e que você pode usar para resolver a questão.
Diferença entre Hipótese e Tese nos Teoremas – O que é fornecido chama-se hipótese do teorema e o que é concluído é a tese do teorema.
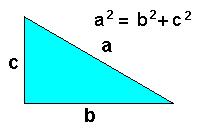
Por exemplo, no Teorema de Pitágoras:
• Hipótese – o triângulo é retângulo (isso é o que tem que ser desenhado).
• Tese – se os lados são “a”, “b” e “c”, “a” sendo o maior, então a²=b²+c². Essa fórmula é o que tem que ser escrito.
Veja aula completa sobre o Triângulo Retângulo e o Teorema de Pitágoras:
6. Equações e sistemas:
todo e qualquer tipo de problema que deve ser reescrito na linguagem algébrica.
7. Geometria espacial:
problemas que demandam o uso das fórmulas dos principais sólidos, a saber, prisma, pirâmide, cilindro, cone e esfera. Dificilmente aparece um sólido inscrito em outro.
Em geral, o problema que cai sobre Geometria Espacial é para calcular o volume de água em uma taça de formato cônico, ou um paralelepípedo, ou algum sólido elementar que seja combinação de um desses. Clique na imagem para esta aula de Matemática Enem.
Geometria Espacial – Aulas e apostilas grátis de Matemática.
8. Progressão Aritmética e Progressão Geométrica
Aprenda as Médias: aritmética e geométrica. Se for dada alguma outra (harmônica, por exemplo) a fórmula será fornecida.
9. Estatística na Matemática Enem:
O básico é saber as fórmulas de medidas de tendência central (média, mediana e moda) e de medidas de dispersão (variância e desvio padrão).
Lista de exercícios sobre média aritmética simples e ponderada
Medidas de Dispersão: a variabilidade dos dados na matemática
10. Contagem e probabilidade:
Os problemas demandam muito mais raciocínio do que fórmulas. Por isso é importante entender profundamente o significado do princípio fundamental da contagem.
Igualmente importante é entender que arranjos são sequências e que combinações são subconjuntos. Isso faz uma tremenda diferença na resolução dos problemas de contagem. Em probabilidade, basta entender o cálculo em espaços equiprováveis para mandar bem na Matemática Enem.
As Dicas de Resolução do professor Oliveira:
Agora que você já sabe quais são as principais abordagens em cada um dos principais temas de matemática, é fundamental se preparar também para a prova em si. Por isso, o Professor Carlos Oliveira reuniu algumas dicas de estudo para matemática:
A – Entenda o problema antes de começar a fazer contas: lembre-se que o cálculo não é o problema. O segredo está em entender qual conta fazer. Para isso, interpretação é fundamental.
B – Tente resolver um mesmo problema com números menores: isso auxilia no entendimento lógico da questão.
C – Identifique seus pontos fracos: procure fazer os últimos exames e tente resolver as questões sem marcar tempo. Anote tudo aquilo em que tem dificuldade. Isso é fundamental para identificar a origem da dificuldade. Com essa informação, você terá mais maturidade e segurança para focar os estudos no que realmente lhe falta.
D – Fique confiante: no dia da prova, todas as questões parecerão “estranhas” em uma primeira olhada, porque são inéditas e contextualizadas. Mas, resgate tudo aquilo que aprendeu no 9º ano e no ensino médio, que conseguirá concluir o exame com êxito.
Por fim, o professor acredita que a boa preparação para o Enem está intimamente ligado a capacidade de o estudante sair da zona de conforto. “Não fique fazendo só aquilo que você já sabe, pois isso não vai acrescentar grande coisa. Tente, resolva, estude aqueles exercícios que você não faria de primeira”, sugere.
Veja também os aulões que o Blog do Enem preparou para ajudar você, na revisão dos conteúdos de Matemática que mais caem no Exame! Assista:
Análise Combinatória
Estatística:
Geometria Plana:
Escalas, Razões e Proporções:




