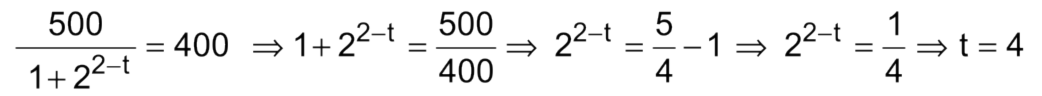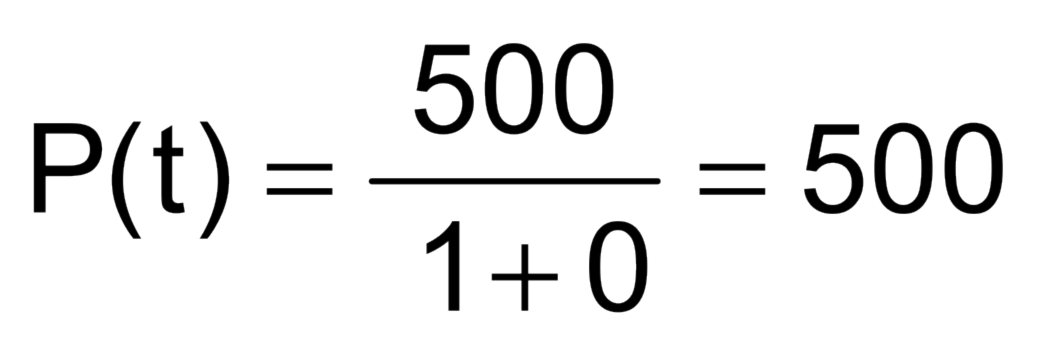Função Exponencial – Aula de Matemática vestibular e Enem.

Função Exponencial – Revisão de Matemática para o Enem. Você lembra?  Vamos lá! Começando pelo começo:  Veja as definições e principais características, e depois veja o Exercício Resolvido.

• Chama-se função exponencial toda função que pode ser reduzida à seguinte forma:
• f(x) = a^x + b,a > 0 e a ≠ 1
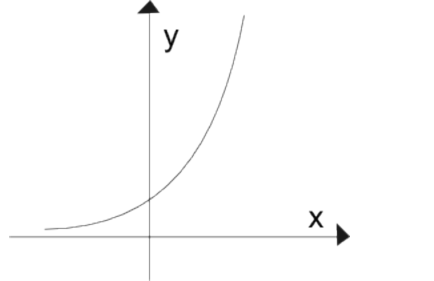
• Veja  nos Gráficos:  Para a > 1, a função é crescente:
• Para 0 < a < 1, a função é decrescente:

Imagem da função:

Para a função f(x)= a^x + b a sua imagem será Im = [b,∞].

Exercício resolvido sobre função exponencial:

(UFPR, 2012) – Um grupo de cientistas decidiu utilizar o seguinte modelo logístico, bastante conhecido por matemáticos e biólogos, para estimar o número de pássaros, P(t), de determinada espécie numa área de proteção ambiental. Sendo t o tempo em anos e t = 0 o momento em que o estudo foi iniciado.

• a) Em quanto tempo a população chegará a 400 indivíduos?
• Resolução:
• 

• b) À medida que o tempo t aumenta, o número de pássaros dessa espécie se aproxima de qual valor? Justifique sua resposta.
• Resolução: Para t muito grande, o valor 2^2-t tende a ser 0; logo, P(t) será dado por
• 
• Portanto, o número de pássaros dessa espécie se aproxima a 500.

Saiba mais sobre Função Exponencial com a aula do prof. Sarkis:

Desafios para você resolver sobre função exponencial

Questão 1

(PUCMG, 2010) O valor de certo equipamento, com- prado por R$ 60.000,00, é reduzido à metade a cada 15 meses. Assim, a equação

V (t) = 60.000 ⋅ ,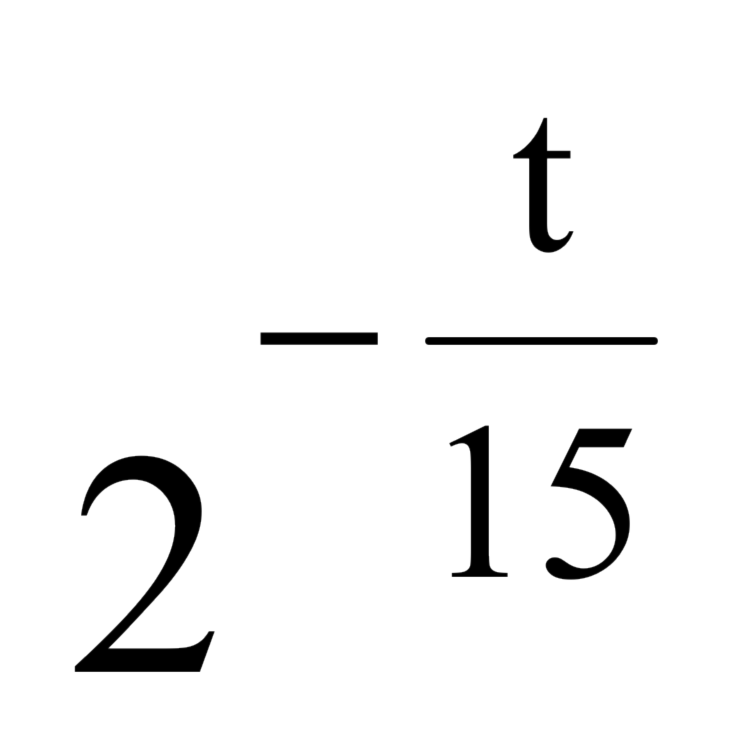

onde t é o tempo de uso em meses e V(t) é o valor em reais, representa a variação do valor desse equipamento. Com base nessas informações, é CORRETO afirmar que o valor do equipamento após 45 meses de uso será igual a:

a) R$ 3.750,00 b) R$ 7.500,00 c) R$ 10.000,00 d) R$ 20.000,00

Dica 1 – O Exame Nacional do Ensino Médio está chegando! Revise sobre Equações Exponenciais para garantir uma boa nota na prova de Matemática Enem – https://blogdoenem.com.br/equacoes-exponenciais-matematica-enem/

Questão 2

(PUCMG, 2007) Uma cultura tem, inicialmente, 125 bactérias. Sabendo-se que essa população dobra a cada 2 horas, o tempo necessário, em horas, para que o número de bactérias chegue a 256.000, é igual a:

a) 14

b) 18

c) 22

d) 26

Dica 2 – Com o Enem chegando você não sabe mais o que estudar? Então, revise sobre Potencialização e Radiciação em mais esta aula de Matemática Enem – https://blogdoenem.com.br/potenciacao-e-radiciacao-matematica-enem/

Questão 3

(ENEM, 2007) A duração do efeito de alguns fármacos está relacionada à sua meia-vida, tempo necessário para que a quantidade original do fármaco no orga- nismo se reduza à metade. A cada intervalo de tempo correspondente a uma meia-vida, a quantidade de fármaco existente no organismo no final do intervalo é igual a 50% da quantidade no início desse intervalo.

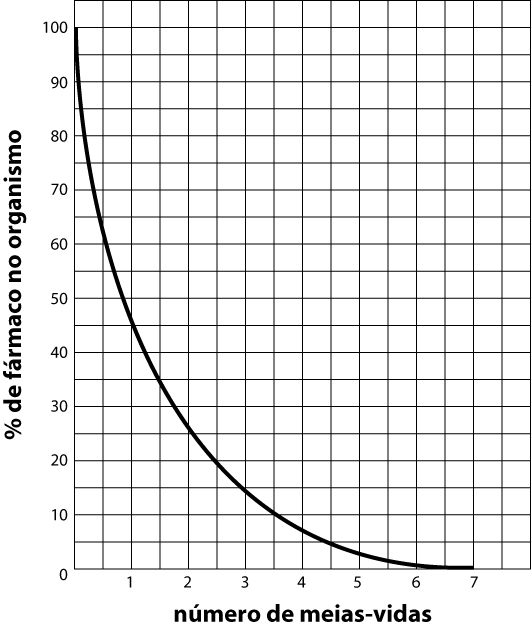
O gráfico anterior representa, de forma genérica, o que acontece com a quantidade de fármaco no organismo humano ao longo do tempo.

Fonte: FUCHS, F. D.; WANNMA, C. I. Farmacologia clinica. Rio de Janeiro: Guanabara Koogan,1992, p. 40.

A meia-vida do antibiótico amoxicilina é de 1 hora. Assim, se uma dose desse antibiótico for injetada às 12 h em um paciente, o percentual dessa dose que restará em seu organismo às 13h30 será aproximadamente de

a) 10%

b) 15%

c) 25%

d) 35%

e) 50%

Dica 3 – Relembre sobre as Equações Racionais e Irracionais em mais esta aula de revisão para a prova de Matemática Enem – https://blogdoenem.com.br/equacoes-racionais-irracionais-matematica-enem/

Questão 4

(UFSM, 2006) Num raio de x km, marcado a partir de uma escola de periferia, o Sr. Jones constatou que o número de famílias que recebem menos de 4 salários mínimos é dado por N(x) = K &#8901 2^2x, onde K é uma constante e x > 0. Se há 6.144 famílias nessa situação num raio de 5 km da escola, o número que você encontraria delas, num raio de 2 km da escola, seria:

a) 2.048

b) 1.229

c) 192

d) 96

e) 48

Questão 5

(UNIRIO, 2002) Numa população de bactérias, há P(t) = 10⁹ ⋅ 4^3t bactérias no instante t medido em horas (ou fração da hora). Sabendo-se que inicialmente existem 109 bactérias, quantos minutos são necessários para que se tenha o dobro da população inicial?

a) 20

b) 12

c) 30

d) 15

e)10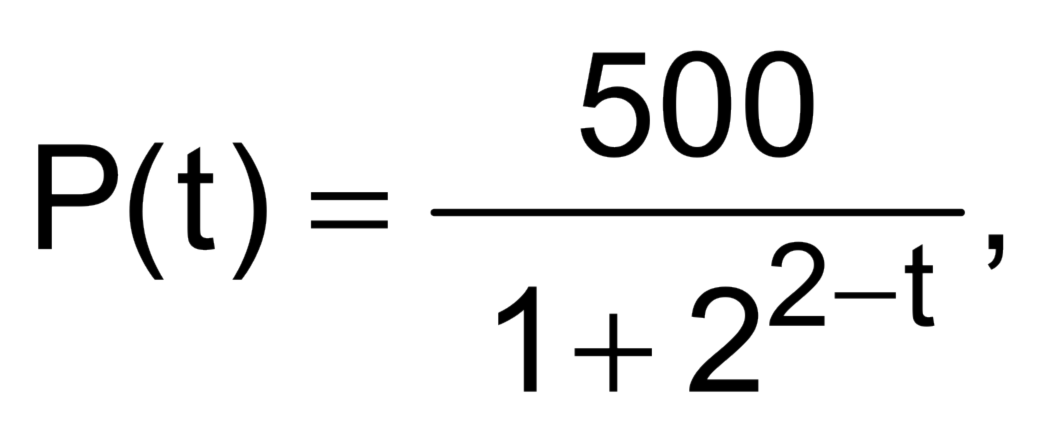

• o: Para t = ? tem-se P(t)=400. Portanto:
•  Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!