Veja as principais fórmulas matemáticas para cálculos sobre Circunferências em mais esta aula de revisão para Enem e Vestibular. Confira abaixo com exercício resolvido.
Revisão sobre os cálculos envolvendo Circunferência. É Geometria Analítica nas questões de Matemática no Enem e no Vestibular. Veja as fórmulas principais, uma aula gratuita, exercício resolvido, e uma bateria de testes para você conferir o seu nível.
Veja a Equação Reduzida da Circunferência: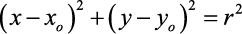
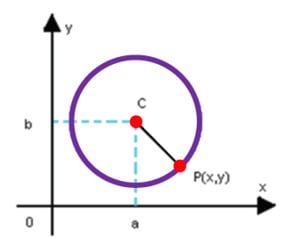
A Equação Geral da Circunferência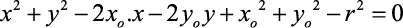
A Distância entre Ponto e Reta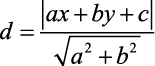
Exercício Resolvido
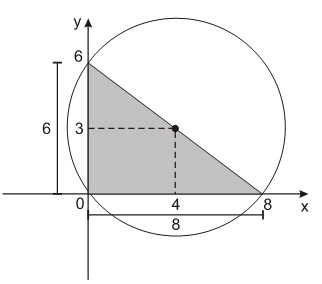
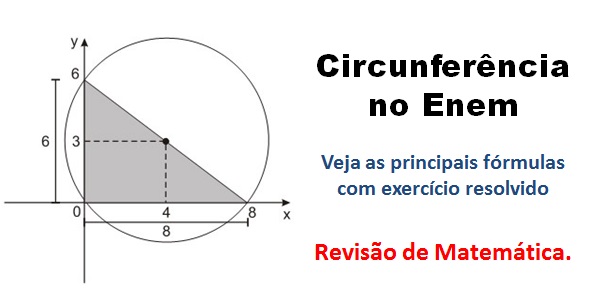
1. (Ufrgs 2010) Os pontos de interseção do círculo de equação (x – 4)2 + (y – 3)2 = 25 com os eixos coordenados são vértices de um triângulo. A área desse triângulo é
- a) 22.
- b) 24.
- c) 25.
- d) 26.
- e) 28
Resolução
- Com o eixo x (y = 0)
- (x – 4)2 + (0 – 3)2 = 25 ⇔ x = 8 ou x = 0 logo os pontos são (0,0) ou (8,0)
- Com o eixo y (x = 0)
- (0-4)2 + (y-3)2 = 25 ⇔ y = 0 ou y = 6, logo os pontos são (0,0) e (0,6)
- Portanto, a área será A =

- Resposta da questão 1: [B]
Aula Gratuita sobre Circunferência – Geometria Analítica
Saiba mais sobre Circunferência nesta aula do canal matematicaemexercicios.com, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
Complicou?
Saiba mais sobre a geometria analítica com nosso primoroso conteúdo disponível no Youtube através do Canal Curso Enem Gratuito! Aqui trazemos uma aula sugerida para você.
Desafios para você resolver e compartilhar a solução
Questão 1
- (Fgv 2010) Dada a circunferência de equação
- x2 + y2 – 6x – 10y + 30 = 0, seja P seu ponto de ordenada máxima. A soma das coordenadas de P e:
- a) 10
- b) 10,5
- c) 11
- d) 11,5
- e) 1
Dica 1 – Preparado para o Exame Nacional do Ensino Médio? Revise tudo sobre Geometria Analítica em mais uma aula de Matemática Enem que preparamos para você – https://blogdoenem.com.br/geometria-analitica-matematica-enem/
Questão 2
(G1 – cftsc 2010) Dada a figura abaixo cujas medidas estão expressas em centímetros,
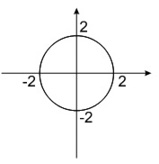 e as proposições:
e as proposições:
- I – é uma circunferência de diâmetro 2 cm.
- II – é uma circunferência de área 4
 cm².
cm². - III – é uma circunferência de equação x² + y² = 4.
- Considerando as proposições apresentadas, assinale a alternativa corretva:
- a) Apenas as proposições I e III são verdadeiras.
- b) Apenas as proposições I e II são verdadeiras.
- c) Apenas a proposição III é verdadeira.
- d) Apenas as proposições II e III são verdadeiras.
- e) Apenas a proposição II é verdadeira.
Dica 2 – Revise sobre as Funções Trigonométricas em mais esta aula preparatória para prova de Matemática Enem. Estude conosco para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/funcoes-trigonometricas-matematica-enem/
Questão 3
(Uft 2010) Considere as equações das circunferências
C1: x2 – 2x + y2 – 2y = 0
C2: x2 – 4x + y2 – 4y = 0
cujos gráficos estão representados abaixo:
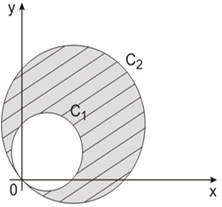
A área da região hachurada é:
a) 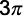 unidades de área.
unidades de área.
b) 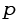 unidades de área.
unidades de área.
c) 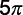 unidades de área.
unidades de área.
d) 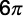 unidades de área.
unidades de área.
e) 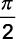 unidades de área.
unidades de área.
Dica 3 – Preparado para o Exame Nacional do Ensino Médio? Revise sobre Trigonometria para garantir a sua nota na prova de Matemática Enem! – https://blogdoenem.com.br/trigonometria-matematica-enem/
Questão 4
(Ufsm 2008) A massa utilizada para fazer pastéis folheados, depois de esticada, é recortada em círculos (discos) de igual tamanho. Sabendo que a equação matemática da circunferência que limita o círculo é
x2 + y2 – 4x – 6y – 36 = 0 e adotando π = 3,14, o diâmetro de cada disco e a área da massa utilizada para confeccionar cada pastel são, respectivamente,
a) 7 e 113,04
b) 7 e 153,86
c) 12 e 113,04
d) 14 e 113,04
e) 14 e 153,86
Questão 5
(Pucrs 2007) A distância entre o centro da circunferência de equação (x – 2)2 + (y + 5)2 = 9 e a reta de equação 2 y + 5 x = 0 é
a) – 5
b) 0
c) 2
d) 5
e) 9
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
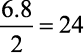
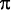 cm².
cm².