Razão e Proporção são assuntos que caem direto no Enem e nos vestibulares. Veja um resumo simples e rápido para você relembrar este conteúdo e resolva os exercícios sobre razão e proporção para não erras nas provas!
Razão e proporção é um conteúdo muito comum no Enem e em todos os vestibulares. Essa tema aparece não só nas questões de Matemática e Física, mas também nas de Geografia, Química e Biologia. Por isso, preparamos um resumo e uma lista de exercícios sobre razão e proporção para você se preparar para as provas.
O que são razão e proporção
A razão entre dois números é simplesmente o quociente entre eles. Por exemplo: suponha que queremos saber a razão entre o número de meninos e meninas em uma sala de aula. Se há 12 meninos e 18 meninas, então a razão entre eles é 12/18.
Simplificando esta fração, fazendo a conta de 12/18, e reduzindo os termos superiores e inferiores por 6, encontramos 2/3. Ou seja: para cada 2 meninos há três meninas.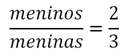
Enquanto isso, a proporção é a igualdade entre razões ou quando razões possuem o mesmo resultado. Portanto, a proporção é a relação entre duas ou mais grandezas.
A fim de que você entenda melhor o significado de proporção, vamos ver a diferença entre grandezas diretamente proporcionais e inversamente proporcionais.
Grandezas diretamente ou inversamente proporcionais
Grandezas diretamente proporcionais são aquelas que variam “no mesmo sentido”. Por exemplo: se uma das grandezas aumenta, a outra também aumenta. Grandezas diretamente proporcionais se relacionam através de divisão.
As grandezas inversamente proporcionais, por sua vez, são aquelas que variam “em sentidos opostos”. Por exemplo, se uma das grandezas aumenta, a outra diminui. Grandezas inversamente proporcionais se relacionam através de multiplicação.
No movimento de um carro, por exemplo, velocidade e distância são exemplos de grandezas diretamente proporcionais. Isso porque quanto maior a velocidade, maior será a distância percorrida. Já velocidade e tempo são grandezas inversamente proporcionais, pois quanto maior a velocidade, menor será o tempo gasto num percurso.
Videoaula sobre razão e proporção
Confira um resumo simples e rápido com o professor Sérgio Sarkis para você dominar os cálculos que envolvem razão e proporção. Ele utiliza exemplos envolvendo área e perímetro de figuras geométricas para você entender o conteúdo e saber resolver exercícios.
Agora que você já sabe como resolver exercícios sobre razão e proporção, treine com as questões que selecionamos! E, depois de conferir o gabarito, não deixe de estudar nosso resumo sobre escalas. Esse é um conteúdo que sempre cai em questões sobre razão e proporção.
Exercícios sobre razão e proporção
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(UEM PR/2014)
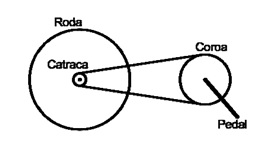
Um modelo padrão para dar movimento a uma bicicleta consiste em duas polias conectadas por uma corrente. Uma das polias, chamada de coroa, fica conectada aos pedais, enquanto a outra polia, chamada de catraca, fica acoplada à roda traseira da bicicleta. Cada pedalada, isto é, cada giro completo dos pedais, corresponde a um giro completo da coroa, enquanto cada volta completa da catraca corresponde a uma volta completa da roda à qual está acoplada. Sabe-se, ainda, que o número de voltas da catraca é proporcional ao número de voltas da coroa, com razão de proporção igual à razão entre os raios da coroa (R) e da catraca (r). Considerando que a bicicleta, a partir do modelo apresentado, desloca-se em linha reta em uma superfície plana e que não haja deslizamento entre as rodas da bicicleta e a superfície, assinale o que for correto.
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 2 de 10
2. Pergunta
(UFG GO/2011)
As imagens a seguir são representativas de períodos históricos e, em cada uma delas, foi destacado um par de medidas.
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 3 de 10
3. Pergunta
(UDESC SC/2010)
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 4 de 10
4. Pergunta
(PUC GO/2010)
Cultura
O girino é o peixinho do sapo
O silêncio é o começo do papo
O bigode é a antena do gato
O cavalo é o pasto do carrapato
O cabrito é o cordeiro da cabra
O pescoço é a barriga da cobra
O leitão é um porquinho mais novo
A galinha é um pouquinho do ovo
O desejo é o começo do corpo
Engordar é a tarefa do porco
A cegonha é a girafa do ganso
O cachorro é um lobo mais manso
O escuro é a metade da zebra
As raízes são as veias da seiva
O camelo é um cavalo sem sede
Tartaruga por dentro é parede
O potrinho é o bezerro da égua
A batalha é o começo da trégua
Papagaio é um dragão miniatura
Bactérias num meio é cultura
ANTUNES, Arnaldo. Cultura. In: Nome. Disponível em: <http:
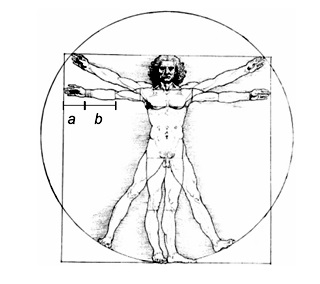
//vagalume.uol.com.br/arnaldo-antunes/cultura. html>. Acesso em: 29 set. 2009.O texto descreve algumas semelhanças entre diversos entes. Um filhote, além de assemelhar-se fisicamente a seu pai, ainda guarda algumas proporções corporais. Tal semelhança pode ser representada matematicamente. Sabe-se que em figuras semelhantes, seus respectivos comprimentos ou grandezas guardam entre si a mesma proporção. A tabela abaixo relaciona algumas grandezas entre um humano adulto de 30 anos, que pesa 64 kg e seu filho de 9 anos, com 38 kg.
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 5 de 10
5. Pergunta
(ENEM/2008)
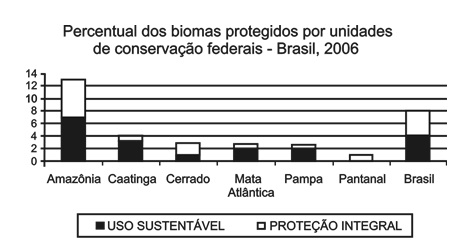
Ministério do Meio Ambiente. Cadastro Nacional de Unidades de Conservação.
Analisando-se os dados do gráfico acima, que remetem a critérios e objetivos no estabelecimento de unidades de conservação no Brasil, constata-se que
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 6 de 10
6. Pergunta
(ENEM/2004)
Já são comercializados no Brasil veículos com motores que podem funcionar com o chamado combustível flexível, ou seja, com gasolina ou álcool em qualquer proporção. Uma orientação prática para o abastecimento mais econômico é que o motorista multiplique o preço do litro da gasolina por 0,7 e compare o resultado com o preço do litro de álcool. Se for maior, deve optar pelo álcool. A razão dessa orientação deve-se ao fato de que, em média, se com um certo volume de álcool o veículo roda dez quilômetros, com igual volume de gasolina rodaria cerca de
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 7 de 10
7. Pergunta
(UNCISAL/2017)
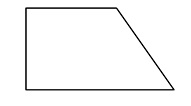
A figura apresenta um esboço (desenhado sem escala) da planta do terreno, na forma de um trapézio retângulo, onde vai ser construído o novo campus de uma universidade estadual.
Se ele mede 4,0 km de frente, 7,0 km de fundos e 5,1 km de frente a fundos pelo lado ortogonal aos fundos, o terreno mede de frente a fundos pelo lado “não ortogonal”, aproximadamente,
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 8 de 10
8. Pergunta
(IFMA/2016)
Em um mapa, construído numa escala de 1:500000, a distância entre duas cidades, A e B, é 80 cm. Qual a distância real entre elas?
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 9 de 10
9. Pergunta
(ENEM/2016)
Num mapa com escala 1 : 250 000, a distância entre as cidades A e B é de 13 cm. Num outro mapa, com escala 1 : 300 000, a distância entre as cidades A e C é de 10 cm. Em um terceiro mapa, com escala 1 : 500 000, a distância entre as cidades A e D é de 9 cm. As distâncias reais entre a cidade A e as cidades B, C e D são, respectivamente, iguais a X, Y e Z (na mesma unidade de comprimento). As distâncias X, Y e Z, em ordem crescente, estão dadas em
Correto
Parabéns! Siga para a próxima questão.
-
Pergunta 10 de 10
10. Pergunta
(UNCISAL/2015)
A figura (desenhada sem escala) apresenta uma piscina circular, em torno da qual há um deck, também circular, protegido por grades de ferro que o tangenciam.
Se os comprimentos das grades AB, AC e BD são respectivamente iguais a 6 m, 9 m e 10 m, o comprimento da grade CD é
Correto
Parabéns! Siga para a próxima questão.
Resumo sobre escalas
Quando se constrói uma escala, deve-se considerar o tamanho real do que você quer representar e também o tamanho da figura que o representará. Estes tamanhos devem estar na mesma unidade de medida, respeitando a razão e a proporção.
Por exemplo: uma casa que possui um comprimento de 20 metros deve ser representada em um desenho de no máximo 20 cm.
Vemos que as unidades de medida não são as mesmas. Portanto, vamos transformar o metro em cm, pois é nesta unidade que representaremos o desenho, 20 metros = 2000 centímetros.
A escala é simplesmente a razão entre o tamanho do desenho e o tamanho real.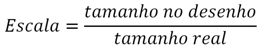 
Assim, para o nosso exemplo:
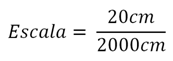
Simplificando por 20 o numerador e o denominador e também a unidade de medida, encontramos a escala: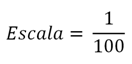
Ela significa que cada centímetro no desenho representa 100 centímetros no real.
Escala numérica
A escala numérica: é representada por uma fração 1 / 10.000 ou por uma razão 1:10.000.
Nessa representação, teremos que cada 1 unidade de medida no desenho corresponde a 10.000 unidades de medida na realidade.
Assim, se em um mapa a escala for de 1: 10.000, teremos que cada 1 cm medido no mapa corresponde à medida de 10.000 cm, ou seja, 100 metros.
Outro exemplo: escala 1: 250 (cada 1 unidade de medida no mapa corresponde na realidade a 250 unidades de medida)
Escala gráfica
Uma escala gráfica é representada por um segmento de reta graduada em uma unidade de medida linear, dividida em partes iguais indicativas da unidade utilizada.
A primeira parte, denominada como talão ou escala fracionária, é subdividida de modo a permitir uma avaliação mais detalhada das distâncias ou dimensões no mapa.
Por exemplo: na escala 1: 100 000, “1 cm” representa a distância no mapa, enquanto que o “100.000 cm” representa a distância real. Isso significa que 1 cm no mapa corresponde a 100.000 cm na realidade, ou seja, 1 km.
Videoaula sobre escalas
Para finalizar seus estudos sobre escalas, razão e proporção, confira nossa videoaula:
