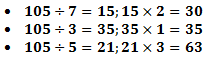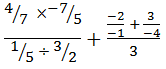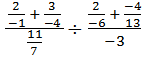É hora de recuperar um conteúdo básico para o ENEM e os vestibulares: as temidas e mal compreendidas. Mas, é bem simples. Veja como somar, subtrair, multiplicar e dividi-las para mandar bem. Confira!
Para começo de conversa, para você aprender de maneira simples e descomplicada, entenda que uma ‘fração’ significa uma parte de um todo. Por exemplo, para resolver Operações com Frações, pense que 1/4 (um quarto) tem a significação direta de 0,25, que nada mais é do que a “quarta parte de um”. Temos, então, que : 1/4 = 0,25
- Mas, na Fração Algébrica temos no denominador pelo menos uma incógnita a ser desvendada (para ser resolvida).
- Então, a nossa Fração Algébrica, partindo do exemplo inicial de fração, seria, por exemplo 1/x = 0,25.
- E, A incógnita a ser descoberta ao resolver a conta é o ‘x’ da questão. Neste caso, x = 4
Operações com Frações
Esse tipo de expressão é muito utilizado na geometria, por exemplo, para representar áreas, perímetros e volumes de figuras ou objetos que possuem dimensões algébricas.
Veja uma síntese sobre as Operações com Frações Algébricas e as regras que precisam ser respeitadas para que a equação seja válida e que possa ser resolvida. O denominador (a parte de baixo) nunca pode ser zero, pois não há divisão por zero.
Introdução às Frações
Veja agora com o professor Lucas borguesan, do canal do Curso Enem Gratuito, uma introdução básica para você resolver as frações mais simples. todo ano elas caem nas provas.
As dicas do professor Lucas:
- Questões envolvendo frações no Enem são consideradas de nível básico.
- Mas, o que são frações? SAs frações são a representação de partes em que um todo foi dividido.
- Porém, uma fração também pode representar uma divisão, na qual o numerador corresponde ao dividendo e o denominador equivale ao divisor.
- Ou, ainda, pode ser considerada como um número racional.
- Tire suas dúvidas no vídeo acima.
A Representação de Fração
As frações são constituídas de duas partes, o numerador e denominador:
Uma fração é uma maneira de representar um número por uma divisão, na qual o numerador está sendo dividido pelo denominador.
Somar frações quando o denominador é igual é muito fácil, acompanhe:
Viu como dá pra resolver praticamene “de cabeça~as Operações com Frações mai simples? – É básico demais: se o denominador é comum a todas as frações, basta somar os numeradores que estão na parte de cima, e copiar (repetir) o denominador, que está prontinho.
O grande problema é quando os denominadores são diferentes. E aí, como fazemos? Tem solução, sim. Acompanhe no vídeo, e depois contnue nesta aula.
Resumo sobre Operações com Frações
Veja com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, como dá sim pra aprender de maneira descomplicada e gabaritar nas questões de Frações:
Viu só como não tem mistério?
Resolução de Operações com Frações
Veja abaixo o exemplo com denominadores diferentes:
Como resolver:
1)Ache o MMC dos denominadores 7, 3 e 5.
2) Para cada uma das frações divida o MMC que você encontrou pelo denominador e depois multiplique pelo numerador.
3) Some ou subtraia os números obtidos pelo passo 2, respeitando a operação que o exercício pedir, então esse será o numerador da sua soma, o denominador será o MMC do passo 1.
Dicas do Blog do Enem:
Dica 1: Veja uma aula básica de fração. do Curso Enem Gratuito
Para continuar mandado bem esta aula com o resumo de Operações com Frações, confira este vídeo do professor Sérgio Sarkis, do canal do Curso Enem Gratuito!
Veja, agora, numericamente :
1) Ache o MMC dos denominadores, MMC(3,5,7) = 105
2) Para cada uma das frações divida o MMC que você encontrou pelo denominador e depois multiplique pelo numerador:
3) Some os números obtidos:
E ai? Entenderam mais essa dica pro Enem? Já a multiplicação e a divisão de frações é muito mais fácil, confira:
Sim, é muito fácil, basta multiplicar numerador com numerador e denominador com denominador, simples não? Notem que:
Chamamos esse processo de simplificação de frações que consiste em eliminar os fatores comuns do numerador e do denominador – em nosso caso, o fator 2. Show né? Fique com a gente e seja nosso aluno nota 1000.
A divisão de frações é tão simples quanto a multiplicação:
Todos nós sabemos que o processo de divisão é o inverso da multiplicação, portanto vamos transformar nossa divisão em uma multiplicação invertendo o segundo termo da nossa conta. Confira:
Outra coisa interessante de se perceber é que fração é apenas uma maneira de representar um número, por exemplo, o número abaixo.
A fração 
é chamada de fração decimal pois tem no denominador um múltiplo de 10.
Para que você fixe esses conteúdos sobre frações, veja a seguinte aula do professor Paulo Vicente sobre como somar frações. As frações irão aparecer em diversas áreas, desde a Ciência da Natureza até a própria Matemática.
Frações e Porcentagem
Veja agora como é simples para você transformar Frações em Porcentagem. É um tipo de questão que aparece direto nas provas do Enem e dos vestibulares.
Gostaram galera? Na próxima aula vamos falar mais sobre números decimais. É essencial que esses assuntos estejam fixados para que vocês arrasem no Enem e para isso, que tal fazer uns exercícios. Vamos lá, estude com o Blog e saia bem na prova.
EXERCÍCIOS:
Dois exercícios básicos pra testar o conhecimento de vocês.
1) 
2) 
RESPOSTAS:
