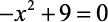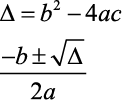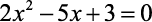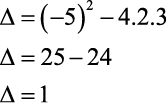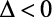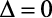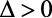Veja nesta aula de Matemática Enem o Estudo do Delta, da Equação Polinomial do 2º grau, e como resolver as questões com a Fórmula de Bhaskara. Agora, no resumo gratuito:
Você lembra das aulas sobre Equação Polinomial do 2º grau? Se já esqueceu, não tem mistério. Veja a fórmula de Bhaskara e o resumo a seguir para recuperar este conteúdo. Vem com calma que dá para relembrar e aprender pra gabaritar nas questões de Matemática.
– Polinômios caem sempre. Mesmo que não apareçam ‘questões puras’ de Equações Polinomiais o raciocínio utilizado na resolução dos Polinômios de 1º grau ou dos Polinômios de 2º grau está presente na forma de resolver questões em diversas outras disciplinas que demandam raciocínio matemático.
A Fórmula de Bhaskara
Confira com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, os macetes para você resolver bem rápido as questões com as equações de 2º grau.
Então, gostou do resumo inicial sobre a F’romula de Bhaskara? Fique de olho e treine as Equações Polinomiais, pois vão além das questões da prova de Matemática. Vamos lá?
O que é uma Equação Polinomial do 1º grau, e o que são as equações do 2º grau? – Resposta fácil de você entender e nunca mais esquecer:
- Uma equação polinomial de 1º grau é uma sentença matemática onde temos uma igualdade entre os dois lados, e que envolve números desconhecidos representados por letras.
- Temos que equação polinomial do 1º grau é toda equação que pode ser escrito na forma:

Exemplos de equações polinomiais:
a) ![]()
b) 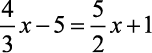
Veja como resolver equações de 1º grau
Equação Polinomial do 2º grau, e a Fórmula de Bháskara
Agora o grau de complexidade sobe um pouco. Então, temos que equação polinomial do 2º grau é toda equação que pode ser escrita na forma: 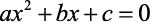
- Definição de Equação Polinomial do 2º Grau: Temos que uma equação polinomial do 2º grau é toda equação escrita na forma:

- Exemplos:
- a)
 , e
, e - b)

- A Fórmula de Bhaskara:
- Dentre as várias maneiras de solucionar uma equação polinomial do 2º grau, temos como a mais comum e mais utilizada as fórmulas de delta e Bhaskara. Confira:

Veja o exemplo para encontrar a solução da equação

- Temos a=2, b=-5 e c=3
- Assim, acompanhe com atenção:
.
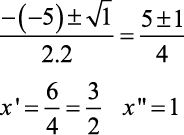
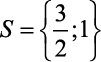
Veja como resolver com a Fórmula de Bhaskara:
Aprenda com o professor Sérgio Sarkis a resolver as questões de prova com a fórmula mais popular das equações do segundo grau.
Gostou do resumo do professor Sérgio Sarkis sobre Equação do 2º Grau e a Fórmula de Bhaskara? Muito boa a didática dele. Veja mais aulas de revisão de matemática no canal do Curso Enem Gratuito.O Estudo do Delta
O delta nos criará três situações distintas na resolução de uma equação, vamos a elas:
- Para

- Não teremos raízes Reais.
- Para

- Teremos duas raízes Reais e Iguais.
- Para

- Teremos duas raízes Reais e Distintas.
Soma e Produto das Raízes
Para as equações polinomiais poderemos utilizar a relação de Girard, que para as equações de 2º grau será conhecida como “soma e produto”.
Vamos a elas: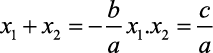
Exercício Resolvido
(Ufpr 2011) Durante o mês de dezembro, uma loja de cosméticos obteve um total de R$ 900,00 pelas vendas de um certo perfume. Com a chegada do mês de janeiro, a loja decidiu dar um desconto para estimular as vendas, baixando o preço desse perfume em R$ 10,00. Com isso, vendeu em janeiro 5 perfumes a mais do que em dezembro, obtendo um total de R$ 1.000,00 pelas vendas de janeiro. O preço pelo qual esse perfume foi vendido em dezembro era de:
a) R$ 55,00.
b) R$ 60,00.
c) R$ 65,00.
d) R$ 70,00.
e) R$ 75,00.
Gabarito: [B]
Sejam  e
e 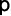 , respectivamente, o número de perfumes vendidos e o preço unitário do perfume em dezembro. Desse modo,
, respectivamente, o número de perfumes vendidos e o preço unitário do perfume em dezembro. Desse modo,
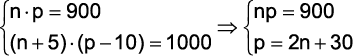
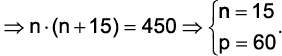
Aula Gratuita sobre como resolver Equações
Os 10 Temas de Matemática que mais caem no Enem
Aulas gratuitas e Simulados Online para você revisar Razão e Proporção; Regra de Três; Porcentagem; Geometria Plana e Espacial; Gráficos e Tabelas; Equações; e Probabilidade. Acesso gratuito aqui:  Regra de Três; Cálculo de Área e de Perímetro; Juros Simples e Juros Compostos; Triângulos; Quadriláteros; Equações; Progressão Aritmética e Progressão Geométrica; Trigonometria. Veja aqui o que mais cai.
Regra de Três; Cálculo de Área e de Perímetro; Juros Simples e Juros Compostos; Triângulos; Quadriláteros; Equações; Progressão Aritmética e Progressão Geométrica; Trigonometria. Veja aqui o que mais cai.
Desafios sobre a Fórmula de Bhaskara
Questão 1 – Equações do segundo grau
Quanto à equação 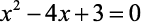 é correto afirmar que:
é correto afirmar que:
- a) a soma de suas raízes é igual a 4.
- b) tem duas raízes reais e iguais.
- c) tem duas raízes reais e distintas.
- d) não tem raízes reais.
- e) o produto de suas raízes é nulo.
Dica 2 – Pronto para gabaritar na prova de matemática do Enem? Faça uma revisão com esta aula sobre Equações Polinomiais do 1º grau – https://blogdoenem.com.br/equacoes-polinomiais-1o-grau-matematica-enem/
Questão 2
- Quarenta pessoas em excursão pernoitaram em um hotel.
- Somados, os homens despendem R$2400,00. O grupo de mulheres gasta a mesma quantia, embora cada uma tenha pago R$ 64,00 a menos que cada homem.
- Denotado por x o número de homens do grupo, uma expressão que modela esse problema e permite encontrar tal valor é:
- a) 2400x=(2400+64x).(40-x)
- b) 2400.(40-x)=(2400-64x)
- c) 2400x=(2400-64x).(40-x)
- d) 2400.(40-x)=(2400+64x).x
Dica 3 – Já sabe tudo sobre Conhecimentos Geométricos? Revise com esta aula sobre Escalas e fique pronto para a prova de Matemática do Enem – https://blogdoenem.com.br/escalas-matematica-enem/
Questão 3
A adição de um número real positivo x com o seu quadrado dá um resultado igual a 42. Então esse número é:
- a) Ímpar
- b) é maior que 15
- c) é múltiplo de 3
- d) é menor que 5
Questão 4
Se A e B são as raízes de 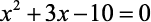 , então
, então 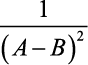
vale:
a) 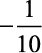 b)
b) 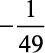 c)
c) 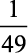
d) 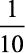 e)
e) 
Questão 5
(G1 – utfpr 2010) Resolvendo a equação biquadrada 6x4 – 5x2 + 1 = 0, obtém-se:
a) 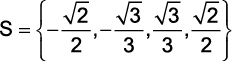
b) 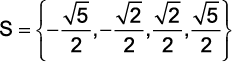
c) 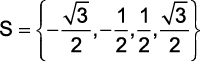
d) 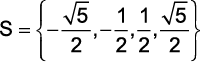
e) 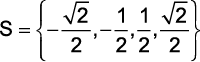
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!

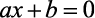
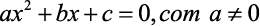
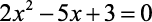 , e
, e