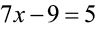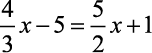Equações do 1º Grau: veja como resolver polinômios. Ensino Médio & Enem

Vamos começar pelo básico do básico. Você sabe o que é uma Equação?  Bem simples e direto aqui, com três cores representando os elementos essenciais de uma equação: Equação é uma sentença matemática onde temos uma igualdade e envolve números desconhecidos representados por letras.

Então, observe a proposição matemática no quadro abaixo e perceba que ela tem todos os elementos essenciais: É uma sentença matemática; Contempla a igualdade entre os dois lados; e envolve números desconhecidos.

Confira abaixo como se escrevem e como se resolvem as equações polinomiais de 1º grau: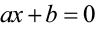

• Veja dois exemplos de Equações de 1º Grau:
•  
• 

Aula Gratuita sobre Equações do Primeiro Grau

Agora, veja como resolver equações do Primeiro Grau. Aula bem focada com o professor Sérgio Sarkis, do Curso Enem Gratuito. Ele explica no passo a passo como você pode chegar lá. Confira e depois veja os exercícios resolvidos e teste seu nível no Simulado Enem.

Veja o que é a Raiz da Equação

Raiz da Equação é o valor que numérico que ao substituir à incógnita (letra que representa o valor desconhecido) torna a igualdade verdadeira. Para o caso das equações polinomiais do 1º grau temos: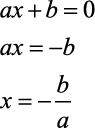

Exercícios Resolvidos

Encontrar a raiz das equações abaixo para U=Q.

a)

.

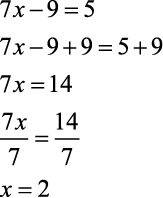
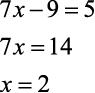
b)

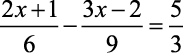
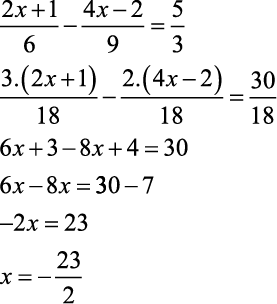
Agora, resoluções com Sérgio Sarkis

Veja um resumo simples e rápido com resolução de problemas:

Muito bom o professor Sarkis!

 Agora, mais um Exercício resolvido

(Ueg 2012) Em uma sala de cinema com 100 lugares, o valor do ingresso inteira custa R$ 20,00, enquanto o valor da meia-entrada custa 50% da inteira. Em uma seção, em que foram vendidos 80 meias e 20 inteiras, o faturamento foi de R$ 1.200,00. Se o proprietário da sala der um desconto de 20% no valor da entrada, qual deve ser o número de pagantes com meia- entrada para que o proprietário tenha a sala cheia e o mesmo faturamento da seção anterior?

• a) 80
• b) 50
• c) 40
• d) 20

Gabarito: B

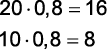
X é o número de Pagantes com meia entrada.

100 – x é o número de pagantes com entrada inteira.

Temos, então, a seguinte equação:

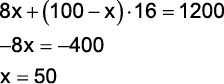
Simulado Enem  – Teste aqui o seu nível nas Equações do Primeiro Grau:

Desafios para você resolver e compartilhar

Questão 1

Determine a solução da equação

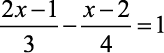para U=Q

Dica 1 – Já sabe tudo sobre Conhecimentos Geométricos? Revise com esta aula sobre Escalas e fique pronto para a prova de Matemática do Enem – https://blogdoenem.com.br/escalas-matematica-enem/

Questão 2

(Enem 2010) Uma escola recebeu do governo uma verba de R$ 1000,00 para enviar dois tipos de folhetos pelo correio. O diretor da escola pesquisou que tipos de selos deveriam ser utilizados. Concluiu que, para o primeiro tipo de folheto, bastava um selo de R$ 0,65 enquanto para folhetos do segundo tipo seriam necessários três selos, um de R$ 0,65, um de R$ 0,60 e um de R$ 0,20.

O diretor solicitou que se comprassem selos de modo que fossem postados exatamente 500 folhetos do segundo tipo e uma quantidade restante de selos que permitisse o envio do máximo possível de folhetos do primeiro tipo.

Quantos selos de R$ 0,65 foram comprados?

• a) 476
• b) 675
• c) 923
• d) 965
• e) 1 538

Dica 2 – Entenda como converter as unidades de medida de Comprimento e Área em mais esta aula de Matemática Enem – https://blogdoenem.com.br/volume-capacidade-matematica-enem/

Questão 3

(Enem 2010) O Salto Triplo é uma modalidade do atletismo em que o atleta dá um salto em um só pé, uma passada e um salto, nessa ordem. Sendo que o salto com impulsão em um só pé será feito de modo que o atleta caia primeiro sobre o mesmo pé que deu a impulsão; na passada ele cairá com o outro pé, do qual o salto é realizado.

Um atleta da modalidade Salto Triplo, depois de estudar seus movimentos, percebeu que, do segundo para o primeiro salto, o alcance diminuía em 1,2 m, e, do terceiro para o segundo salto, o alcance diminuía 1,5 m. Querendo atingir a meta de 17,4 m nessa prova e considerando os seus estudos, a distância alcançada no primeiro salto teria de estar entre:

• a) 4,0 m e 5,0 m.
• b) 5,0 m e 6,0 m.
• c) 6,0 m e 7,0 m.
• d) 7,0 m e 8,0 m.
• e) 8,0 m e 9,0 m.

Dica 3 – Revise as noções de Comprimento e Área com esta aula sobre Unidades de Medidas para a prova de Matemática Enem – https://blogdoenem.com.br/comprimento-e-area-matematica-enem/

Questão 4

(Enem 2009) Um grupo de 50 pessoas fez um orçamento inicial para organizar uma festa, que seria dividido entre elas em cotas iguais. Verificou-se ao final que, para arcar com todas as despesas, faltavam R$ 510,00, e que 5 novas pessoas haviam ingressado no grupo. No acerto foi decidido que a despesa total seria dividida em partes iguais pelas 55 pessoas. Quem não havia ainda contribuído pagaria a sua parte, e cada uma das 50 pessoas do grupo inicial deveria contribuir com mais R$ 7,00.

De acordo com essas informações, qual foi o valor da cota calculada no acerto final para cada uma das 55 pessoas?

• a) R$ 14,00.
• b) R$ 17,00.
• c) R$ 22,00.
• d) R$ 32,00.
• e) R$ 57,00.

Questão 5

(Enem 2004) Em quase todo o Brasil existem restaurantes em que o cliente, após se servir, pesa o prato de comida e paga o valor correspondente, registrado na nota pela balança. Em um restaurante desse tipo, o preço do quilo era R$12,80. Certa vez a funcionária digitou por engano na balança eletrônica o valor R$18,20 e só percebeu o erro algum tempo depois, quando vários clientes já estavam almoçando. Ela fez alguns cálculos e verificou que o erro seria corrigido se o valor incorreto indicado na nota dos clientes fosse multiplicado por:

• a) 0,54
• b) 0,65
• c) 0,70
• d) 1,28
• e) 1,42

 Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!