Relembre as técnicas e os macetes sobre como resolver rápido as Equações Racionais e Irracionais em mais esta aula de revisão para a prova de Matemática Enem
Você vai aprender agora nesta aula qual é diferença básica entre as Equações Racionais e uma Equação Fracionária. A Equação Racional é aquela onde o “x” da questão está na parte de baixo da fração.
Na prática, é onde a “letra” que representa a variável, está colocada com o o denominador. Por exemplo: 2/x = 5 (dois sobre “xis”) é igual a cinco. Veja no vídeo como o professor ajuda você a resolver, e encontra o valor de “x”.
Cai sempre assim a forma básica de representação das Equações Racionais nas provas do Enem. Este é um tipo que sempre cai.
Mas, você também pode encontrar Equações Racionais onde o denominador fica mais “esquisito”…. O professor Lucas explica no vídeo que o denominador pode ter dois termos.
Como resolver Equações Racionais
Por exemplo: 3/x+2 = 3 (três sobre “xis” mais dois, é igual a três). Aprenda no vídeo agora, do canal do Curso Enem Gratuito, como resolver essa equação racional.
Tudo começa com Função e Equação Racional. Depois vêm Domínio, Raízes e Representação. Vamos lá:
Uma equação racional pode ser definida como uma equação na qual figure a razão entre polinômios.
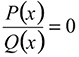
Como calcular o Mínimo Múltiplo Comum
Para ajudar a você a resolver as Equações Racionais é importante fazer uma revisão sobre Mínimo Múltiplo Comum. Confira agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito.
Exercício resolvido:
(UFPE, 2011) Sabendo que , assinale
.
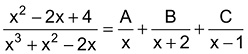Resolução:
Tem-se que
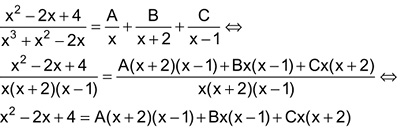
Fazendo x = -2 obtém-se
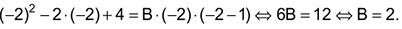
Para x=1 encontra-se
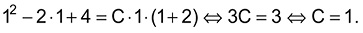
Finalmente, para x=0 vem
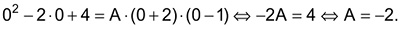
Portanto, A + B + 2C = -2 + 2 + 2 ⋅ 1 = 2.
Equação irracional
Equação irracional é uma equação em que há incógnita em um ou mais radicais.
São equações irracionais:
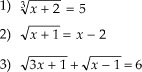
Exercício resolvido:
(PUC-RIO, 2008) O número de soluções da equação x =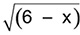 
, com x > 0, é igual a:
a) 0
b) 1
c) 2
d) 3
e) 4
Gabarito: B
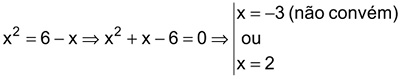
Como resolver Inequações no Enem
Veja agora os macetes de matemática para você gabaritar nas questòes de Inequações.
Desafios sobre Equações Racionais
Questão 1
(UFG, 2005) Sendo x ∈ R, x ≠ 1, encontre os valores de A, B e C, para os quais vale a decomposição:
x/[(x – 1)(x2 + 1)] = [A/(x – 1)] + [(Bx + C)/(x2 + 1)]
a) A = C = 1/2 e B = -1/2
b) A = 3/2; B = -1/2 e C = 1/2
c) A = 7; B = 1 e C = 2/3
d) A = -1; B =1 e C = 2
Dica 1 – Relembre as funções e propriedades dos Polinômios nesta aula de revisão para Matemática Enem – https://blogdoenem.com.br/polinomios-matematica-enem/
Questão 2
(UFC, 2004) Se a expressão (2x + 5)/(4x2 – 1) = [a/(2x + 1)] + [b/(2x – 1)], onde a e b são constantes, é verdadeira para todo número real x ≠ ±1/2, então o valor de a + b é:
a) -2
b) -1
c) 1
d) 2
e) 3
Dica 2 – Revise os Paralelogramos nesta aula de Quadriláteros para a prova de Matemática Enem. Estude conosco para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/paralelogramos-matematica-enem/
Questão 3
Resolver: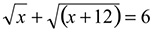
a) V = {1}
b) V = {2}
c) V = {3}
d) V = {4}
e) V = {5}
Dica 3 – Você sabe o que é um Trapézio? Se você ainda não o estudou, aproveite esta aula de Matemática Enem e saiba tudo sobre os Quadriláteros e suas definições – https://blogdoenem.com.br/quadrilateros-matematica-enem/
Questão 4
No conjunto R, o conjunto verdade da equação
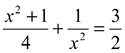é:
a) V = {4, -4, 1, -1}
b) V = {2, -2, 1, -1}
c) V = {4, -4}
d) V = {1, -1}
e) V = {4, -4, 2, -2}
Questão 5
(G1 – UTFPR, 2007) Adriana e Gustavo estão participando de uma gincana na cidade de Curitiba e receberam a seguinte tarefa:
Trazer a fotografia da construção localizada na rua XV de Novembro, número N, tal que:
a e b são as raízes da equação irracional
;
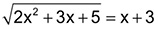N = (a2 + b2 + 13)2 + (a + b) 4 – 10.
a) 1.515
b) 1.296
c) 971
d) 775
e) 535
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
