Relembre as funções e propriedades dos Polinômios em mais esta aula de revisão para a prova de Matemática Enem. Veja exercícios resolvidos para não esquecer como solucionar questões assim nas próximas provas. Confira abaixo.
Veja agora os Polinômios, e domine as Funções e Propriedades para gabaritar Matemática no Enem e no Encceja. É hora de revisar. Sempre cai nas provas. São questões fáceis, que não dá para errar. Veja o resumo para você também mandar bem:
Comece pelo princípio. Veja a definição do que é uma função polinomial: Pode-se definir como função polinomial (ou equação polinomial), as funções escritas na seguinte forma:![]()
Para você compreender melhor, pense o seguinte: ‘Poli’ quer dizer ‘muitos’. ‘Monômios’ quer dizer ‘termos’. Então, um polinômio é caracterizado por conter uma série de termos (ou monômios) expressos em forma matemática. Eles integram uma função polinomial.
Funções e Propriedades dos Polinômios
Veja agora com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, as Funções e Propriedades dos Polinômios para você dominar o básico e resolver com tranquilidade as questões do Enem.
O Grau de um polinômio
O grau de um termo de uma variável em um polinômio é o expoente dessa variável nesse termo. Por exemplo, em 2x³ + 4x² + x + 7, o termo de maior grau é 2x³; esse termo, e, portanto, todo o polinômio, é dito ser de grau 3.
Os Polinômios Idênticos
São polinômios de mesmo grau, que possuem os coeficientes correspondentes iguais.
Operações com Polinômios
Adição e Subtração – Considere os polinômios –2x² + 5x – 2 e –3x³ + 2x – 1. Vamos efetuar a adição e a subtração entre eles.
Veja como fazer a Adição
- (–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
- –2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes
- –2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência
- –3x³ – 2x² + 7x – 3
Veja como fazer a Subtração
- (–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal
- –2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes
- –2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência
- 3x³ – 2x² + 3x – 1
Resumo sobre Operações com Polinômios
Veja com o professor Sérgio Sarkis como resolver questões que envolvem as funções e propriedades nas Operações Básicas com os Polinômios.
Gostou da aula com o Sarkis? O cara é mesmo fera!!!
Multiplicação de polinômio por polinômio
- Para efetuarmos a multiplicação de polinômio por polinômio, devemos utilizar a propriedade distributiva. Veja o exemplo:
- (x – 1) . (x2 + 2x – 6)
- x.x2 + x.2x – x.6 + (-1).x2 + (-1).2x – (-1).6
- x³ +2x² – 6x – x² – 2x + 6
 reduzindo os termos semelhantes.
reduzindo os termos semelhantes. - x³ + x² – 8x + 6
Divisão de polinômios![]()
Vamos dividir um polinômio por um monômio, com o intuito de entendermos o processo operatório. Observe:
Dica 1 – Tire todas as suas dúvidas sobre Funções Polinomiais de 2o grau em mais esta aula de revisão para a prova de Matemática Enem que preparamos para você – https://blogdoenem.com.br/funcao-polinomial-2o-grau-revisao-matematica-enem/
Funções e Propriedades nas questões de Polinônios
Exercícios resolvidos para você compreender como resolver os polinômios:
1. (UERJ, 2011)
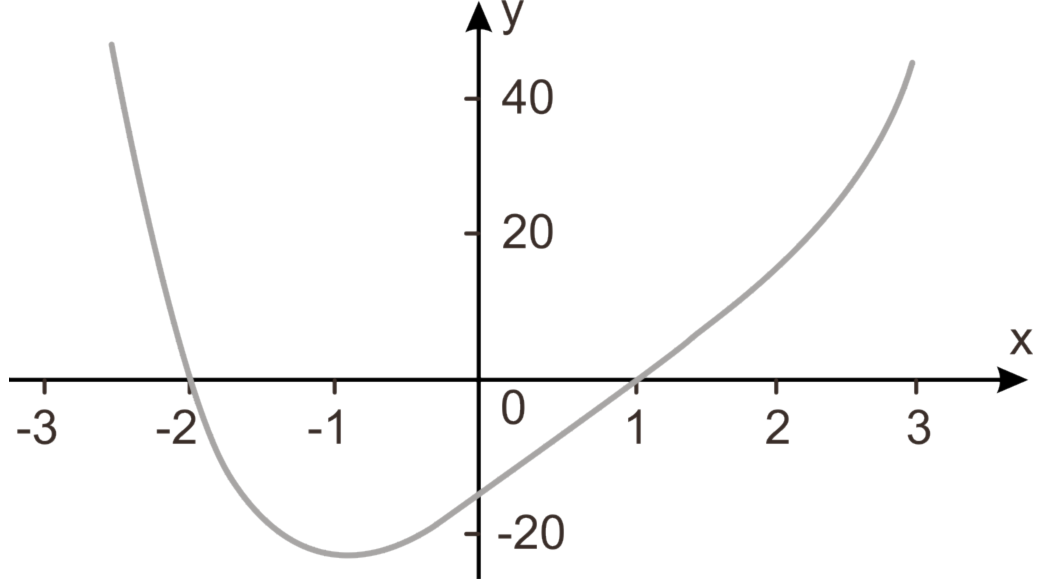
O gráfico acima representa uma função polinomial P de variável real, que possui duas raízes inteiras e é definida por: P(x)= x4 – 3x3 + 2x2 + 16x + m Agora, vamos ao problema: Determine o valor da constante representada por m: Como o gráfico intersecta o eixo dos x nos pontos de abscissa -2 e 1, segue que:
P(-2) = P(1) = 0 ⇔ 14 – 3 ⋅ 13 + 2 ⋅ 12 + 16 ⋅ 1 + m = 0 ⇔ m = -16
2. Seja S o conjunto solução da equação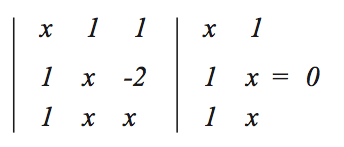
em R, então S está contido no intervalo [-2, 1].
Resolução:
Utilizando a regra de Sarrus, tem-se: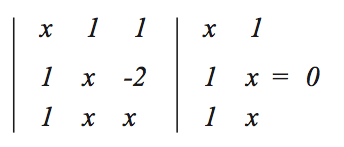
x3 – 2 + x – x + 2x2 – x = 0
x3 + 2x2 – x – 2 = 0
Nota-se que uma das raízes é x=1, pois
(1)3 +2 ⋅ (1)2 – (1) – 2 = 0.
Agora conhecendo uma das raízes, pode-se aplicar o dispositivo prático de Briot-Ruffine para encontrar as outras duas raízes.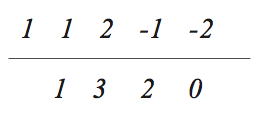
x2 + 3x + 2 = 0
x = -1 e x = -2
S = {-2;-1;1}
Considerando que {-2; -1; 1″} ⊂ [-2; 1], constata-se que o item é verdadeiro.
Exercícios sobre Funções e propriedades
Questão 1
(ENEM, 2a aplicação, 2010) Um laticínio possui dois reservatórios de leite. Cada reservatório é abastecido por uma torneira acoplada a um tanque resfriado. O volume, em litros, desses reservatórios depende da quantidade inicial de leite no reservatório e do tempo t, em horas, em que as duas torneiras ficam abertas. Os volumes são dados pelas funções:
V1(t) = 250t3 – 100t + 3000 e V2(t) = 150t3 – 69t + 3000
Depois de aberta cada torneira, o volume de leite de um reservatório é igual ao do outro no instante t = 0 e, também, no tempo t igual a
a) 1,3h
b) 1,69h
c) 10,0h
d)13,0h
e) 16,9h
Dica 1 – Revise os Paralelogramos nesta aula de Quadriláteros para a prova de Matemática Enem. Estude conosco para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/paralelogramos-matematica-enem/
Questão 2
(UEL, 2008) Considere a função polinomial f(x) = x3 + 2x + 3. Se h é um número real, assinale a alternativa que expressa corretamente o valor da função g definida por: g(h) = [f(3 + h) – f(3)]/h
a) g(h) = 29 + 9h + h2
b) g(h) = 2 + h2
c) g(h) = h2 +2-(18/h)
d) g(h) = h2 +2h-18
e) g(h) = h3 +2h+3
Dica 2 – Você sabe o que é um Trapézio? Se você ainda não o estudou, aproveite esta aula de Matemática Enem e saiba tudo sobre os Quadriláteros e suas definições – https://blogdoenem.com.br/quadrilateros-matematica-enem/
Questão 3 – Funções e Propriedades
(UEL, 2008) Seja g(x) = f(x + 1). Um esboço do gráfico da função f está ilustrado a seguir:
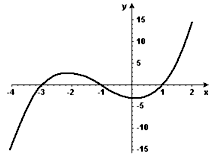
Considere as seguintes afirmativas:
I. A função g se anula em x = – 4, x = – 2 e x = 0.
II. Se – 4 ≤ x ≤ 0, então g(x) ≥ 0.
III. Se – 3 ≤ x ≤ – 2, então f(x) ⋅ g(x) ≥ 0.
IV. Existe x ∈ (0, 1), tal que g(f(x)) < 0.
Assinale a alternativa que contém todas as afirmativas corretas:
a) I e II
) I e III
c) II e IV
d) I, III e IV
e) II, III e IV
Dica 3 – Os Triângulos são semelhantes quando possuem dois ângulos internos iguais. Entenda tudo sobre a Semelhança entre triângulos nesta aula de Matemática Enem – https://blogdoenem.com.br/semelhanca-entre-triangulos-matematica-enem/
Questão 4
(UNIFESP, 2004) Se a figura representa o gráfico de um polinômio real, p(x), pode-se afirmar que:
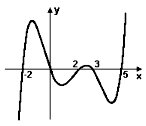
a) p(x) tem uma raiz a, tal que 3 < a < 5.
b) p(x) é divisível por x – 1.
c) p(x) tem apenas 4 raízes reais.
d) p(x) não tem raiz real.
e) o grau de p(x) é maior ou igual a 5.
Questão 5
Se a,b e c são as raízes da equação x3 – 7x + 6 = 0, então
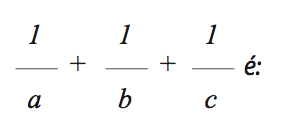
a) 7/6
b) 4
c) -6
d) 9/2
e) 3/5
Você consegue resolver estes exercícios sobre funções e Propriedades dos Polinômios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
 reduzindo os termos semelhantes.
reduzindo os termos semelhantes.
