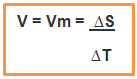Imagine você mantendo sua velocidade ou aceleração, de forma controlada. Sabia que você, é você mesmo, pode ser comparado às fórmulas matemáticas? Saiba mais sobre Movimento Uniformemente variado com este post de Física Enem e vestibular
Física Enem: Imagine duas situações: Se um objeto mantém velocidade constante, ele descreve um movimento uniforme. Se este mesmo objeto descreve um movimento com aceleração constante, teremos então um movimento uniformemente variado.
Você sabe a diferença entre os dois tipos de movimento? Vamos definir: Movimento uniforme é um movimento com velocidade constante, ou seja, o objeto percorre espaços(S) iguais em tempos(T) iguais.
Confira no resumo com o professor Antônio Martins, o Tonho do canal do Curso Enem Gratuito, como você difrencia o MU (Movimento Uniforme) do MRU (Movimento Retilíneo Uniforme), do MRUV (Movimento Retilíneo Uniformemente Variado), e do MUV – Movimento Uniformemente Variado.
Domine o Movimento Uniforme
Você pode ver com frequência o Movimento Uniforme. Por exemplo, em uma via sem engarrafamento. Neste exemplo, podemos ver a velocidade do carro constante durante um grande intervalo de tempo. Entenda as propriedades do Movimento Uniforme.

Propriedades do movimento uniforme
Se um objeto descreve um movimento uniforme, iremos observar duas propriedades muito importantes:
- – A primeira é que a aceleração deste objeto é nula (Vale recordar que para haver aceleração é necessário que exista variação de velocidade).
- – A segunda é que a velocidade constante coincide com a velocidade média, ou seja:

- Fórmula da Velocidade Média igual a Velocidade
Função Horária dos Espaços
Se um objeto descreve um movimento uniforme, as grandezas espaço e tempo sofrem variações.
Vamos imaginar a seguinte situação: Uma criança está em um carrinho de rolimã, com velocidade constante de 5 km/h.
A partir desta informação, estabelecemos um vínculo entre espaço e tempo: a cada uma hora a criança irá percorrer 5 km, e a cada 2 horas, ela percorre 10 km e assim sucessivamente.
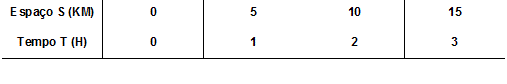
Veja o quadro:
Observando o quadro acima, veremos que a cada 1 hora, a criança percorre 5 km, e esta distância aumenta conforme o decorrer do tempo. Com a junção destes dados, podemos estabelecer uma fórmula matemática: Fórmula da Função Horária dos Espaços
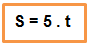
Veja que a relação de espaço e tempo vinculada para o movimento do carrinho se enquadra perfeitamente com os dados da tabela. Porém, vamos imaginar que a criança não tenha partido da origem do percurso, ou seja, do espaço zero, mas sim do ponto do trajeto 3 km.
Este fato não interfere a situação de que a criança vai percorrer 5 km em uma hora, mas depois de uma hora a posição dela não será no quilômetro 5, mas no quilômetro 8, e assim a tabela de Espaço(S) e Tempo(T) ficará deste jeito:
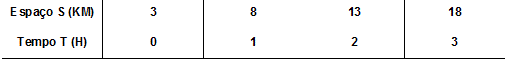
A fórmula matemática que relata o movimento também irá sofrer alteração, pois desta maneira teremos que somar 3 km à relação anterior, resultando:
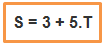
Veja a Fórmula da Função Horária dos Espaços alterada:
A partir desta nova fórmula, podemos comparar e verificar que o espaço inicial do carrinho (S0) é de 3 Km e que a velocidade (V) é de 5 km/h. Agora vamos transformar em uma fórmula mais geral:
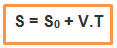
A fórmula matemática acima é chamada função horária dos espaços para o movimento uniforme.
Gráficos do Movimento Uniforme
O movimento de um objeto pode ser traduzido em fórmulas matemáticas, conforme demonstrado na Função Horária dos Espaços. Então, se conseguimos demonstrar um movimento através dessas fórmulas, é possível também representá-lo através de gráficos, que é uma maneira bastante eficiente de evidenciar a progressão dos resultados.
Veja agora com o professor de física Antônio Martins, o Tonho de Floripa, como resolver questões com Gráficos de Movimento Uniforme.
No movimento uniforme, os gráficos mais utilizados são: o de velocidade em função do tempo e o do espaço em função do tempo:
VELOCIDADE EM FUNÇÃO DO TEMPO
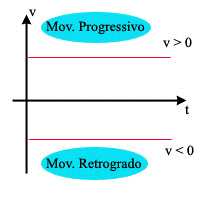
Observamos que o movimento uniforme tem como principal característica a velocidade constante. Portanto, a “cara” do gráfico será uma reta paralela ao eixo do tempo.
IMPORTANTE, caso a reta estiver acima do eixo do tempo, o movimento é chamado de progressivo. Porém se a reta estiver abaixo do eixo do tempo, o movimento é chamado de retrógrado. Veja o gráfico a seguir.
Gráfico da Velocidade em Função do Tempo no Movimento Uniforme
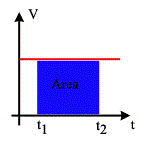
Aqui precisamos lembrar algo que pode te ajudar. Você sabia que para todo gráfico de velocidade em função do tempo, pode-se calcular a Variação de Espaço (∆S)? Sim, é que se calcularmos a área, que fica entre a curva do gráfico e o eixo do tempo (intervalo de tempo), essa área, será numericamente igual à trajetória do objeto.
Observe o gráfico a seguir: Gráfico da Velocidade em Função do Tempo para o cálculo da Área. Área = ∆S
ESPAÇO EM FUNÇÃO DO TEMPO
Anteriormente observamos que o espaço e tempo podem ser descritos por uma fórmula matemática:
S = S0 + V.T
Legenda: Fórmula Geral da Função Horária dos Espaços
Esta fórmula é uma Função do primeiro grau, ou seja, se buscarmos na matemática veremos que os resultados dessa função, colocados em gráficos, resultam em uma reta inclinada, como demonstrados abaixo:
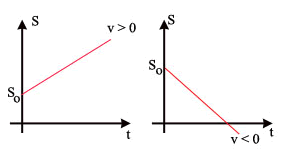
Analisando os gráficos, você vai verificar pontos importantes que caracterizam o Movimento Uniforme. O início da reta indica sempre o espaço inicial do objeto. Observe que se a reta tem inclinação para cima, à velocidade sempre é positiva e o movimento é progressivo.
Agora caso a reta tenha inclinação para baixo, a velocidade sempre é negativa e o movimento chamado de retrógrado. Veja o Resumo de Movimento Retilíneo Uniforme.
Gostou do resumo? Muito bom. Agora chegou a hoara de avançar para o resumo do MRUV, do Movimento Retilíneo Uniformemente Variado.
MRUV: Movimento Retilíneo Uniformemente Variado
Confira com o professor Antônio Martins, o Tonho, do canal do Curso Enem Gratuito.
A seguir coloquei alguns exercícios para você treinar sobre o assunto. Eles já possuem as respostas, mas eu desafio você.
Tente encontrar outras formas de resolver as questões, compare as duas, verifique as diferenças e post aqui no Blog. Tenho absoluta certeza de que você irá aprender muito mais assim.
Um abração e nos encontramos aqui no Blog do Enem.
EXERCÍCIOS sobre Movimento Uniformemente Variado
01- (ENEM-MEC) – Em uma prova de 100 m rasos, o desempenho típico de um corredor padrão é representado pelo gráfico a seguir:
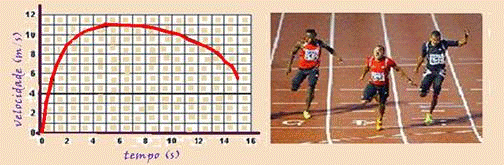
Em que intervalo de tempo o corredor apresenta aceleração máxima?
a) Entre 0 e 1 segundo.
b) Entre 1 e 5 segundos.
c) Entre 5 e 8 segundos.
d) Entre 8 e 11 segundos.
e) Entre 9 e 15 segundos.
02- (ENEM-MEC-09)
O Super-homem e as leis do movimento
Uma das razões para pensar sobre a física dos super-heróis é, acima de tudo, uma forma divertida de explorar muitos fenômenos físicos interessantes, dede fenômenos corriqueiros até eventos considerados fantásticos. A figura seguinte mostra o Super-homem lançando-se no espaço para chegar ao topo de um prédio de altura H. Seria possível admitir que com seus superpoderes ele estaria voando com propulsão própria, mas considere que ele tenha dado um forte salto.

Neste caso, sua velocidade final no ponto mais alto do salto deve ser zero, caso contrário, ele continuaria subindo. Sendo g a aceleração da gravidade, a relação entre a velocidade inicial do Super-homem e a altura atingida é dada por:
v2 = 2gh.
A altura que o Super-homem alcança em seu salto depende do quadrado de sua velocidade inicial por que:
(A) a altura do seu pulo é proporcional à sua velocidade média multiplicada pelo tempo que ele permanece no ar ao quadrado.
(B) o tempo que ele permanece no ar é diretamente proporcional à aceleração da gravidade e essa é diretamente proporcional à velocidade.
(C) o tempo que ele permanece no ar é inversamente proporcional à aceleração da gravidade e essa é inversamente proporcional à velocidade média.
(D) a aceleração do movimento deve ser elevada ao quadrado, pois existem duas acelerações envolvidas: a aceleração da gravidade e a aceleração do salto.
(E) a altura do pulo é proporcional à sua velocidade média multiplicada pelo tempo que ele permanece no ar, e esse tempo também depende da sua velocidade inicial.
03- (UFPR-PR) Em uma prova internacional de ciclismo, dois dos ciclistas, um francês e, separado por uma distância de 15 m à sua frente, um inglês, se movimentam com velocidades iguais e constantes de módulo 22 m/s. Considere agora que o representante brasileiro na prova, ao ultrapassar o ciclista francês, possui uma velocidade constante de módulo 24 m/s e inicia uma aceleração constante de módulo 0,4 m/s2, com o objetivo de ultrapassar o ciclista inglês e ganhar a prova.

No instante em que ele ultrapassa o ciclista francês, faltam ainda 200 m para a linha de chegada. Com base nesses dados e admitindo que o ciclista inglês, ao ser ultrapassado pelo brasileiro, mantenha constantes as características do seu movimento, assinale a alternativa correta para o tempo gasto pelo ciclista brasileiro para ultrapassar o ciclista inglês e ganhar a corrida.
a) 1s.
b) 2s.
c) 3s.
d) 4s.
e) 5s.
04- (UFES-ES) Um predador, partindo do repouso, alcança sua velocidade máxima de 54 km/h em 4 s e mantém essa velocidade durante 10 s. Se não alcançar sua presa nesses 14 s, o predador desiste da caçada. A presa, partindo do repouso, alcança sua velocidade máxima, que é 4/5 da velocidade máxima do predador, em 5 s e consegue mantê-la por mais tempo que o predador.

Suponha-se que as acelerações são constantes, que o início do ataque e da fuga são simultâneos e que predador e presa partem do repouso. Para o predador obter sucesso em sua caçada, a distância inicial máxima entre ele e a presa é de:
a) 21 m
b) 30 m
c) 42 m
d) 72 m
e) 80 m
GABARITO
1 – A 2 – E 3 – E 4 – C
Tem dúvida ainda sobre o movimento uniformemente variado? Veja um novo resumo do curso enem gratuito