Na aula de hoje tire suas dúvidas sobre a função Seno. Entenda como as relações Trigonométricas se estabelecem, e domine os fundamentos que começam com os Triângulos e o Teorema de Pitágoras. Vem, para ficar afiado e gabaritar na prova de Matemática do Enem
Esta aula apresenta a função seno. Desta função, serão estudados o seu conceito, o seu domínio (intervalos de existência da função), sua imagem, a variação do sinal da função no ciclo trigonométrico, seu gráfico e algumas propriedades.
Venha fazer parte desta aula e dê um show em Matemática no Enem! Pois bem, o básico do básico na Trigonometria começa com o Teorema de Pitágoras.
Se você já domina que a soma do quadrado dos catetos é igual ao quadrado da hipotenusa, é hora de mergulhar mais fundo e aprender (ou lembrar) Seno e Cosseno.
Vamos considerar o triângulo da figura abaixo: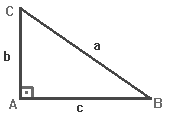
Em um triângulo retângulo, temos dois lados que formam ângulos com a hipotenusa, então para não criar confusões, denomina-se o lado sempre tomando como referência o ângulo ao qual ele está relacionado.
Para isso, acompanhe a tabela abaixo:
O lado adjacente, que citei na tabela acima, é o lado que descreve o ângulo junto com a hipotenusa.
Agora, treine com os exercícios abaixo a aplicação do teorema de Pitágoras, procure destacar em cada um dos exercícios resolvidos qual é o nome de cada lado (se é oposto ou adjacente) em relação aos ângulos da figura.
Então, já que você entendeu o processo acima, vamos trabalhar a ideia principal desse nosso post. Para isso, vamos contextualizar um pouco a motivação deste estudo.
Veja uma aula gratuita com o professor Sarkis, com exercícios resolvidos, e logo vamos continuar.
.
Processo histórico da Trigonometria
A essa altura, você já deve saber que a Matemática sempre andou de mãos dadas com a Astronomia, Agrimensura e as Navegações. E, por conta dessa proximidade, muitos dos problemas que surgiram com essas ciências utilizaram recursos da Álgebra e Geometria para encontrar suas respectivas soluções.
Por exemplo, no ENEM de 2009, caiu uma questão interessante que envolvia três irmãos que dividiriam uma herança com uma área de extração de ouro delimitada por uma região circular.
Se tomarmos emprestado uma parte desse problema, teríamos a seguinte figura geométrica: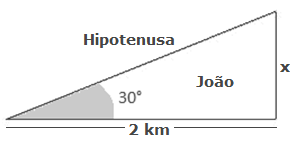
E, para encontrar o valor do lado X deste triângulo usaremos as relações trigonométricas, pois com elas podemos associar as razões entre dois lados (oposto e adjacente) a uma medida específica de cada ângulo.
No nosso caso, podemos fazer três associações:
|
Ângulo |
1ª Razão |
2ª Razão |
3ª Razão |
|
30° |
x/hipotenusa |
2/hipotenusa |
x/2 |
Para a 1ª razão, damos o nome de SENO. Já para a 2ª razão, damos o nome de COSSENO e para a 3ª razão, damos o nome de TANGENTE. Agora, você deve estar se perguntando: porque esses nomes?
Primeiro, a história da matemática possui alguns fatos interessantes. Por volta de 500 d.C. os hindus chamavam o nosso atual SENO de JIVA. Que ao ser traduzido pelos árabes (que tinham o costume de escrever somente as consoantes) ficou conhecido como JAIB, ao invés de JIBA (denominação correta segundo o conceito hindu).
E, este quando foi traduzido para o latim, chegou até nós como SINUS. Se quiser saber mais sobre este processo histórico e a origem dos outros nomes fica a dica abaixo.
Dicas de Trigonometria:
Respondendo a sua provável segunda inquietação, é muito simples guardar qual razão está relacionada com qual lado, veja:
Existe até uma brincadeira que fazemos em sala de aula para vocês guardarem essas siglas, imagine que eu estou parado em frente à escola em que vou aplicar a prova do ENEM.
Ao olhar no relógio, vejo que estou atrasado, então, pego a minha coca e saio correndo, no caminho tomo um tombo daqueles e chego todo molhado na sala de aula, para justificar a vocês digo:
“CORRI e CAÍ com COCA!” à (Cohi, Cahi, Coca).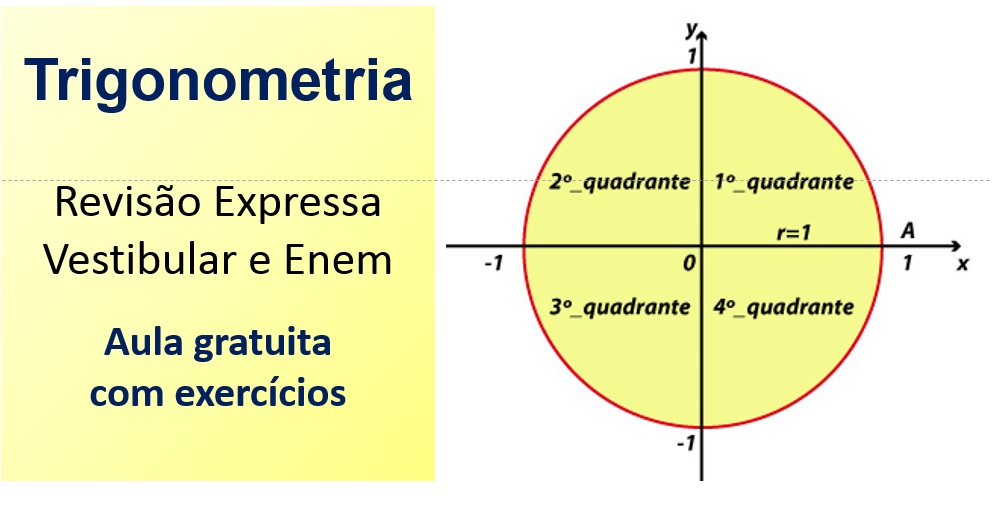
Dica do Blog: Conheça mais sobre o processo histórico e enriqueça suas ideias trigonométricas em https://ecalculo.if.usp.br/historia/historia_trigonometria.htm
E, veja também uma aula completa sobre o Círculo Trigonométrico one você aprende a utilizar os eixos X e Y, e os Quatro Quadrantes do Círculo para fazer os cálculos necessários.
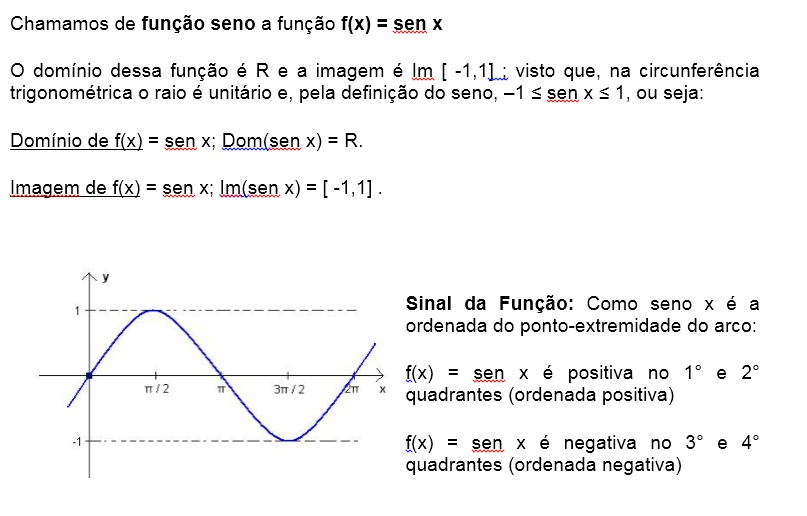
Veja agora nos quadrantes do Círculo Trigonométrico:
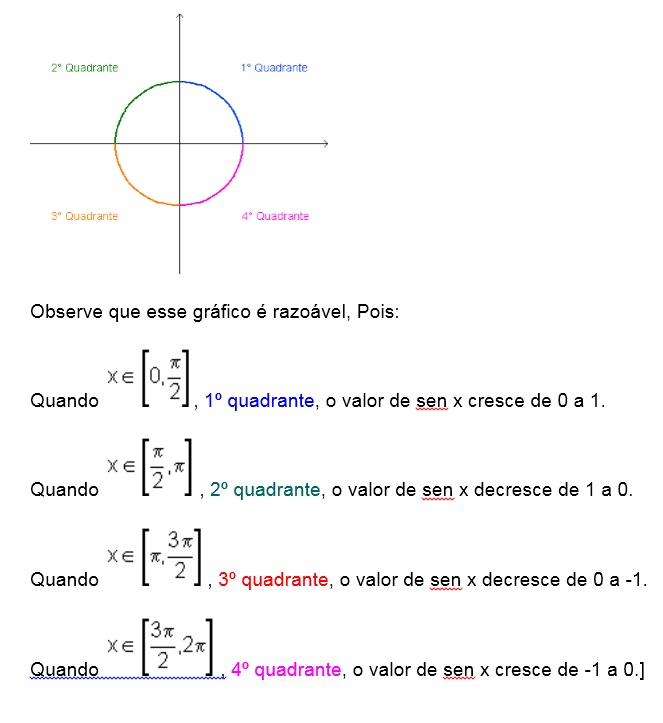
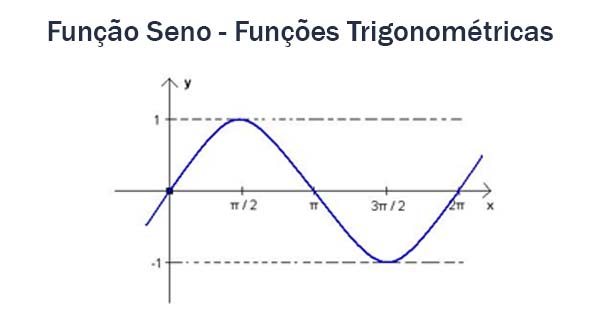
Variação da função seno
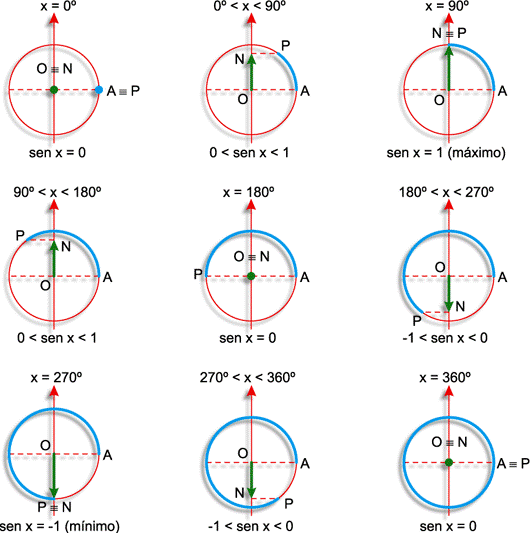
Gráfico
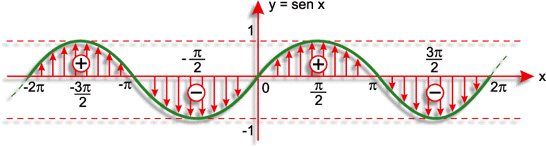
E aí, vamos assistir a essa vídeoaula que traz o gráfico da função seno de forma descomplicada. Não esqueça de resolver os exercícios. Boa sorte!
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.
