Agora, toda vez que você olhar para um prédio e imaginar a altura dele vai saber que precisa aplicar o Teorema de Teles. O cálculo sempre aparece na prova de Matemática do Enem
Muitas vezes, o aluno quer aprender de cara a resolver as questões de matemática sem antes entender o conceito por trás de cada fórmula. Conhecer a lógica de pensamento do autor, ajuda no processo de aprendizagem.
Se você apreender os conceitos e não apenas decorar as fórmulas, vai perceber como essa matéria, temida por tantos alunos, pode ficar bem fácil. Com o Teorema de Tales não é diferente.
Dica 1: domine as operações de cálculo de juros: https://blogdoenem.com.br/
Quem foi Tales de Mileto
Tales de Mileto foi um filósofo grego, que viveu por volta de 623 a.C onde hoje é o território da Turquia. Ele foi responsável por diversas descobertas na área das exatas. Foi Tales quem demonstrou importantes relações entre triângulos, circunferências e ângulos que até hoje são referências nos cálculos matemáticos.
Mas o trabalho pelo qual ele foi mais reconhecido foi o famoso Teorema de Tales. Mas antes de estudá-lo, é importante entender a diferença entre teorema e teoria.
Dica 2: está perdido com tanto conteúdo? Saiba o que revisar para a prova de Matemática do Enem:https://blogdoenem.com.br/
Teoria x Teorema
Toda vez que você deparar com a palavra “teoria” quer dizer que está diante de um conjunto de princípios. Toda teoria apresenta uma noção geral sobre determinado assunto e, portanto, passa uma ideia bastante abrangente sobre o tema.
A teoria, portanto, apresenta uma hipótese, uma conjectura e até mesmo uma opinião sobre um contexto. Diferentemente de outras disciplinas, em matemática toda teoria precisa demonstrada. Assim, uma teoria precisa ser discutida e, com o tempo, revista.
Um exemplo bastante conhecido é a Teoria da Relatividade. Apesar de todos os indícios, ainda não é possível comprová-la através de experimentos. Para isso, seria preciso enviar astronautas para o espaço na velocidade da luz.
Por outro lado, o teorema pode ser demonstrado matematicamente. De forma resumida, um teorema pode ser comprovado, enquanto a teoria não. Isso significa que é possível comprovar a veracidade do Teorema de Tales através dos números.
Dica 3: o que mais cai em Matemática nos Vestibulares e no Enem? Veja aqui as melhores dicas: http://blogdoenem.com.
Teorema de Tales
O professor Luis Carlos Rodrigues da Costa apresenta uma explicação bem interessante sobre esse assunto tão cobrado nas provas de matemática do Enem. A videoaula tem 5min39 e está disponível no canal aberto do Youtube. Dá uma olhada:
Dica 4: a Regra de Três composta ainda é um problema sem solução pra você? Tire todas as dúvidas aqui https://blogdoenem.com.br/
Teorema de Tales na prova de Matemática do Enem
Tales aplicou conceitos da Geometria para determinar a altura de uma pirâmide. A ferramenta utilizada para o cálculo é a proporcionalidade. Ele observou que os raios solares chegavam inclinados e paralelos em relação à Terra.
A partir dessa percepção, criou o conceito de proporcionalidade entre as medidas da sombra e a altura dos objetos. É a ideia de proporção aplicada à Geometria Plana. Objetos distantes e com uma escala muito grande, a partir dessa teoria já podiam ser medidos.
O Teorema de Tales pode ser determinado pela seguinte lei de correspondência: “feixes de retas paralelas cortadas ou intersectadas por segmentos transversais formam segmentos de retas proporcionalmente correspondentes”.
Para compreender melhor, observe o esquema representativo:
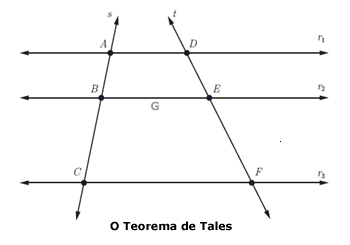
Logo:
AB = D’E’
BC E’F’
A questão abaixo foi aplicada à prova do ENEM de 2009:
A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é:
a) 1,16 metros. d) 5,6 metros. b) 3,0 metros. e) 7,04 metros. c) 5,4 metros.
Para resolver essa questão, utilizaremos o Teorema de Tales, logo:
x é o comprimento que o paciente ainda deve caminhar.
Assim:
2,2 = 0,8 → x + 3,2 = 8,8 → x =5,6
X+3,2 3,2
Gabarito: d
Vamos ver mais uns exercícios de para fixar a matéria?
1) Calcule o valor de “x” e “y”, sabendo que a//b//c//d:
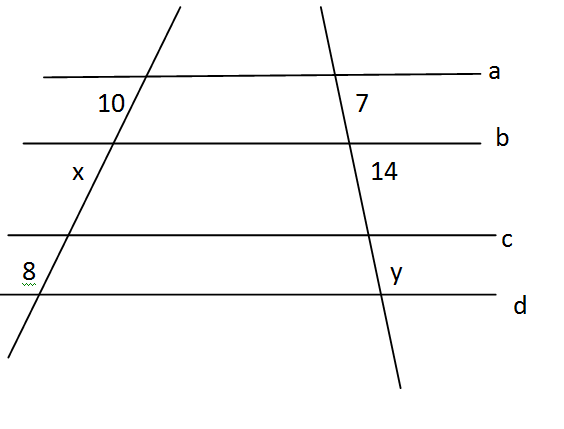
10/x = 7/14
Logo: 7x = 140, então: x = 20
Agora, podemos calcular o valor de y:
20/8 = 14/y
Logo: 20y = 112, então: y = 5,6
Assim: x= 20 e y = 5,6
2) Calcule o valor de DE//BC do triângulo:
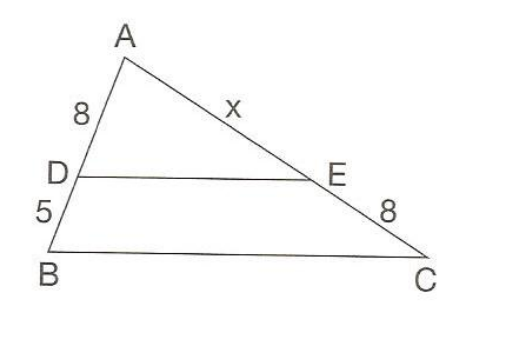
8/5 = x/8
Logo: 5x = 64, então: x = 12,8
Como você pode observar não é tão difícil!
Este texto foi produzido por Leonardo Ferreira. Ele atuou como professor de Matemática em projetos sociais. Em sua trajetória, foi aprovado em Matemática-UERJ e Ciências Contábeis-UFF, mas optou pela bolsa integral do PROUNI para o curso de Ciência Contábeis da Cândido Mendes através do ENEM. Pretende cursar o mestrado para se dedicar a uma das suas maiores paixões: dar aulas. https://www.facebook.
