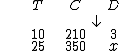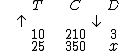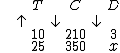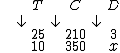Veja aula gratuita e demonstração com exercício resolvido de um conteúdo elementar de Matemática Enem: Razão e Proporção. Entenda as relações 'diretamente proporcionais' e 'inversamente proporcionais'. É o básico do básico, mas ajuda você em diversas áreas da prova do Enem e do Vestibular também. Confira abaixo.
O assunto de hoje trata de Razão e Proporção. Mas, o que são ‘proporções’? Um exemplo bem prático de Matemática Enem no qual enxergamos certa proporção é ao fazer um pouco de café. Acompanhe no exemplo abaixo.
Normalmente, nos rótulos dos pacotes de café, está especificado na receita. A medida recomendada é esta: 4 colheres para 1 litro de água. Identificamos aqui duas grandezas proporcionais: uma delas é quantidade de pó de café (quatro colheres), e a outra é a quantidade de água (um litro). Facilmente se percebe que quanto mais litros de café você quer fazer, mais colheres de pó terá que usar. Assim, dizemos que as grandezas “pó” e “água” são diretamente proporcionais, pois a medida que uma quantidade aumenta o mesmo ocorre com a outra.
Vejamos um exemplo de duas grandezas inversamente proporcionais: – Supomos que dois pedreiros construam uma casa em 30 dias. Mas, ao aumentar a quantidade de pedreiros trabalhando na mesma empreitada, a relação com o tempo necessário para construir a mesa casa muda. Perceba, então, que se o número de pedreiros aumentar, a casa será construída em menos dias. Portanto, dizemos que as grandezas “quantidade de pedreiros” e “dias de construção” são inversamente proporcionais. Ou seja, se ‘aumenta’ a quantidade de pedreiros, ‘diminuem’ os dias da construção.
Diferença entre ‘diretamente proporcional’ e ‘inversamente proporcional’
Por outro lado, se a proposição fosse assim, tudo seria diferente na relação: supomos que dois pedreiros construam uma casa de 40 metros quadrados em 30 dias. Porém, se a metragem da construção for alterada para 60 metros quadrados, em quanto tempo os dois pedreiros construiriam a casa? Você já percebeu que o tempo vai aumentar, claro. Portanto, dizemos neste caso que as grandezas ”quantidade de metros quadrados’ e ‘dias de construção’ são diretamente proporcionais. Ou seja, se ‘aumenta’ uma, a outra ‘aumenta’ também.
Viu como não há segredo para trabalhar com o que é ‘diretamente proporcional’ e com o que é ‘inversamente proporcional’? Conhecer esta lógica ajuda você em diversas matérias das provas do Enem e do Vestibular.
Aula gratuita de Razão e Proporção para resolver Regra de Três
Acompanhe uma super aula do professor Sérgio Sarkis sobre como resolver regras de três simples e compostas. Após essa aula, tente resolver os exercícios abaixo.
Agora que já viu essa aula videoaula bacana, tente resolver os exercícios abaixo.
EXERCÍCIOS
1) Um tecelão levou 12 horas para produzir um tapete, à razão de 6 metros por hora. Se ele trabalhasse à razão de 9m/h, quanto tempo teria levado para tecer o mesmo tapete?
2) 2) Um grupo de 10 trabalhadores descarregam 210 caixas de mercadoria em 3 horas. Quantas horas 25 trabalhadores precisarão para descarregar 350 caixas?
RESPOSTAS
1) Temos a grandeza tempo (T) e a grandeza velocidade de produção (V). Quando a velocidade aumenta, o tempo diminui visto que estamos produzindo uma metragem maior, notamos então que as duas grandezas são inversamente proporcionais e na representação, as duas terão a seta com orientação invertida e será necessário que se faça a inversão de termos para torná-las diretamente proporcionais:
Procedendo com a inversão temos:
Basta resolvermos então a questão:
À razão de 9m/h, o tecelão teria levado 8 horas para tecer o tapete.
2) Primeiro passo, atribuir uma letra a cada uma das grandezas:
• T: O número de trabalhadores;
• C: A quantidade de caixas;
• D: A duração da operação de descarga.
Do enunciado temos a seguinte representação para a análise do problema:
A grandeza procurada (D) está à esquerda para que seja isolada mais facilmente no último passo. Como já padronizamos, arbitremos que a orientação da grandeza D seja para baixo:
As grandezas D e T terão as setas com orientação oposta, isto porque ao aumentarmos o número de trabalhadores, diminuiremos o tempo da operação de descarga (considerando-se apenas as duas grandezas):
Se aumentarmos a quantidade de caixas a descarregar, também aumentaremos a duração da operação, sendo assim as grandezas D e C são diretamente proporcionais, e terão a mesma orientação de seta:
Como a grandeza T tem orientação oposta, iremos realizar a sua inversão:
Finalmente, montaremos a proporção e iremos resolvê-la:
Conclusão: 350 caixas podem ser descarregadas por 25 trabalhadores em 2 horas de trabalho.
