Aprenda o que são números complexos, sua forma algébrica e como fazer operações com eles neste resumo de Matemática!
Os números complexos são úteis para resolver equações do tipo x² + 1 = 0, uma vez que não existe qualquer número real com a propriedade que seu quadrado seja igual a -1.
O que são números complexos
Os números complexos são números compostos por uma parte real e uma parte imaginária.
Na Matemática, eles surgiram para suprir a necessidade de resolver equações que envolviam a raiz quadrada de números negativos, o que não era possível trabalhando apenas com os números reais.
A solução desse problema foi sugerida pelo matemático italiano Rafael Bombelli. Denominou-se √–1 como unidade imaginária e foi criado o número i, de modo que:
i = √–1
i² = -1
Assim, foi criado o conjunto dos números complexos, representado por C.
Definição de número complexo
O número complexo pode ser definido como um número composto por uma parte real e uma parte imaginária. Todo número complexo z pode ser escrito na forma algébrica, da seguinte maneira:
z = a + bi, com a, b ∈ ℝ e i² = -1.
Além da forma algébrica, eles também podem ser expressos na forma trigonométrica.
Parte real e parte imaginária
Como já vimos, o número complexo possui uma parte real e uma parte imaginária. Isso pode ser facilmente observado quando analisamos a sua forma algébrica:
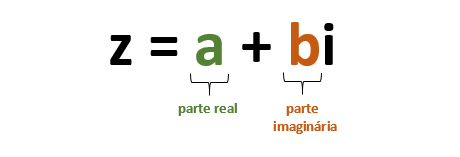
Dado o número complexo z = a + bi, então a é a parte real de z, denotada por Re(z) e b é a parte imaginária de z, denotada por Im(z). Em resumo:
- a e b são números reais
- a é a parte real, denotada por Re(z)
- b é a parte imaginária, denotada por Im(z)
- i é a unidade imaginária
Número imaginário puro
Quando a parte real de um número complexo é nula, ele é considerado um número imaginário puro. Ou seja, na expressão z = a + bi temos que a = 0. Assim, um número imaginário puro ser representado por z = bi.
Exemplos
- z = 3 + 0i é um número real, pois Re(z) = 3 e Im(z) = 0
- z = 7 + 4i é um número complexo, pois Re(z) = 7 e Im(z) = 4
- z = 0 + 5i é um número imaginário puro, pois Re(z) = 0 e Im(z) = -5
- z = -2 + 0i é um número real, pois Re(z) = -2 e Im(z) = 0
- z = 0 + 0i é um número real, pois Re(z) = 0 e Im(z) = 0
Operações com números complexos
Se os números complexos surgiram para possibilitar a resolução de equações, nada mais lógico que a possibilidade de realizar operações com eles, não é?
Adição de números complexos
Para fazer a adição, fazemos a adição dos termos semelhantes. Ou seja, somamos as partes reais e depois as partes imaginárias de cada número.
Por exemplo, vamos trabalhar com os números complexos z1 = a + bi e z2 = c + di. A adição dos números complexos z1 e z2 vai acontecer da seguinte forma:
z1 + z2 = (a + bi) + (c + di)
Por fim, vamos somar as partes reais com as partes reais e as partes imaginárias com as partes imaginárias:
z1 + z2 = (a + c) + (b + d)i
Subtração de números complexos
A subtração é feita seguindo a mesma lógica da adição, ou seja, com a subtração dos termos semelhantes. Assim, subtraem-se as partes reais e depois as partes imaginárias de cada número.
A subtração de números complexos pode ser expressa da seguinte maneira:
z1 – z2 = (a – c) + (b – d)i
Multiplicação de números complexos
A multiplicação é feita multiplicando cada termo do primeiro fator por todos os membros do segundo fator. Vamos novamente demonstrar com os números z1 = a + bi e z2 = c + di. A multiplicação de z1 e z2 será feita da seguinte maneira:
z1 . z2 = (a + bi) . (c + di)
Aplicando a propriedade distributiva da multiplicação, temos que:
z1 . z2 = (ac – bd) + (ad + bc)i
Divisão de números complexos
Para aprender a dividir números complexos, é necessário entender o que é o conjugado de um número complexo.
O conjugado é encontrado trocando o sinal da parte imaginária. Assim, o conjugado de z = a + bi será z = a – bi. Como regra, sempre que fizermos a multiplicação de um número complexo pelo seu conjugado, o denominador será um número real.
A divisão de números complexos é realizada multiplicando o numerador e o denominador pelo conjugado do denominador. Mais uma vez, vamos trabalhar com os números z1 = a + bi e z2 = c + di.
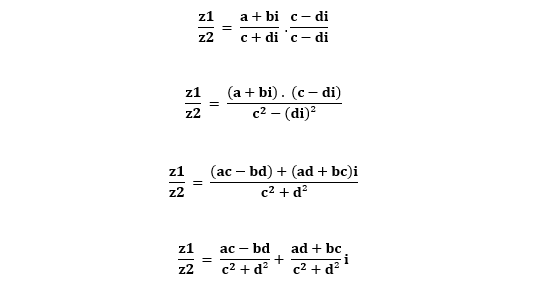
Videoaula
Assista à videoaula abaixo e tire suas dúvidas sobre o assunto!
Exercícios sobre números complexos
Resolva os exercícios abaixo e teste seus conhecimentos!
Números Complexos
-
Pergunta 1 de 10
1. Pergunta
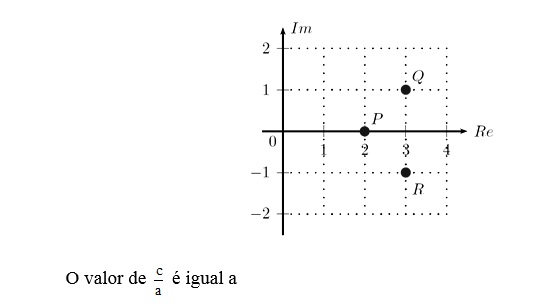
(UEFS BA/2016)
Os números complexos z e w têm módulos |z|=|w|=1 ;….
Se z, w e seu produto zw formam, no plano de Argand-Gauss, os vértices de um triângulo equilátero, é correto afirmar que