Tire suas principais dúvidas sobre As Medidas de Dispersão essenciais no domínio da matemática estatística: Amplitude, Variância, e Desvio Padrão. Aula com resumo, dicas e exercícios
As medidas de dispersão medem a variabilidade dos dados em estudo, como por exemplo, a amplitude, a variância, o desvio padrão e o coeficiente de variação. Elas permitem verificar se o conjunto de dados é homogêneo ou heterogêneo. Venha conferir esta aula para garantir sua prova de matemática no Enem!!!
MEDIDAS DE DISPERSÃO (Medidas de variabilidade)
Quando usamos uma “medida de tendência central” como a média, a mediana ou a moda, para caracterizar uma amostra, esquecemos de dizer se existe muita variabilidade dos indivíduos, ou não. 
Por exemplo, saber que o rendimento per capita médio dos EUA (31338$ de 95 em 2000) é igual ao rendimento per capita médio da Islândia (31342$ de 95 em 2000), não nos permite saber se existe uma maior percentagem de pessoas carentes nos EUA do que na Islândia.
Resumo gratuito: Como calcular Medidas de Dispersão
Gostou do resumo? O prof. Lucas é do canal do Curso Enem Gratuito. Têm mais aulas dele lá com diversos temas da matemática que são super importantes na sua preparação para o Exame Nacional do Ensino Médio.
Dica para Medidas de Dispersão: No sentido de caracterizar a heterogeneidade da amostra temos que acrescentar à medida de tendência central, uma medida de dispersão, enriquecendo-se assim a descrição da população.
Amplitude
Amplitude total ou máxima é a diferença entre o maior e o menor valor de um conjunto de dados. Como, por exemplo, nas médias das notas do teste psicotécnico da Tabela 1 em que a amplitude máxima é dada pela diferença entre 75 e 60, ou seja, 05. Logo, as notas do teste variam em 5 unidades.
Mas, para estudar a dispersão dos dados, a amplitude não é um dos melhores meios, pois o cálculo é efetuado apenas com os valores extremos do conjunto. Por exemplo, as idades em anos de um grupo de pessoas, são: 2, 5, 8, 10, 14, 18 e 22.
Um segundo grupo, possui as idades:2, 14, 15, 15, 16,16 e 22.
Nos dois grupos a amplitude máxima é de 20 anos. Porém, a dispersão no primeiro é bem maior do que no segundo. Para medir a dispersão de um grupo de dados, o pesquisador poderá fazer uso do desvio padrão: um procedimento matemático igualmente fácil, mas muito mais elaborado e que contempla todos os valores do conjunto de dados em estudo.
Variância
A variância da amostra é aproximadamente a média das diferenças ao quadrado entre cada uma das observações de um conjunto de dados. Assim, para uma amostra contendo n observações x1, x2, …, xn, a variância da amostra pode ser escrita como
Dica 1: Você ainda lembra a diferença entre a média aritmética e a média ponderada? Não, então clique aqui e tire mais essa dúvida. Continue sua rotina de estudos para arrasar na Matemática do Enem.
Desvio Padrão
O desvio padrão de uma amostra (representado pela letra S) é definido como sendo a raiz quadrada da variância da amostra.
Ao iniciar as análises de um agrupamento de dados, a média permite que se estabeleça um juízo sobre tal conjunto. Porém, não permite avaliar a dispersão, principalmente para conjunto de dados mais numerosos.
Um dos modos mais simples de se medir a dispersão, é calcular a amplitude total, entretanto, tal amplitude pode se deixar influenciar pelos valores extremos. O desvio padrão foge a essa falha por levar em conta todos os valores em questão. Portanto, o desvio padrão é muito mais conveniente no cálculo da dispersão.
O desvio padrão é definido como a raiz quadrada da média dos quadrados dos desvios (variância):
Desvio padrão populacional
O desvio padrão populacional ou amostral mede a variabilidade dos dados, com respeito à média. Conjunto de dados com maior dispersão implica em desvios padrões elevados.
A diferença entre o desvio padrão populacional e o desvio padrão amostral, está no significado do conjunto e no denominador da expressão matemática que o determina. Enquanto o desvio padrão amostral é calculado com a média de uma amostra da população. Portanto, expresso a partir de um valor estimado da verdadeira média.
O desvio padrão populacional é obtido com a média verdadeira, ou seja, a média da população. Então, o denominador n do desvio estimado, é subtraído de uma unidade como forma de correção, uma vez que essa subtração implica em um aumento de seu valor e, portanto, o uso do desvio padrão amostral tem diminuído a possibilidade de erro quando for usado para verificar a variabilidade dos dados.
Para exemplificar a análise de variabilidade de dados, analisar-se-á 4 amostras de massas de alunos iniciantes em um curso de graduação. Os dados com as estaturas destes alunos, constam abaixo.
Amostras com massas de alunos de graduação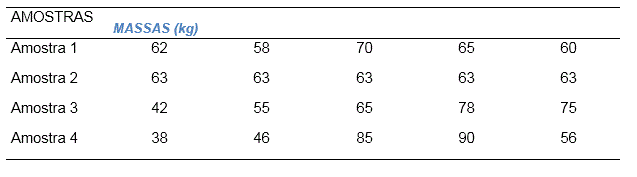
Em ambas as amostras da tabela acima, a média das massas dos alunos é 63 kg. Entretanto, a dispersão observada não é a mesma.
Para a amostra 1, o desvio padrão amostral é de 4,69 kg, a segunda amostra não possui variabilidade, na terceira o desvio padrão é de 14,82 e, para a quarta, este valor sobe para 23,32. Comparando os resultados dos desvios padrões calculados, se observa que, quanto maior for a dispersão dos dados, maior será o valor numérico do desvio padrão. Ressalta-se que o desvio padrão somente tem sentido enquanto informação se for comparado com a média.
O que a Variância e o desvio padrão indicam?
A variância e o desvio padrão medem a dispersão “média” em torno da média aritmética, ou seja, como as observações maiores flutuam acima dela e as observações menores se distribuem abaixo dela.
Dica 2: E como anda seus conhecimentos em Funções? Da Exponencial você lembra direitinho? Não, então clique aqui e revise esta aula para mandar muito bem na prova de matemática do Enem!
Coeficiente de variação
O coeficiente de variação dá uma ideia da precisão de um experimento ou da dispersão de um conjunto de dados. É definido como o quociente entre desvio padrão e a média, multiplicado por 100. Logo, o coeficiente de variação nada mais é do que o desvio padrão em porcentagem da média.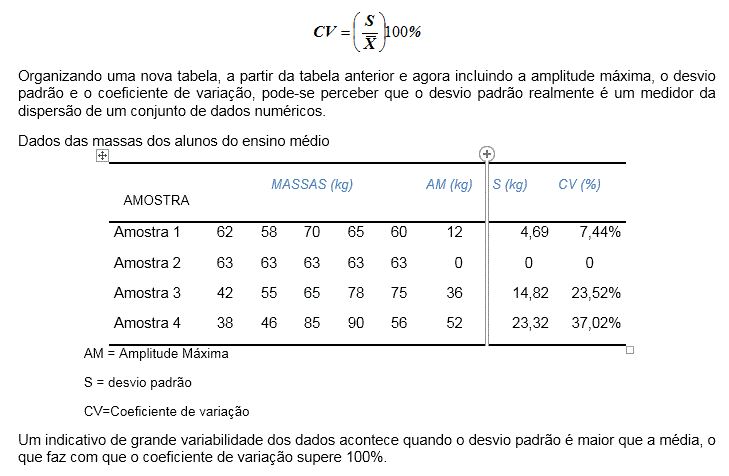
.
.
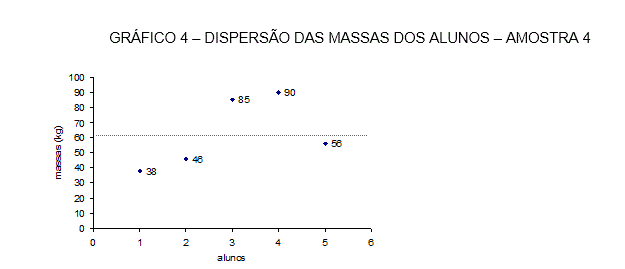
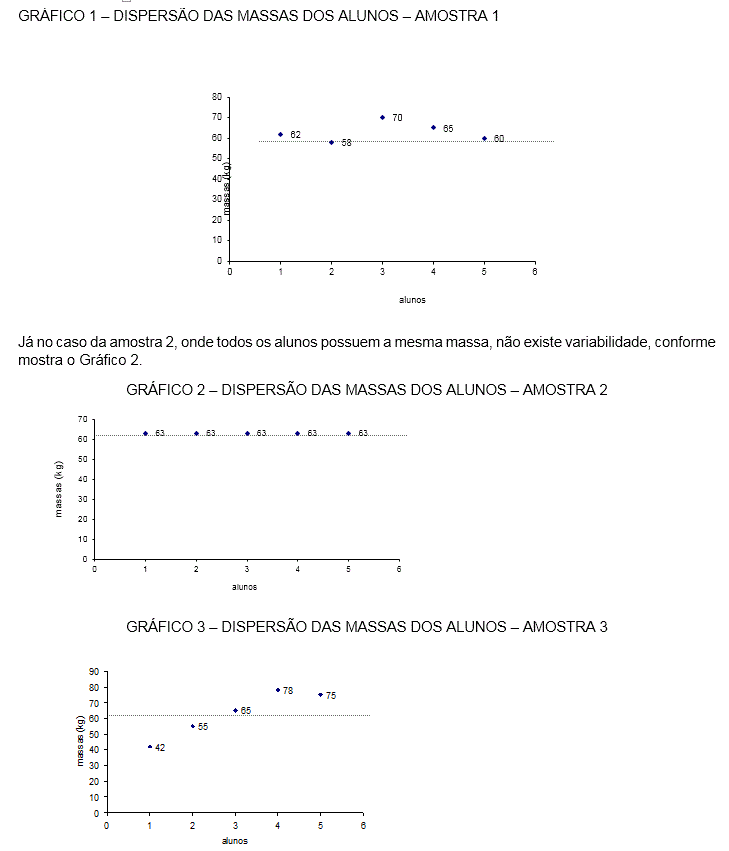
Os gráficos 1, 2, 3 e 4 indicam a variabilidade dos dados subjetivamente. Entretanto, o gráfico 4 é o que possui maior distanciamento dos dados da amostra, com respeito à média, simbolizada por uma linha pontilhada horizontal.
E aí, está entendo tudo sobre Medidas de dispersão? Se ainda ficou alguma dúvida, confira a aula abaixo para ampliar seus estudos. Até a próxima.
Gostou do vídeo? Agora é hora de enfrentar os desafios parar ver se você aprendeu mesmo a fazer os cálculos das Medidas de Dispersão.
Exercícios sobre Medidas de Dispersão
