Que tal centralizar seus estudos nesta aula sobre medidas de Tendências Centrais? Serão apresentadas duas medidas de posição: Moda e Mediana. Participe deste estudo e fique preparado para a matemática do Enem!
As medidas de tendência central são valores que, de certa forma, e de maneira condensada, trazem consigo informações contidas nos dados estatísticos – sejam eles, populacionais ou amostrais. Elas funcionam como uma espécie de “medidas-resumo”, pois nos passam a ideia, digamos, do comportamento geral das observações estudadas. Aprenda conosco os conceitos de Média, Moda e Mediana!
Podemos dizer ainda que elas são como valores de referência, em torno dos quais, os outros se distribuem. Quando estão associadas aos dados populacionais, são chamadas de parâmetros; quando são calculadas a partir de amostras, são denominadas estatísticas.
Essa diferença ocorre porque os parâmetros são valores constantes (fixos), pois são calculados a partir de todos os dados de certo conjunto, isto é, a população de interesse. Porém, se trabalhamos com amostras, as medidas estatísticas obtidas variarão de acordo com as observações que foram selecionadas.
Por isso, elas não são valores fixos, pois dependem dos elementos da amostra particular que foi escolhida. Veremos, agora, os conceitos e os cálculos de cada uma delas. Moda e Mediana: conceitos e cálculos.
Mediana
Considere a seguinte situação:
Os salários de 5 pessoas que trabalham em uma empresa são: $700,00 ; $800,00 ; $900,00 ; $1.000,00 e $5.600,00. O salário médio dessas 5 pessoas é:
![]()
Parece lógico que, neste caso, a média aritmética não é a melhor medida de centralização para representar esse conjunto de dados, pois a maioria dos salários é bem menor que $1.800,00. Em algumas situações a mediana é um número mais representativo. A mediana é o termo central do rol. Logo, escrevendo o rol dos dados numéricos dessa situação, temos:
(700; 800; 900; 1000; 5600)
Logo, o termo central desse rol é “900”. Então a mediana é igual a 900.
Se acrescentarmos à lista o salário de $1.000,00de outro funcionário, ficaríamos com um número par de dados numéricos. Nesse caso, a mediana seria a média aritmética dos termos centrais:
(700; 800; 900; 1000; 1000; 5600)
Logo a mediana é dada por:
![]()
Interpretação do resultado:
Podemos interpretar esse resultado da seguinte maneira:
Metade dos funcionários ganha menos de $950,00 e a outra metade mais de $950,00.
Generalizando o cálculo da Mediana:
Se n é ímpar, a mediana é o termo central do rol.
Se n é par, a mediana é a média aritmética dos termos centrais do rol.
Importante: Frequência absoluta É o número de vezes que um determinado valor é observado na amostra (a quantidade de vezes que um dado aparece no Rol)
Dessa forma, podemos resumir o cálculo da mediana da seguinte forma:
– os valores da amostra devem ser colocados em ordem crescente ou decrescente;
– se a quantidade de valores da amostra for ímpar, a mediana é o valor central da amostra. Nesse caso, há a mesma quantidade de valores acima e abaixo desse valor;
– se a quantidade de valores da amostra for par, é preciso tirar a média dos valores centrais para calcular a mediana. Nesse caso, 50% dos valores da amostra estão abaixo e 50% dos valores da amostra estão acima desse valor.
Aprofunde seus estudos com a aula do prof. Lucas e depois continue lendo nossa aula!
Moda
Numa turma foram registradas as idades de todos os 25 alunos.
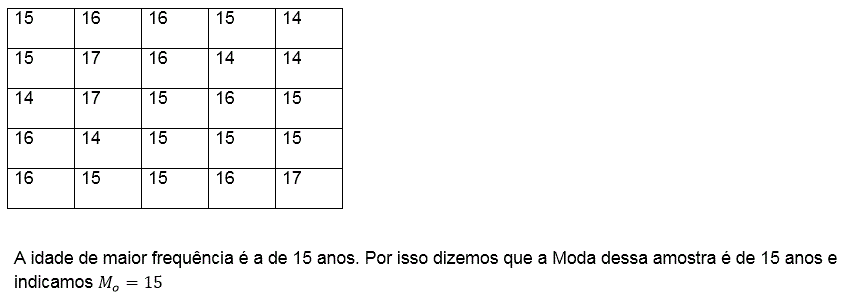
Definição

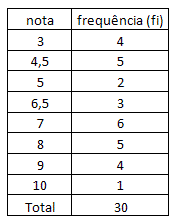
Na coluna da esquerda temos as notas na disciplina de matemática e na coluna da direita, quantos alunos obtiveram a respectiva nota. Dessa forma, podemos observar que a nota que mais aparece nesse conjunto de dados é 7. Portanto,
Mo = 7.
Obs.: amostra bimodal (Pois dois dados aparecem a mesma quantidade de vezes no Rol)
Exemplo
A amostra (1; 3; 5; 7; 9) não apresenta moda, pois todos os elementos tem a mesma frequência.
Dicas: assista nossa videoaula com o professor Sérgio e continue aprendendo conosco!
Venha para o Curso Enem Gratuito:
Criamos para você duas novidades: Um Curso Enem Online totalmente gratuito, e uma bateria de Simulados Enem Gratuitos, com todas as matérias do Exame Nacional do Ensino Médio. Acesse o Curso e faça os Simulados para chegar bem no próximo Enem! Simulados com Gabarito na mesma hora. Veja aqui:
Você pode estudar uma aula gratuita por dia no Curso Enem Online, com todas as matérias do Exame Nacional do Ensino Médio e também as Dicas para uma Redação Enem Nota 1000. Na verdade você pode estudar quantas aulas quiser por dia. Mas, o importante é criar o hábito de ver pelo menos uma aula por dia.
 Curso Enem Gratuito com todas as matérias e dicas de Redação.
Curso Enem Gratuito com todas as matérias e dicas de Redação.
Agora que você já sabe tudo sobre estatística para arrasar no Enem, que tal testar seus conhecimentos?
Exercício – 1 (Enem)

Exercício – 2 (Enem)
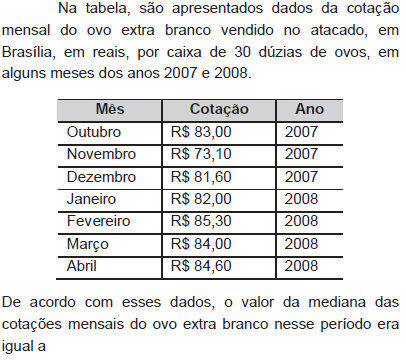
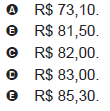
Alternativa D
Exercício – 3 (Enem)
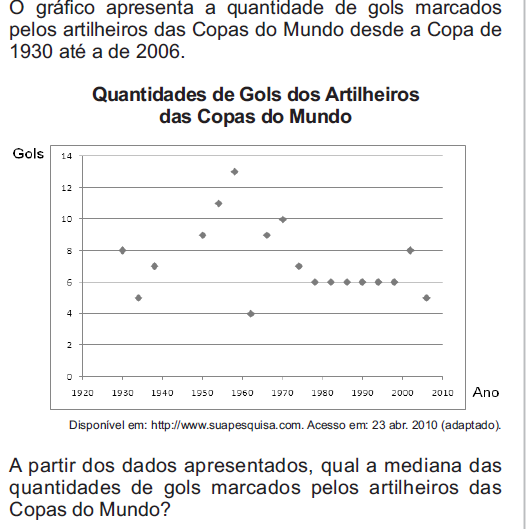
A) 6
B) 6,5
C) 7
D) 7,3
E) 8,5
Alternativa B

