O Enem e os vestibulares sempre cobram questões com equações do 2º grau e fórmula de Bhaskara. Confira nossa lista de exercícios e teste seus conhecimentos!
Equações do segundo grau caem todos os anos no Enem, geralmente dentro de algum problema em que você precisa montar a equação. Por isso preparamos um resumo e uma lista de exercícios sobre equação do 2º grau. Relembre deste conteúdo e teste seus conhecimentos!
Resumo sobre equação do 2º grau
A equação polinomial do 2º grau é toda equação que pode ser escrita na forma:
ax² + bx + c = 0
Veja estes dois exemplos de equações do 2º grau:
2x² – 5x + 3 = 0
e
-x² + 9 = 0
Dentre as várias maneiras de solucionar esse tipo de equação, temos como a mais comum e mais utilizada a fórmula de Bhaskara. Para utilizar essa fórmula, primeiramente você deverá calcular o valor do delta (∆), através da equação:
∆ = b² – 4ac
Onde a, b e c são os coeficientes da equação.
Em seguida, você o substituirá na equação abaixo, para obter os valores das raízes da equação, ou seja, os valores do x.
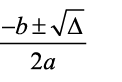
Exemplo
Encontre a solução da equação 2x² -5x +3 = 0.
Temos que os coeficientes da equação são:
- a = 2
- b = -5
- c = 3
Substituímos os valores na fórmula de delta e obtemos o seguinte:
∆ = b² – 4ac
∆ = (-5)² – 4 . 2 . 3
∆ =1
Em seguida, aplicamos o restante da fórmula:
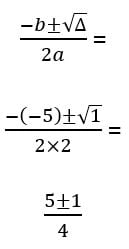
O sinal ± é utilizado para expressar um número que pode ser tanto positivo quanto negativo. Dessa forma, precisamos calcular os dois resultados possíveis para esta equação. Primeiramente vamos calcular com a soma:
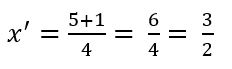
Em seguida, calculamos com a subtração:
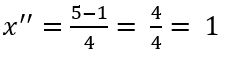
Portanto, a solução é S = {3/2, 1}.
Videoaula sobre fórmula de Bhaskara
Antes de ir para os exercícios sobre equação do 2º grau, confira na videoaula do professor Sarkis como utilizar a fórmula de Bhaskara. Ele traz vários exemplos:
Exercícios sobre equação do 2º grau
Em seguida, confira questões que já caíram no Enem e em vestibulares. Se ficar na dúvida, confira outras formas de resolver equações de 2º grau logo depois dos exercícios!
-
1. Pergunta
(UDESC SC/2018)
A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:
-
2. Pergunta
(UNIFAP AP/2015)
Ainda estudando sobre equações do segundo grau. Tentam resolver o seguinte problema.
O produto de dois números é igual a –128 e a soma destes números dividido por 4 é igual a 7, quais são esses números.
Qual é a alternativa que eles devem marcar como correta: -
3. Pergunta
(IFAL/2017)
Determine o valor de k para que a equação x² + kx + 6 = 0 tendo como raízes os valores 2 e 3.
-
4. Pergunta
(IFBA/2017)
Durante as competições Olímpicas, um jogador de basquete lançou a bola para o alto em direção à cesta. A trajetória descrita pela bola pode ser representada por uma curva chamada parábola, que pode ser representada pela expressão:
h = –2x2 + 8x
(onde “h” é a altura da bola e “x” é a distância percorrida pela bola, ambas em metros)A partir dessas informações, encontre o valor da altura máxima alcançada pela bola:
-
5. Pergunta
(UNISC RS/2015)
A soma de todas as raízes da equação:
(2x² + 6x – 20).(5x – 1) = 0 é -
6. Pergunta
(IFAL/2017)
Determine o valor de k na equação
x² – 12x + k = 0, de modo que uma raiz seja o dobro da outra: -
7. Pergunta
(IFSC/2017)
Pedro é pecuarista e, com o aumento da criação, ele terá que fazer um novo cercado para acomodar seus animais. Sabendo-se que ele terá que utilizar 5 voltas de arame farpado e que o cercado tem forma retangular cujas dimensões são as raízes da equação x² – 45x + 500 = 0, qual a quantidade mínima de arame que Pedro terá que comprar para fazer esse cercado?
Assinale a alternativa CORRETA.
-
8. Pergunta
(UNIFOR CE/2018)
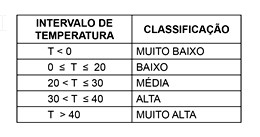
Júlia, aluna do curso de Biologia, está pesquisando o desenvolvimento de certo tipo de bactéria. Para a realização dessa pesquisa, ela utiliza um tipo de estufa para armazenar as bactérias.Sabe-se que dentro da estufa a temperatura em graus Celsius é dada pela equação T(h) = –h2 + 20h – 65 onde h representa as horas do dia. Júlia sabe também que o número de bactérias será o maior possível quando a estufa atinge sua temperatura máxima, e nesse exato momento ela deve tirar as bactérias da estufa.
Baseado na tabela acima, podemos afirmar que a estudante obtém o maior número de bactérias, quando a temperatura no interior da estufa está classificada como
-
9. Pergunta
(IFSC/2017)
Dada a equação quadrática 3x2 + 9x – 120 = 0, determine suas raízes.
Assinale a alternativa que contém a resposta CORRETA. -
10. Pergunta
(IFMA/2016)
As raízes da equação v² + 8v + k = 0 são os números v1 e v2, onde k é uma constante real. Se v1 -3v2 , o valor da constante k é:
Soma e produto
Saiba como resolver equações do 2º grau por meio da técnica da soma e do produto na videoaula do Curso Enem Gratuito:
