Aprenda a resolver questões de Sistemas Lineares. Confira no resumo aulas com exercícios resolvidos para você mandar bem nas provas de Matemática Enem, Encceja e nos vestibulares
Revisão sobre Sistemas Lineares. É Matemática para o Enem e o Vestibular. Confira abaixo a parte teórica, um resumo de introdução, e veja também exercícios resolvidos para você perder o medo e gabaritar nas provas.
Você se recorda das aulas e demonstrações de Sistemas Lineares? Vamos lá recuperar este conteúdo: Um Sistema Linear nada mais é do que um conjunto de ‘p’ equações com ‘n’ variáveis que vão de x1, x2, x3,…., até xn . Estas equações formam um sistema linear com ‘p’ equações e ‘n’ incógnitas.
Exemplo de um Sistema Linear: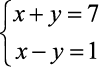
Introdução aos Sistemas Lineares
Veja com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, como você pode resolver e maneira bem rápida as questões de SIstemas Lineares.
Valeu pra você esta introdução, e já comresoluções? Então, agora é hora de avançar. Bora!
Classificação dos Sistemas Lineares:
- Todo sistema linear é classificado de acordo com o número de soluções apresentadas por ele. Veja:
- SPD – Sistema Possível e Determinado – possui apenas uma solução.
- SPI – Sistema Possível e Indeterminado – possui infinitas soluções.
- SI – Sistema Impossível – não possui solução.
Como resolver Sistemas Lineares
Veja um resumo simples e rápido com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, sobre como resolver questões de Sistemas Lineares para mandar bem nas provas de Matemática.
Muito bom este resumo. Show mesmo, pois mostra que dá sim pra resolver bem estes problemas.
Exercício Resolvido de Sistemas Lineares:
Exercício Resolvido 1.(Unisinos 2012) Numa loja, todas as calças têm o mesmo preço, e as camisas também, sendo o preço de uma calça diferente do de uma camisa. Ricardo comprou 1 calça e 2 camisas e pagou R$240,00. Roberto comprou 2 calças e 3 camisas e pagou R$405,00. Qual o preço, em reais, de uma calça e uma camisa, respectivamente?
a) 70 e 95. b) 75 e 90. c) 80 e 85. d) 85 e 80. e) 90 e 75.
- Vamos resolver juntos, para você acompanhar o raciocínio:
- Preço da calça: x
- Preço da camisa: y
- Com as informações do problema, escrevemos o sistema linear.

Resolvendo o sistema, temos: x = 90 e y = 75
Portanto, o valor da calça será R$90,00 e o da camisa R$75,00. Resposta da questão 1: [E]
Exercício Resolvido 2.
(Uerj 2012) Uma família comprou água mineral em embalagens de 20 L, de 10 L e de 2 L. Ao todo, foram comprados 94 L de água, com o custo total de . Veja na tabela os preços da água por embalagem:
|
Volume da embalagem (L) |
Preço (R$) |
|
20 |
10,00 |
|
10 |
6,00 |
|
2 |
3,00 |
Nessa compra, o número de embalagens de 10 L corresponde ao dobro do número de embalagens de 20 L, e a quantidade de embalagens de 2 L corresponde a n.
O valor de n é um divisor de:
a) 32 b) 65 c) 77 d) 81
Vamos resolver juntos, para você confirmar o seu aprendizado: Sejam x, y e z respectivamente, os números de embalagens de 20 L, 10L e 2L.
Do enunciado e da tabela, obtemos
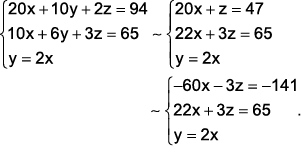
- Adicionando as duas primeiras equações do último sistema, vem:

- Logo, da segunda equação do sistema, encontramos

- Portanto, como
 e
e  , segue que
, segue que  é um divisor de
é um divisor de  Resposta da questão 2: [C]
Resposta da questão 2: [C]
Como resolver equações de Primeiro Grau
Veja agora no resumo de Matemática como resolver equações de Primeiro Grau.
Excelente resumo. É do canal do Curso Enem Gratuito. Agora, bora resolver mais problemas para dominar bem o conteúdo.
Desafios de Sistemas Lineares para você resolver e compartilhar
Questão 1
(Unicamp 2012) As companhias aéreas costumam estabelecer um limite de peso para a bagagem de cada passageiro, cobrando uma taxa por quilograma de excesso de peso. Quando dois passageiros compartilham a bagagem, seus limites são considerados em conjunto.
Em um determinado voo, tanto um casal como um senhor que viajava sozinho transportaram 60 kg de bagagem e foram obrigados a pagar pelo excesso de peso. O valor que o senhor pagou correspondeu a 3,5 vezes o valor pago pelo casal.
Para determinar o peso excedente das bagagens do casal (x) e do senhor que viajava sozinho (y), bem como o limite de peso que um passageiro pode transportar sem pagar qualquer taxa (z), pode-se resolver o seguinte sistema linear:
a)
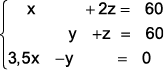
b)
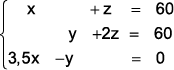
c)
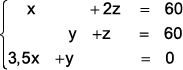
d)
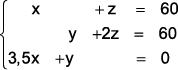
Dica 1 – Estude sobre Circunferência em mais esta aula de revisão para Matemática Enem. O Exame Nacional do Ensino Médio está chegando, estude com a gente! – https://blogdoenem.com.br/circunferencia-matematica-enem/
Questão 2
(Fuvest 2012) Em uma festa com n pessoas, em um dado instante, 31 mulheres se retiraram e restaram convidados na razão de 2 homens para cada mulher. Um pouco mais tarde, 55 homens se retiraram e restaram, a seguir, convidados na razão de 3 mulheres para cada homem. O número n de pessoas presentes inicialmente na festa era igual a
- a) 100
- b) 105
- c) 115
- d) 130
- e) 135
Dica 2 – Preparado para o Exame Nacional do Ensino Médio? Revise tudo sobre Geometria Analítica em mais uma aula de Matemática Enem que preparamos para você – https://blogdoenem.com.br/geometria-analitica-matematica-enem/
Questão 3
(G1 – ifpe 2012) Com a proximidade do final do ano, uma papelaria quis antecipar as promoções de material didático para o ano letivo de 2012. Foram colocados em promoção caneta, caderno e lápis. As três ofertas eram:
1ª) 5 canetas, 4 cadernos e 10 lápis por R$ 62,00;
2ª) 3 canetas, 5 cadernos e 3 lápis por R$ 66,00;
3ª) 2 canetas, 3 cadernos e 7 lápis por R$ 44,00.
Para comparar os preços unitários dessa papelaria com outras do comércio, o Sr. Ricardo calculou os preços de uma caneta, um caderno e um lápis. A soma desses preços é:
- a) R$ 20,00
- b) R$ 18,00
- c) R$ 16,00
- d) R$ 14,00
- e) R$ 12,00
Dica 3 – Revise sobre as Funções Trigonométricas em mais esta aula preparatória para prova de Matemática Enem. Estude conosco para o Exame Nacional do Ensino Médio! – https://blogdoenem.com.br/funcoes-trigonometricas-matematica-enem/
Questão 4
(G1 – ifce 2012) A soma de dois números naturais é 561. O maior é igual à diferença entre o dobro do menor e 231. O máximo divisor comum entre esses números é
- a) 27.
- b) 33.
- c) 81.
- d) 121.
- e) 792.
Questão 5
(Ufrgs 2012) Inovando na forma de atender aos clientes, um restaurante serve alimentos utilizando pratos de três cores diferentes: verde, amarelo e branco. Os pratos da mesma cor custam o mesmo valor. Na mesa A, foram consumidos os alimentos de 3 pratos verdes, de 2 amarelos e de 4 brancos, totalizando um gasto de R$ 88,00. Na mesa B, foram consumidos os alimentos de 2 pratos verdes e de 5 brancos, totalizando um gasto de R$ 64,00. Na mesa C, foram consumidos os alimentos de 4 pratos verdes e de 1 amarelo, totalizando um gasto de R$ 58,00.
Comparando o valor do prato branco com o valor dos outros pratos, verifica-se que esse valor é
- a) 80% do valor do prato amarelo.
- b) 75% do valor do prato amarelo.
- c) 50% do valor do prato verde.
- d) maior que o valor do prato verde.
- e) a terça parte do valor da soma dos valores dos outros pratos.
Você consegue resolver estes exercícios de Sistemas Lineares? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
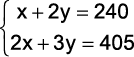
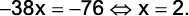
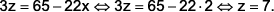
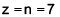 e
e 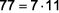 , segue que
, segue que 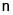 é um divisor de
é um divisor de 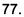 Resposta da questão 2: [C]
Resposta da questão 2: [C]


