Tire todas as suas dúvidas sobre os cálculos envolvendo uma Pirâmide e o 'Tronco de Pirâmide'. Revisão gratuita de matemática com a teoria, exemplos e exercícios para você. Confira.
Confira o que é o Tronco de Pirâmide para aprender os elementos clássicos, e os cálculos básicos. que mais caem nas provas. Observe agora que através de uma secção (corte) paralela ao plano que contém a base da pirâmide, obtemos uma pirâmide menor.
Veja na imagem a seguir: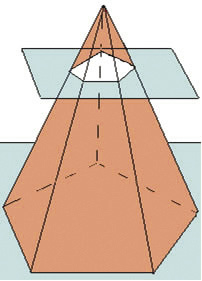
A figura que se forma abaixo da secção chama-se tronco de pirâmide. Você compreendeu o que é ‘abaixo da secção’?
O Tronco da Pirâmide
Se você ainda teve dúvidas, veja agora esta nova imagem, na sequência.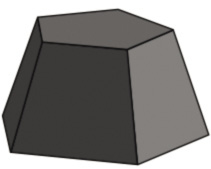
Ficou mais fácil de compreender, agora? Com a imagem ajudando a visualizar o que se trabalha na teoria se aprende mais fácil, concorda?
O Tronco da Pirâmide, portanto, nada mais é do que a parte abaixo do corte que ‘seccionou’ a figura original. Esta parte de baixo se chama Tronco da Pirâmide, e é muito útil para solucionar cálculos envolvendo Pirâmides.
Resumo sobre Pirâmide
Veja com o professor Sérgio Sarkis, do canal do Curso Enem Gratuito, o básico que você precisa para gabaritar nas questões de cálculo de Área, Volume, Aresta, ou de Tronco de Pirâmide.
As dicas sobre as Pirâmides na Matemática:
- Acompanhe no vídeo como se calculam as áreas e o volume da pirâmide.
- Veja quais são as áreas que podemos calcular? A área da base, a área lateral e a área total. Vamos ver como se calcula cada uma delas o/
- Quando a gente fala da base da pirâmide, estamos falando do polígono que forma essa base. Sendo assim, a área da base de uma pirâmide depende do polígono que a forma – e que, lembrando, dá nome a ela.
- A área lateral é a área que circunda a figura. Corresponde à soma das áreas das faces laterais. Veja como calculá-la!
- Lembrando que a quantidade de faces da pirâmide é sempre igual ao número de lados da base.
- Se a pirâmide for regular, você pode utilizar uma fórmula para calcular sua área lateral (confira na lousa, no vídeo acima).
Elementos principais para os cálculos envolvendo Pirâmides: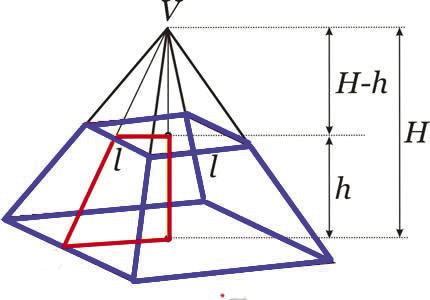
- Os elementos clássicos para os cálculos nas Pirâmides:
- L = aresta da base maior;
- l = aresta da base menor;
- H = altura da pirâmide maior;
- h = altura da pirâmide menor.
As fórmulas para o cálculo de Pirâmide
Para resolver os problemas devemos lembrar que as pirâmides maior e menor são semelhantes e portanto suas medidas são proporcionais.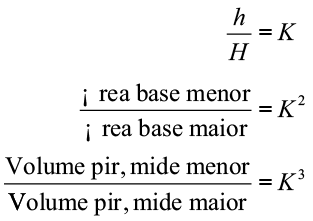
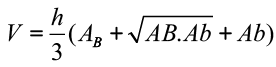Para você compreender os elementos da fórmula, vamos esclarecer cada um deles: h = altura do tronco; AB = área da base maior; Ab = área da base menor.
Veja também uma aula sobre como calcular área e volume de cilindros:
.
Desafios sobre Pirâmides. Resolva e compartilhe
Questão 01
Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19cm de altura e 6cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura – 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior -, espaçados de 1cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.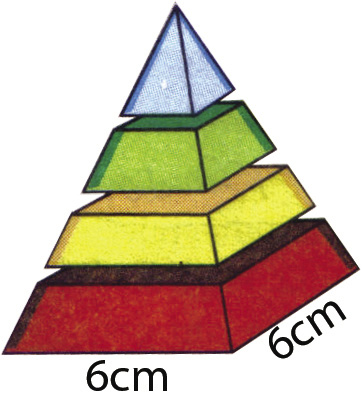
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide de parte superior, que tem 1,5cm de aresta de base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
- a) 156cm³
- b) 189cm³
- c) 192cm³
- d) 216cm³
- e) 540cm³
Dica 2 – Relembre sobre o conceito e os tipos de Cilindros nesta aula preparatória para a prova de Matemática Enem. Estude conosco e fique preparado para o Exame! – https://blogdoenem.com.br/cilindro-matematica-enem/
Questão 02 – PirÂamide
Uma estátua está colocada sobre um pedestal de concreto em forma de tronco de pirâmide quadrangular regular. As arestas das bases são 5m e 12m, e sua altura é de 8m. Qual foi (aproximadamente) o volume de concreto utilizado para construir este pedestal?
- a) 500m³
- b) 550 m³
- c) 610m³
- d) 800m³
- e) 890m³
Questão 03
Em São Paulo, no Parque do Ibirapuera, há um monumento de concreto chamado de Obelisco aos Heróis de 1032, uma homenagem aos que morreram na Revolução Constitucionalista de 1932.
Esse monumento tem a forma de um tronco de pirâmide de base quadrada e tem 72m de altura. Suas bases possuem arestas de 9m e 7m.
Determine o custo de concreto utilizado na construção do Obelisco sabendo que o preço do metro cúbico de concreto utilizado na obra é de R$ 250,00.
- a) R$ 800.000,00
- b) R$ 1.000.000,00
- c) R$ 1.158.000,00
- d) R$ 1.500.000,00
- e) R$ 2.200.000,00
Tronco de cone
Através de uma secção (corte) paralela ao plano que contém a base do cone obtemos um cone menor.
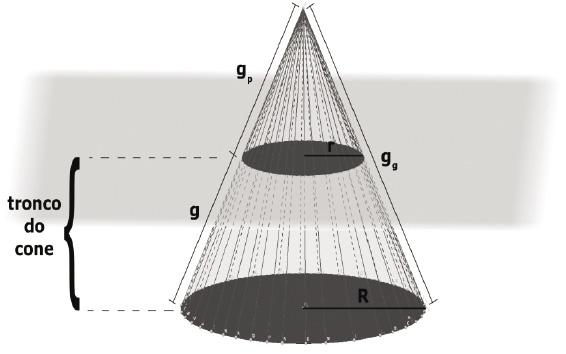
Elementos principais
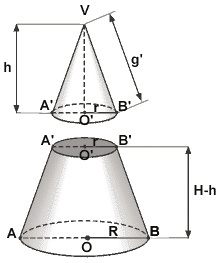
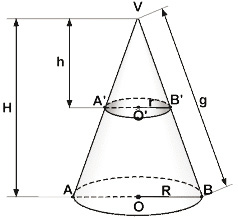
H = altura cone maior
h = altura cone menor
g = geratriz maior
g’ = geratriz menor
R = raio maior
r = raio menor
É possível verificar que:
- Área lateral do tronco de cone
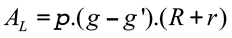
- Volume do tronco
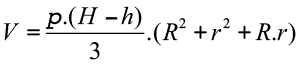
Desafios
Questão 04
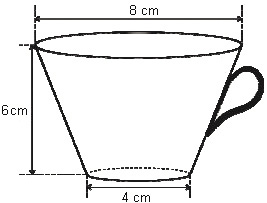
Considere uma jarra com 1 litro de leite e uma xícara com as medidas conforme a figura. Quantas xícaras iguais a essa são necessárias para esvaziar complemente a jarra?
a) 3
b) 4
c) 5
d) 6
e) 7
Dica 3 – Se você ainda não sabe o que é um poliedro, e que as Pirâmides são poliedros, então preparamos esta aula para você gabaritar na prova de Matemática Enem – https://blogdoenem.com.br/piramide-matematica-enem/
Questão 05
Um reservatório de água tem a forma de um cone circular reto, de eixo vertical e vértice para baixo. Quando o nível de água atinge a metade da altura do tanque, o volume ocupado é igual a π. Determine a capacidade do tanque (considere π = 3).
a) 18
b) 20
c) 22
d) 24
e) 26
Você consegue resolver estes exercícios sobre Pirâmide? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão.
Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
