Revise tudo sobre os Logaritmos em mais esta aula de Matemática Enem, com definições e exercícios resolvidos para você gabaritar no Exame Nacional do Ensino Médio
Veja a definição clássica de Logaritmos: o cálculo do logaritmo de um determinado número positivo ‘b’ numa base ‘a’ que seja positiva e diferente de ‘1’ é representado na seguinte fórmula: logab = x
Veja agora os termos de logab = x: a = base do logaritmo; b = logaritmando; x = logaritmo. Veja agora os fundamentos de validação da definição em representação matemática: sendo b > 0, a > 0 e a ≠ 1
Explicando agora para você compreender a definição: O logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base a para se obter o número b. Dessa forma, então: logab = x ↔ ax = b.
O uso de escalas logarítmicas pode ser aplicado para reduzir grandezas de alta amplitude para menores valores. Quando você ler a respeito da dimensão ‘decibel’ (ou decibéis) em relação à medida de intensidade do som, estará diante de uma aplicação de logaritmos para se chegar ao cálculo realizado.
Neste caso, a medida do som em decibéis indica ‘a proporção de uma quantidade física (energia ou intensidade) em relação a uma referência. Ou seja, representa a razão entre a quantificação da energia liberada e a amplitude mensurada (fonte Wiki).
Consequências da definição de logaritmo:
loga1 = 0
logaa = 1
logaam = m
alogªb = b
logab = logac ↔ b = c
Exercício resolvido de Logaritmo:
Calcule: Log5625 + Log100 – Log327:
Vamos calcular cada um dos logaritmos separadamente.
O Log5625 é o expoente da potência de base 5 que resulta em 625: log5625 = x
5x = 625
Pode-se resolver a equação exponencial decompondo 625 em fatores primos:
Ou seja, 625 = 54, o que nos leva ao valor de x: 5x = 625 / 5x = 54 / x = 4.
Assim, calculou-se o valor de x desta forma, pois a base 5 é positiva e diferente de 1. Se você não se lembra disto, convém consultar o tema equação exponencial para recordar esta matéria.
Então 4 é o Log5625:
Dicas de Logaritmo:
O Log 100 é o expoente da potência de base 10 que resulta em 100:
log100 = x ⇔ 10x =100
O valor de x agora é óbvio.
Como se sabe, uma potência de dez com expoente natural resulta em um número começando pelo algarismo 1 seguido de tantos zeros quantos indicados por este expoente.
Sabendo-se disto, se o número 100 possui 2 zeros após o 1 é porque o expoente da potência de base dez é igual a dois (102 =100), isto é, x = 2.
Então, 2 é o Log 100:
Por último, o Log327 é igual a 3, pois este é o expoente ao qual se deve elevar a base também 3 para se obter 27:
log327 = 3 ⇔ 33 = 27
Se você tem dúvidas quanto a isto, também pode decompor o número 27 em fatores primos assim como foi feito com o Log5625.
Realizando as substituições na expressão original, obtém-se:
log5625 + log 100 – log3 27 ⇔ 4 + 2 – 3 = 3
Log5625 + Log 100 – Log327 = 3.
Aulas Gratuitas
Desafios
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
Questão 1
O valor de 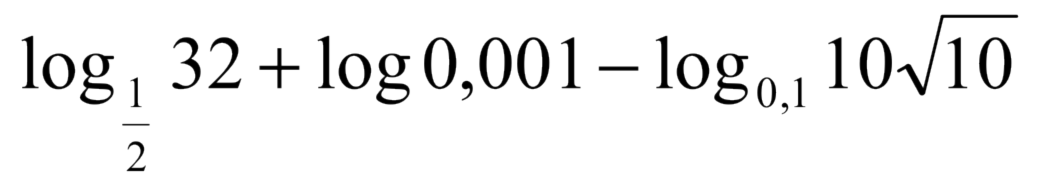 é:
é:
a) – 13
b) – 13/2
c) – 19/2
d) – 19
e) – 22/3
Dica 1 – Pronto para o Exame Nacional do Ensino Médio? Revise tudo sobre Função Exponencial em mais esta aula preparatória para a prova de Matemática Enem! – https://blogdoenem.com.br/funcao-exponencial-matematica-enem/
Questão 2
(UEL) O valor da expressão
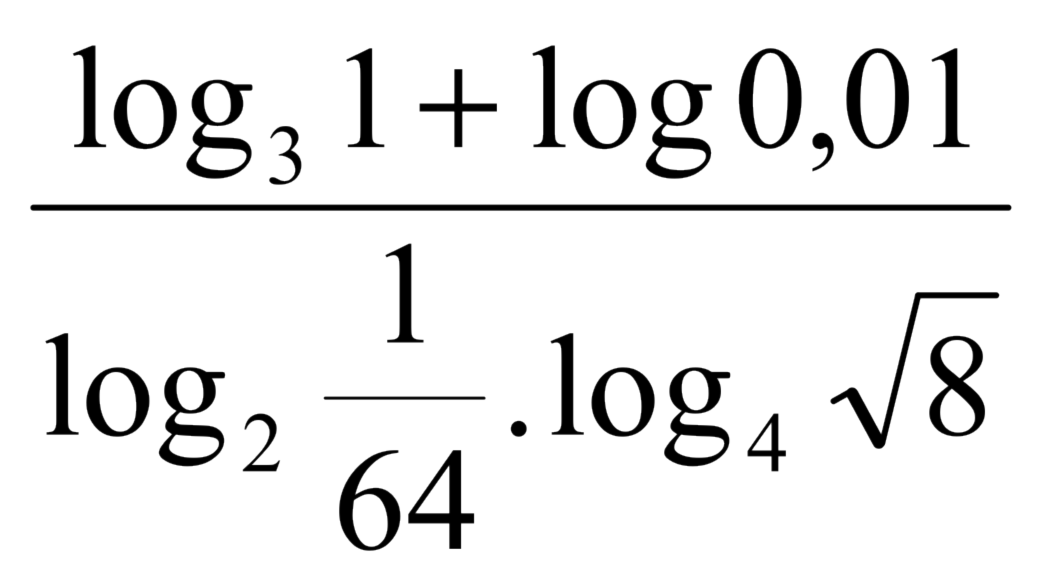 é:
é:
a) 4/15
b) 1/3
c) 4/9
d) 3/5
e) 2/3
Dica 2 – O Exame Nacional do Ensino Médio está chegando! Revise sobre Equações Exponenciais para garantir uma boa nota na prova de Matemática Enem – https://blogdoenem.com.br/equacoes-exponenciais-matematica-enem/
Questão 3
(UFPA) O valor do
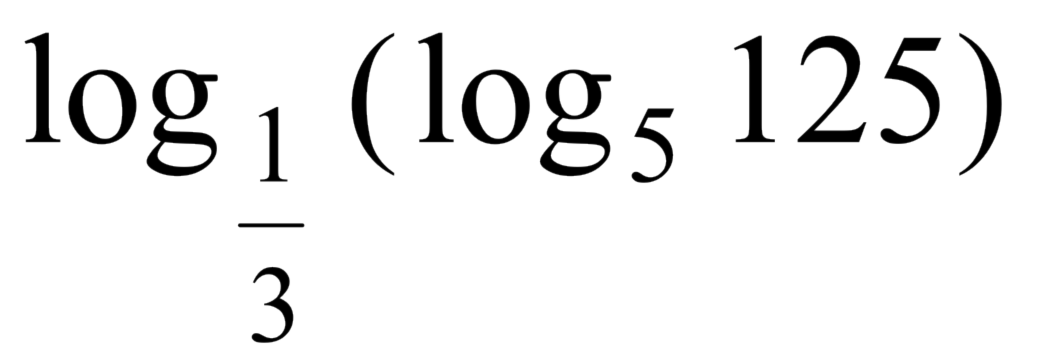
é:
a) 1
b) – 1
c) 0
d) 2
e) 0,5
Questão 4
(MACK) O valor de
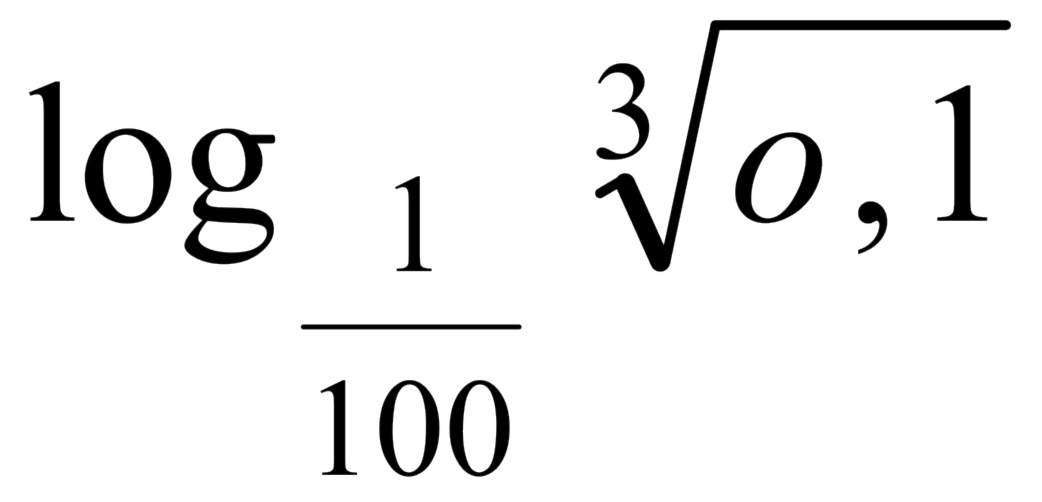 é:
é:
a) – 1/2
b) – 1/6
c) 1/6
d) 1/2
e) 1
Dica 3 – Com o Enem chegando você não sabe mais o que estudar? Então, revise sobre Potencialização e Radiciação em mais esta aula de Matemática Enem – https://blogdoenem.com.br/potenciacao-e-radiciacao-matematica-enem/
Questão 5
(MACK) Se
y = 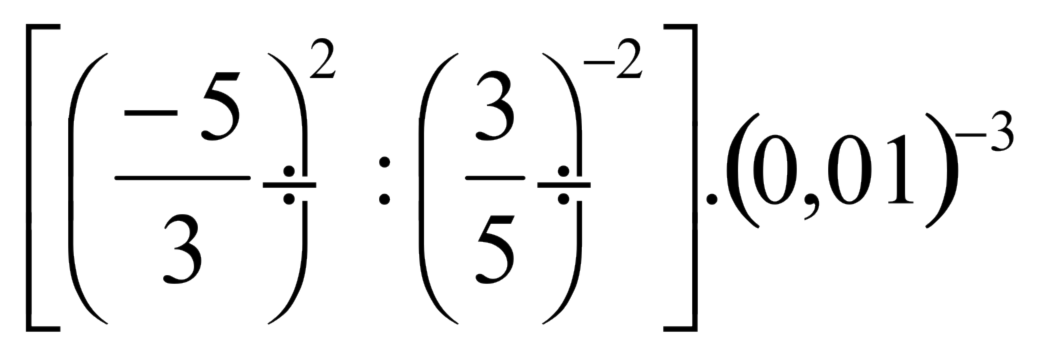 ,
,
então log100vale:
a) 5
b) 2
c) 7
d) 3
e) 6

