Veja as Funções Trigonométricas Seno, Cosseno, Tangente e Cotangente nesta aula preparatória para prova de Matemática Enem e do vestibular tambem. Vem!
Você se lembra das aulas sobre Funções Trigonométricas? Seno e Cosseno, na ponta da língua? Não, então é hora de revisar com aula grátis e com exercício resolvido aqui no Blog do Enem.
Na aula de hoje as funções Seno e Cosseno serão definidas conceitualmente e geometricamente por meio dos seus gráficos. Serão abordados ainda as variações de seu sinal no ciclo trigonométrico e algumas propriedades. Confira e arrase em matemática no Enem e nos vestibulares.
É hora de mergulhar mais fundo e aprender (ou lembrar) Seno e Cosseno. Vamos considerar o triângulo da figura abaixo: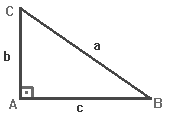
Em um triângulo retângulo, temos dois lados que formam ângulos com a hipotenusa, então para não criar confusões, denomina-se o lado sempre tomando como referência o ângulo ao qual ele está relacionado.
Para isso, acompanhe a tabela a seguir: 
O lado adjacente, na tabela acima, é o lado que descreve o ângulo junto com a hipotenusa.
Introdução à Lei do Seno
Veja agora com o professor Lucas Borguesan, do canal do Curso Enem Gratuito, um resumo para você dominar a aplicação da Lei do Seno.
A lei dos senos é usada quando temos um triângulo e sabemos os valores de dois ângulos e um lado. Quando temos os valores de dois lados e um ângulo, usamos a lei dos cossenos.
A lei dos senos diz o seguinte: se eu tenho um lado qualquer e divido pelo seno do ângulo que enxerga esse lado, isso é igual que um outro lado dividido pelo seno do seu ângulo. Ou seja, a fórmula da lei dos senos é: a / sen(A) = b / sen(B) = c / sen(C).
Veja na aula acima, na prática, como é mais simples d eentender com o apoio do professor Lucas, e as resoluções de exercícios no quadro. Confira agora.
Agora que você já entendeu o processo descrito acima, vamos trabalhar a ideia principal desse post. Para isso, vamos contextualizar um pouco a motivação deste estudo.
O Processo histórico da Trigonometria
A essa altura, você já deve saber que a Matemática sempre andou de mãos dadas com a Astronomia, Agrimensura e as Navegações. E, por conta dessa proximidade, muitos dos problemas que surgiram com essas ciências utilizaram recursos da Álgebra e Geometria para encontrar suas respectivas soluções.
Por exemplo, no ENEM de 2009, caiu uma questão interessante que envolvia três irmãos que dividiriam uma herança com uma área de extração de ouro delimitada por uma região circular. Se tomarmos emprestado uma parte desse problema, teríamos a seguinte figura geométrica: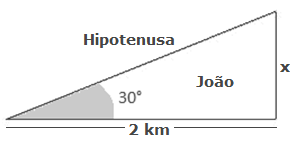
Para encontrar o valor do lado X deste triângulo usaremos as relações trigonométricas, pois com elas podemos associar as razões entre dois lados (oposto e adjacente) a uma medida específica de cada ângulo.
No nosso caso, podemos fazer três associações:
|
Ângulo |
1ª Razão |
2ª Razão |
3ª Razão |
|
30° |
x/hipotenusa |
2/hipotenusa |
x/2 |
Para a 1ª razão, damos o nome de SENO. Já para a 2ª razão, damos o nome de COSSENO e para a 3ª razão, damos o nome de TANGENTE.
.
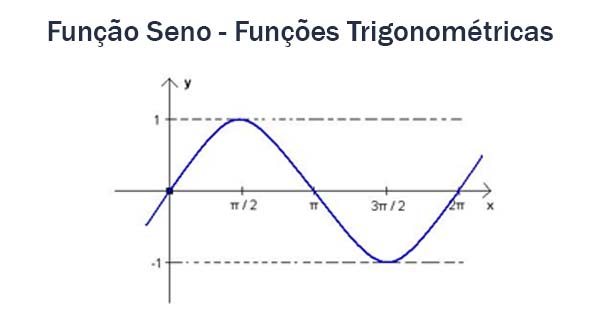
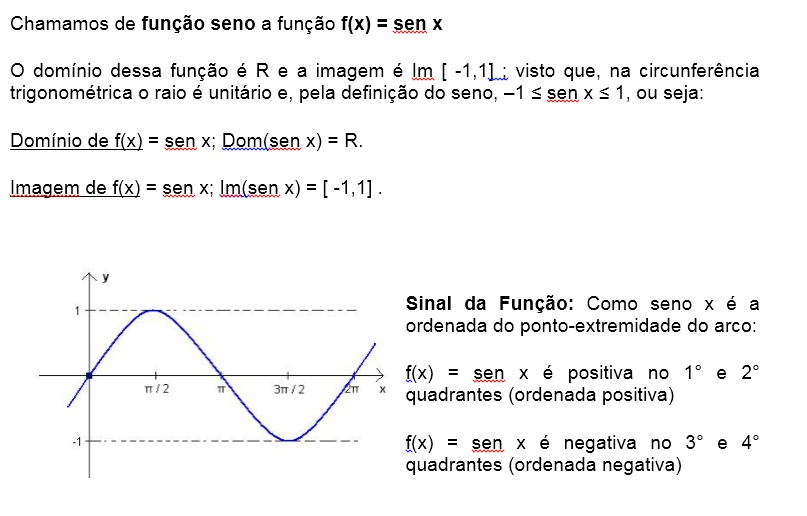
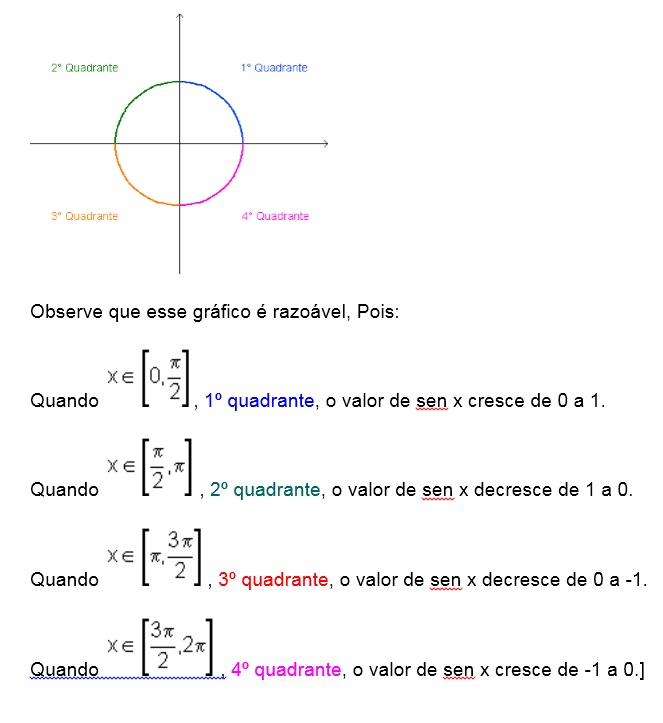
Variação da função seno
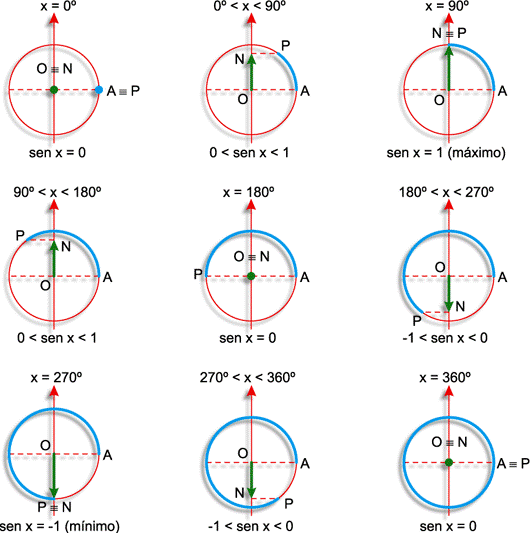
Confira agora o Gráfico da Função Seno. Você vai “bater o olho” e entender o que significa uma “senoide”
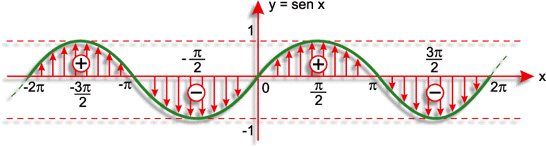
Introdução à Função Cosseno
Acompanhe com o professor Lucas Borguesan, a Lei do Cosseno.
- A lei dos cossenos é usada quando temos um triângulo e só sabemos os valores de dois dos seus lados e o valor de um dos ângulos.
- Se for um triângulo retângulo, ou seja, um triângulo com um ângulo reto, seria possível resolver o problema com o Teorema de Pitágoras.
- Contudo, em outros tipos de retângulos é preciso aplicar a lei dos cossenos. A fórmula da lei dos cossenos, inclusive, é bastante parecida com o Teorema de Pitágoras, então é importante prestar atenção para não confundir as fórmulas.
- A fórmula da lei dos cossenos é a² = b² + c² – 2.b.c.cos(A)
- Na hora de aplicar a lei dos cossenos, lembre-se de que a “hipotenusa” é o lado oposto ao ângulo cujo valor é conhecido. Ou seja, o temos o valor do lado a e o valor do ângulo A, cujo cosseno precisamos descobrir caso o enunciado do exercício não informar.
Veja agora a Função Cosseno
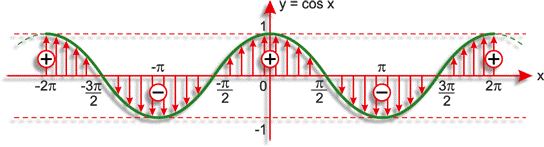
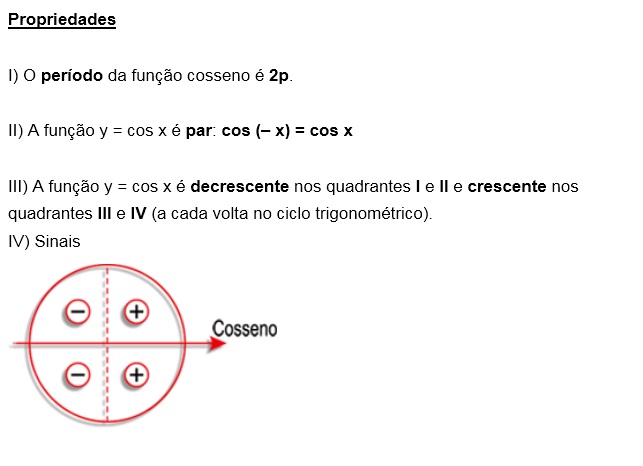
Gráfico
Curso Enem Gratuito
Quer aumentar suas chances no próximo Exame Nacional do Ensino Médio e mandar bem nas Notas de Corte do Enem? Estude com as apostilas e aulas gratuitas do Curso Enem Online. Todas as matérias do Exame e ainda as Dicas de Redação. Acesse aqui o Curso Enem Gratuito Online.
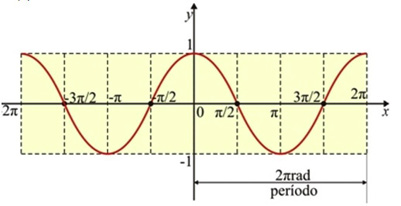
Função Seno se representa assim:
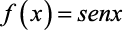
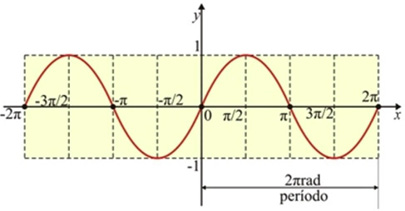
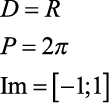
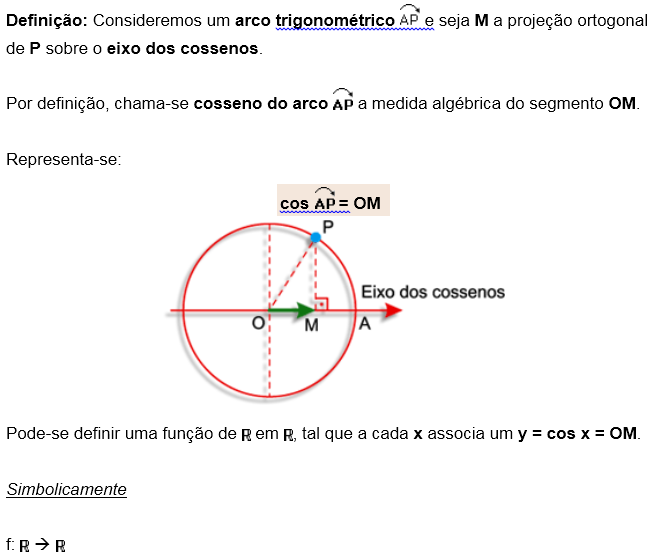
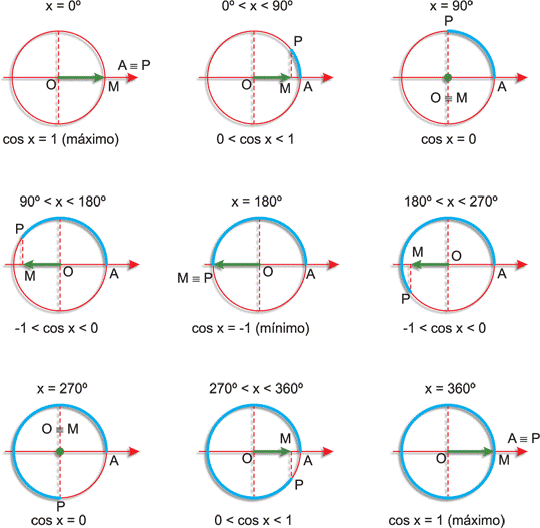
A Função Cosseno é representada assim:
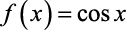
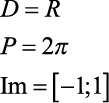
Veja a Função Tangente:
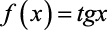
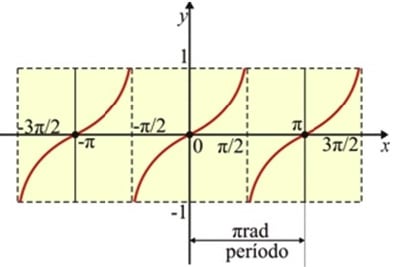
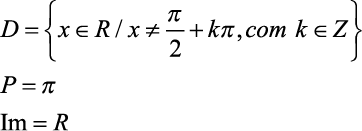
Exercício Resolvido de Trigonometria:
(Ufpb 2011) Com o objetivo de aumentar a produção de alimentos em certa região, uma secretaria de agricultura encomendou a uma equipe de agrônomos um estudo sobre as potencialidades do solo dessa região. Na análise da temperatura do solo, a equipe efetuou medições diárias, durante quatro dias consecutivos, em intervalos de uma hora.
As medições tiveram início às 6 horas da manhã do primeiro dia (t = 0). Os estudos indicaram que a temperatura T, medida em graus Celsius, e o tempo t, representando o número de horas decorridas após o início das observações, relacionavam-se através da expressão
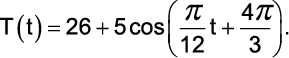
Com base nessas informações, identifique as afirmativas corretas:
( ) A temperatura do solo, às 6 horas da manhã do primeiro dia, foi de 23,5 ºC.
( ) A função T(t) é periódica e tem período igual a 24 h.
( ) A função T(t) atinge valor máximo igual a 30 ºC.
( ) A temperatura do solo atingiu o valor máximo, no primeiro dia, às 14 h.
( ) A função T(t) é crescente no intervalo [0,8].
Veja agora o desenvolvimento da questão:
( V ) T(0) = 26 + 5.(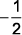
) = 23,5o
( V ) P = 
( F ) Valor máximo = 26 + 5.1 = 31
( V )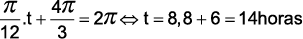 
( V ) começa em 23,5o e vai aumentando até seu valor máximo quando t = 8
Resposta da questão: V V F V V
Aumente suas chances no próximo Enem com as aulas, dicas, exercícios e simulados do Curso Enem Gratuito Online, do Blog do Enem. Todas as matérias do Enem e também as orientações para uma Redação Enem nota 1000. Acesse aqui o Curso Enem Gratuito.
Aula Gratuita:
Saiba mais sobre Funções Trigonométricas nesta aula do Professor Rogério do canal hexagmedicina, disponível no Youtube. Após assistir, revise o que você aprendeu respondendo aos nossos desafios!
Desafios sobre Seno, Cosseno, Tangente e Cotangente para o Enem
Questão 1
(Ufpb 2012) Um especialista, ao estudar a influência da variação da altura das marés na vida de várias espécies em certo manguezal, concluiu que a altura A das marés, dada em metros, em um espaço de tempo não muito grande, poderia ser modelada de acordo com a função:
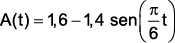
Nessa função, a variável t representa o tempo decorrido, em horas, a partir da meia-noite de certo dia. Nesse contexto, conclui-se que a função A, no intervalo [0,12], está representada pelo gráfico:
a)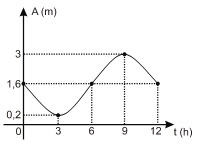 
b)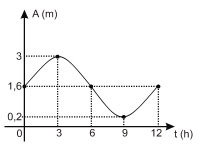
c)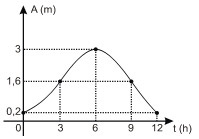
d)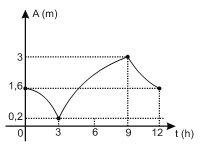
e)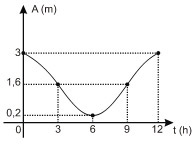
Dica 1 – Preparado para o Exame Nacional do Ensino Médio? Revise sobre Trigonometria para garantir a sua nota na prova de Matemática Enem! – https://blogdoenem.com.br/trigonometria-matematica-enem/
Questão 2
(Ufrgs 2010) O período da função definida por
f(x) = sen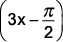 
é
a)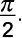 
b)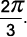 
c)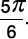 
d)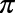 
e) 2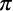 
Dica 2 – Revise sobre Logaritmos: Equação e Função em mais esta aula preparatória para a prova de Matemática Enem. Estude conosco e fique pronto para o Exame! – https://blogdoenem.com.br/logaritmos-equacao-e-funcao-matematica-enem/
Questão 3
(Ufpr 2010) Suponha que o horário do pôr do sol na cidade de Curitiba, durante o ano de 2009, possa ser descrito pela função
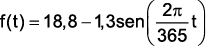
sendo t o tempo dado em dias e t = 0 o dia 1º de janeiro. Com base nessas informações, considere as seguintes afirmativas:
1. O período da função acima é 2π .
2. Foi no mês de abril o dia em que o pôr do sol ocorreu mais cedo.
3. O horário em que o pôr do sol ocorreu mais cedo foi 17h30.
Assinale a alternativa correta.
a) Somente a afirmativa 3 é verdadeira.
b) Somente as afirmativas 1 e 2 são verdadeiras.
c) Somente as afirmativas 1 e 3 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
Dica 3 – Confira a aula sobre Logaritmos que preparamos para você gabaritar na prova de Matemática Enem – https://blogdoenem.com.br/logaritmos-revisao-matematica-enem/
Questão 4
(Ufsm 2008) Em determinada cidade, a concentração diária, em gramas, de partículas de fósforo na atmosfera é medida pela função
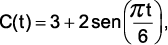
em que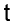 
é a quantidade de horas para fazer essa medição.
O tempo mínimo necessário para fazer uma medição que registrou 4 gramas de fósforo é de
a) 1/2 hora.
b) 1 hora.
c) 2 horas.
d) 3 horas.
e) 4 horas.
Questão 5
(Ufsm 2007) Uma gráfica que confeccionou material de campanha determina o custo unitário de um de seus produtos, em reais, de acordo com a lei C(t) = 200 + 120 . sen (π . t)/2, com t medido em horas de trabalho. Assim, os custos máximos e mínimo desse produto são
a) 320 e 200
b) 200 e 120
c) 200 e 80
d) 320 e 80
e) 120 e 80
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
