Se você ainda não sabe o que é um poliedro, e que as Pirâmides são poliedros, então preparamos esta aula para você gabaritar na prova de Matemática Enem. Veja o que são o Vértice, as Arestas, a Base, a Altura, e os cálculos de área e de volume na Pirâmide.
Se você ainda não sabia, e hora de aprender: Toda Pirâmide é um Poliedro. A tradução de poliedro é ‘muitas faces’, onde apenas uma delas está função de base de apoio.
Veja aqui, escrito de outra forma, para você nunca mais esquecer: A exemplo dos prismas, as pirâmides são poliedros (“muitas faces”) onde apenas uma das faces representa a sua base (ao contrário dos prismas que possuem duas bases iguais e paralelas).
Os triângulos não tem ‘lados’ ou ‘bases’ paralelas.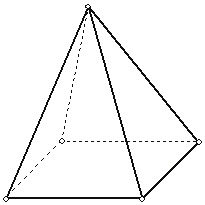
Observe na figura acima e identifique onde está a ‘Base’, e quais são as ‘Faces Laterais’ desta pirâmide.
Conseguiu aprender? Então, esta Pirâmide tem uma base ‘Quadrangular’. agora feche os olhos e faça um exercício de representação mental de pirâmides de bases triangulares ou de bases quadrangulares, identificando a base e as faces.
A exemplo do que estudamos nos prismas, é o polígono da base da pirâmide quem determina o nome dado às pirâmides. Veja agora uma Pirâmide de base triangular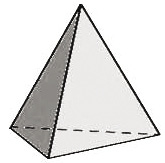
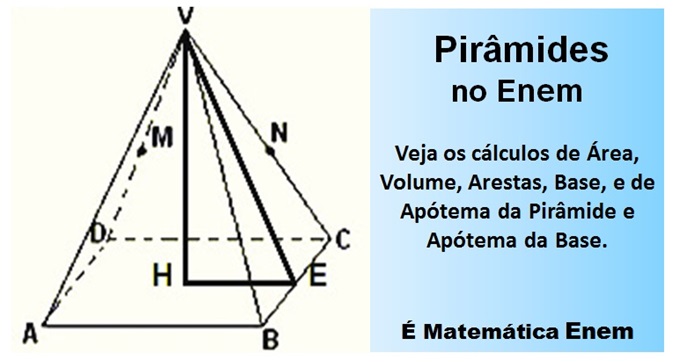
Os Elementos da Pirâmide: Com uma boa dose de observação, anotações, e muita atenção você poderá perceber os diversos elementos de uma Pirâmide e que são utilizados para fazer diversos cálculos.
Você encontra no topo das pirâmides o Vértice. a partir dele diversas medidas podem ser obtidas, tais como as Arestas Laterais, a Areta da Base, a Altura (do vértice descendo na perpendicular da Base), o Apótema da Pirâmide, e ainda pode calcular a Área da Base, da Pirâmide, e também o Volume.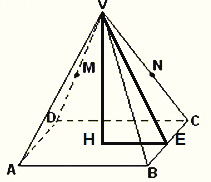
Os elementos da Pirâmide:
- V = vértice
- VA = aresta lateral ( aℓ )
- AB = aresta da base ( ℓ ).
- AH = altura ( h )
- HE = apótema da base ( ab )
- VE = apótema da pirâmide ( ap )
Pirâmide Regular: A pirâmide será do tipo regular quando o polígono da base for regular. Veja a seguir o que são as Pirâmides Triangulares, Quadrangulares, e Hexagonais.
- Pirâmide Triangular Regular: a base é um triângulo equilátero.
- Pirâmide Quadrangular Regular: a base é um quadrado.
- Pirâmide Hexagonal Regular: a base é um hexágono regular.
Áreas e volume (Pirâmide regular)
Área da base (AB)
Calculada de acordo com o nome da pirâmide. Veja como calcular:
Considere ℓ como a aresta da base.
- Pirâmide Triangular Regular:
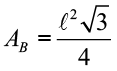
- Pirâmide Quadrangular Regular:
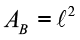
- Pirâmide Hexagonal Regular:
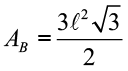
Área lateral (AL)
As faces são triangulares, assim basta calcular a área de uma face e multiplicar o valor pelo número de faces (sempre igual ao número de lados da base ).
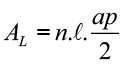
Área total (AT)
Corresponde à soma da área lateral com as duas bases do prisma.
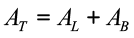
Volume (V)
É o resultado da multiplicação da área da base pela altura do prisma.
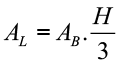
Relação auxiliar
Observe que o triângulo VHE é retângulo; assim podemos aplicar o teorema de Pitágoras:
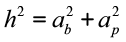
Continue estudando o volume e a área das pirâmides com a aula:
Desafios para você resolver e compartilhar
Questão 01
Uma pirâmide hexagonal tem:
a) 6 vértices.
b) 7 faces triangulares.
c) 7 arestas.
d) 12 arestas.
e) 12 vértices.
Dica 1 – Nesta aula de revisão para a prova de Matemática Enem você vai estudar a classificação, as nomenclaturas e os cálculos de volume e áreas dos Prismas – https://blogdoenem.com.br/estudo-dos-prismas-matematica-enem/
Questão 02
Talvez não seja inútil conhecer as dimensões de pirâmides do antigo Egito. A maior delas, Quéops, é uma pirâmide regular de base quadrada, com 138m de altura e 23m na aresta da base. Esses dados permitiram que fosse calculado o volume de uma pirâmide, semelhante à de Quéops, para ser usada como um peso para papel. Se a área da base dessa pequena pirâmide é 100cm2, o seu volume, em centímetros cúbicos, é:
a) 200
b) 250
c) 300
d) 360
e) 400
Dica 2 – Você sabe tudo sobre os Polígonos Regulares? Revise as suas definições e classificações em mais uma aula de Matemática Enem – https://blogdoenem.com.br/poligonos-regulares-matematica-enem/
Questão 03
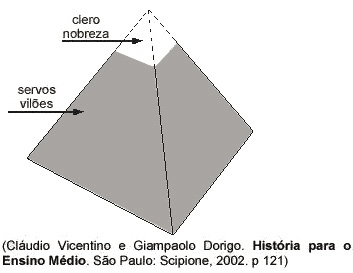
A sociedade feudal pode ser representada por uma pirâmide regular de volume 500cm3 e altura igual a 10cm. Se o “clero e a nobreza” correspondem a uma outra pirâmide regular de altura 1cm, como mostra a figura, então o volume, em centímetros cúbicos, dessa outra pirâmide é:
a) 0,02
b) 0,50
c) 2
d) 1
e) 10
Questão 04
Um telhado tem a forma da superfície lateral de uma pirâmide regular, de base quadrada. O lado da base mede 8m e a altura da pirâmide 3m. As telhas para cobrir esse telhado são vendidas em lotes que cobrem 1m2. Supondo que possa haver 10 lotes de telhas desperdiçadas (quebras e emendas), o número mínimo de lotes de telhas a ser comprado é:
a) 90
b) 100
c) 110
d) 120
e) 130
Dica 3 – Relembre tudo sobre Ângulos na Circunferência em mais esta aula preparatória para a prova de Matemática Enem. Estude com a gente, o Enem está chegando! – https://blogdoenem.com.br/angulos-na-circunferencia-matematica-enem/
Questão 05
Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19cm de altura e 6cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior , espaçados de 1cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
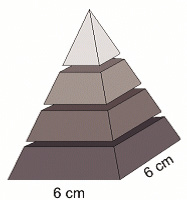
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
a) 156cm3.
b) 189cm3.
c) 192cm3.
d) 216cm3.
e) 540cm3.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
