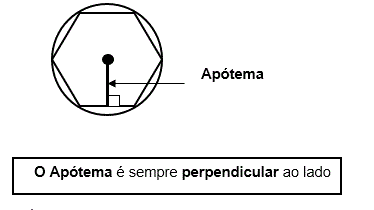
Apótema é o segmento de reta que parte do centro de um polígono regular e forma um ângulo de 90º com a sua lateral. Para calcular o valor do apótema de um triângulo, quadrado ou hexágono é preciso circunscrever o polígono a uma circunferência. Veja!
Os cálculos que envolvem polígonos regulares estão presentes no Enem, nos vestibulares e no Encceja. Você já deve conhecer os principais elementos das figuras planas, que são os vértices, arestas, ângulos e diagonais.
Mas os polígonos regulares também possuem outro elemento chamado apótema. Nesta aula você vai ver o que é inscrição e circunscrição de polígonos, vai conhecer a definição de apótema e aprender a calcular o seu valor.
Polígonos regulares
Para que você entenda o que é apótema, é preciso saber o que é um polígono regular e também que ele pode ser inscrito ou circunscrito em uma circunferência. Primeiramente, vamos à definição: polígono regular é aquele que tem todos os lados e ângulos congruentes.
Ou seja: todos os lados tem o mesmo valor e todos os ângulos internos também possuem o mesmo valor. Observe os exemplos: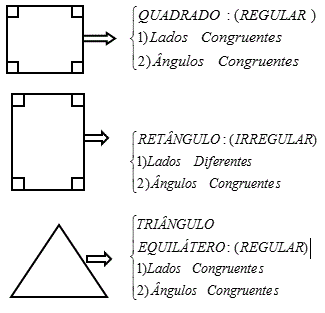
Polígono regular inscrito e circunscrito
Já vimos que o polígono regular tem os lados iguais e os ângulos também iguais. Em seguida vamos entender o que é inscrição e circunscrição de polígonos.
Polígono inscrito
O polígono inscrito na circunferência é o aquele cujos vértices ficam dentro da circunferência. Também podemos dizer que a circunferência está circunscrito ao polígono. Por fim, é importante lembrar que as arestas da figura são as cordas da circunferência.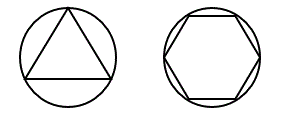
Polígono circunscrito
Enquanto isso, polígono circunscrito à circunferência é aquele cujos lados são tangentes à circunferência. Também podemos dizer que a circunferência está inscrita ao polígono.
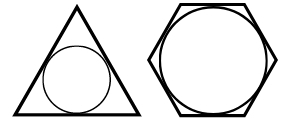
O cálculo do apótema
Apótema é o segmento de reta que parte do centro de um polígono e forma um ângulo de 90º com a sua lateral. Dessa maneira, podemos dizer que o apótema é perpendicular ao lado do polígono.
Veja na figura abaixo que o segmento em verde do hexágono é o apótema do mesmo. Ele se origina a partir do centro do hexágono e termina tocando um de seus lados: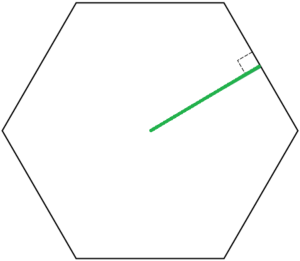
Outra possibilidade de definição de apótema é o raio da circunferência inscrita em um polígono. Para que você entenda melhor, pense na circunferência e no seu raio.
O raio é a medida do centro da circunferência até um ponto qualquer na mesma. Pois bem, com o apótema podemos pensar quase o mesmo, com a diferença de que ele não é a medida de um ponto qualquer do polígono, mas sim a medida de seu centro até um de seus lados.
Veja agora com o professor Lucas Borguezan, do canal do Curso Enem Gratuito, como fazer o Cálculo do Apótema em Polígonos:
Em seguida, você pode ver a figura de um quadrado, de um hexágono e de um triângulo com circunferências inscritas. Observe em seguida que a linha vermelha é tanto o raio da circunferência quanto o apótema dos polígonos.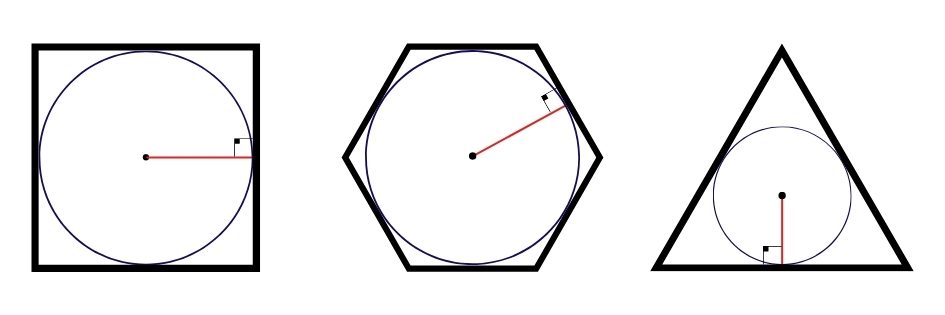
Generalidades dos Polígonos na Geometria Plana:
- O centro de um polígono regular é o centro da circunferência circunscrita;
- O apótema de um polígono regular é o raio da circunferência circunscrita;
- Apótema de um polígono regular é a distância do centro a qualquer lado, desde que forme um ângulo de 90º.

Resumo sobre os Poligonos
Veja um resumo simples e rápido com o professor Sérgio Sarkis do canal Curso Enem Gratuito e em seguida confira o conteúdo sobre apótema:
Para que serve o apótema
O apótema é muito útil na geometria plana e na geometria espacial. Com ele você pode calcular o raio de uma circunferência inscrita num polígono regular e calcular a distância de um dos lados do polígono até seu centro. Além disso, você pode descobrir a distância entre um ponto médio de uma corda até o centro de sua circunferência.
Como calcular o apótema do Triângulo
Em seguida você pode conferir um resumo com os principais polígonos regulares e suas respectivas fórmulas para calcular o apótema, a área, o perímetro e o raio.
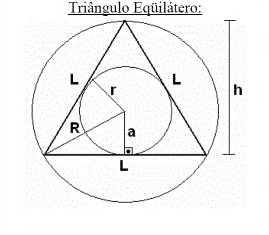
- Área: A = (L².√3)/4 ou A = (3.L)/2 . a
- Perímetro: P = 3.L
- Altura: h = (L.√3)/2
- Apótema: a = (L.√3)/6 = R/2
- Raio da circunferência inscrita: r = (L.√3)/6
- Raio da circunferência circunscrita: R = (L.√3)/3
Apótema do quadrado
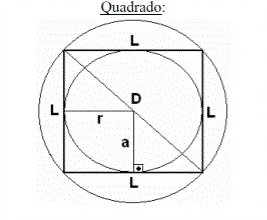
- Área: A = L² ou A = 2.L.a
- Perímetro: P = 4.L
- Diagonal: D = L.√2
- Apótema: a = L/2
- Raio da circunferência inscrita: r = L/2
- Raio da circunferência circunscrita: R = D/2 = L.√2/2
Apótema do hexágono
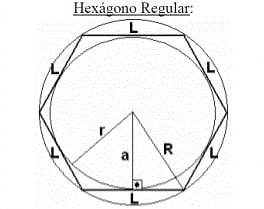
- Área: A= (6.L².√3)/4 = (3L²√3)/2 ou A = 3 .L.a
- Perímetro: P = 6.L
- Apótema: a = (L√3)/2
- Raio da circunferência inscrita: r = (L√3)/2
- Raio da circunferência circunscrita: R = L
Exercícios sobre apótema
1 – (UECE/2016)
A razão entre as áreas de um triângulo equilátero inscrito em uma circunferência e a área de um hexágono regular cuja medida do apótema é 10 m circunscrito à mesma circunferência é
a) 3/8.
b) 5/8.
c) 3/7.
d) 5/7.
2 – (UECE/2019)
Em um plano, considere um círculo cuja medida do raio é igual a 0,5 m, um quadrado Q circunscrito ao círculo e um quadrado q inscrito no mesmo círculo. Podemos afirmar corretamente que a medida, em m2, da área da região do plano interior a Q e exterior a q é
a) 0,15π.
b) 0,25π.
c) 0,50.
d) 0,35.
3 – (UNIRG TO/2012)
Em uma determinada construção o engenheiro responsável dá um problema de cálculo de área de uma estrutura para ser resolvido por seu estagiário. A estrutura é representada na figura a seguir. O problema consiste em determinar o lado do quadrado. Este quadrado está circunscrito por uma circunferência cuja medida da área é 7.500 m2.

Sabendo-se que os lados do quadrado tangenciam a circunferência, e que o estagiário resolveu corretamente o problema. Então, o valor do lado do quadrado é:
(considere π = 3)
a) 25 m
b) 50 m
c) 75 m
d) 100 m
4- (FRANCO)
O lado do quadrado inscrito numa circunferência mede 4 cm. O lado do triângulo equilátero inscrito na mesma circunferência mede:
a) 2√3
b) 2√6
c) 3√2
d) 6√2
5- (FRANCO)
O perímetro de um quadrado inscrito numa circunferência cujo apótema mede 3(1/2) cm é:
a) 24 cm
b) 26 cm
c) 28 cm
d) 30 cm
GABARITO:
- A
- C
- D
- B
- C