Você conhece o círculo trigonométrico? Não? Então veja esta super aula do professor Lucas Borghesan, do Curso Enem Gratuito, que é pra você gabaritar Seno e Cosseno no Enem.
O tema desta aula de Matemática Enem aborda um grande aliado para você se dar bem no concurso: o círculo trigonométrico – representação trigonométrica muito importante das funções seno, cosseno e tangente para resolver diversos problemas envolvendo trigonometria.
Existem algumas unidades conhecidas com as quais podemos medir um ângulo. A mais conhecida é o grau, mas há também o radiano. Venha estudar os ângulos na circunferência e se garanta em trigonometria para o Enem! Confira as Unidades de Medida.
Unidades de medidas de ângulos
- Grau: Dividindo uma circunferência em 360 partes iguais, ligamos o centro a cada um desses pontos marcados nessa circunferência. Com essa operação conseguimos determinar 360 ângulos centrais. Cada um desses ângulos é chamado de 1 grau.
- Radiano: Outra unidade é chamada de radiano. Essa é uma das mais importantes e é a que mais faremos uso no nosso curso de trigonometria.
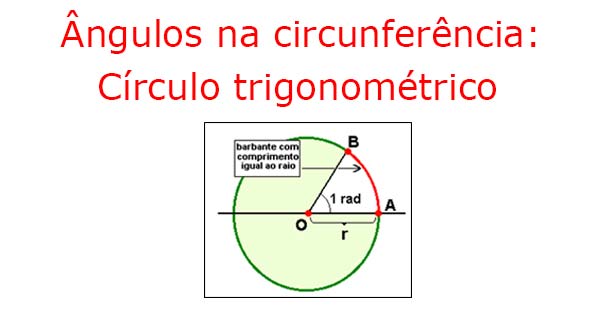
Veja no exemplo da Formiguinha, como é simples:
Sejamos práticos, para aprender agora:
- Desenhe no chão uma circunferência de raio r.
- Agora, faça uma formiga andar sobre essa circunferência (sobre a curva) o equivalente à r.
- Marque o lugar que ela pára.
- Agora, marque o ângulo central que corresponde à esse arco que a formiga andou.
- Esse ângulo central formado mede 1 radiano (1 rd).
Os ângulos na circunferência
Para começar bem o seu resumo sobre os ângulos na circunferência acompanhe esta introdução completa com o professor Lucas Borguesan, do canal do Curso Enem Gratuito. Veja a Aula parte 1; e depois o complemento.:
As dicas do Professor Lucas. Parte 1:
- Podemos dizer que todo polígono regular pode ser inscrito ou circunscrito a uma circunferência. Isso quer dizer que em todo polígono regular podemos “desenhar” uma circunferência no seu interior e no seu exterior.
- Caso a circunferência esteja no interior do polígono, dizemos que a circunferência está inscrita ao polígono ou que o polígono está circunscrito à circunferência.
- Por outro lado, caso a circunferência esteja no exterior do polígono, dizemos que a circunferência está circunscrita ao polígono ou que o polígono está inscrito à circunferência.
- Nesta aula acima, o professor Lucas vai te introduzir nos cálculos de ângulos da circunferência.
Os Ângulos na Circunferência, parte 2:
- Parabéns, você completou o resumo dos ângulos.
- Agora, o desafio é como utilizar o Círculo Trigonométrico para gabaritar no Enem.
- Veja a seguir:
O Círculo Trigonométrico
Aprenda agora na aula bem didática do professor Lucas Borguesan, do canal do Curso Enem Gratuito, para você dominar de maneira prática os segredos do Círculo Trigonométrico:
As dicas sobre o Círculo Trigonométrico:
- O ciclo trigonométrico é um círculo de raio 1. Ou seja, do seu cento até a borda, a medida é 1.
- Assim, podemos definir todos os valores de seno e cosseno que existem, uma vez que o círculo trigonométrico compreende todos os ângulos.
- Na trigonometria, seno e cosseno são chamados de razões trigonométricas.
- Para medir o valor do seno, é comum usar o eixo vertical do círculo trigonométrico. Desta forma, o eixo vertical do ciclo trigonométrico é chamado eixo dos senos.
- Por outro lado, podemos encontrar o valor do cosseno no eixo horizontal, de maneira que este é chamado de eixo dos cossenos.
- Veja no resumo abaixo, para você dominar e mandar bem no Enem.
.
. Aprenda agora a fazer as conversões trigonométicas
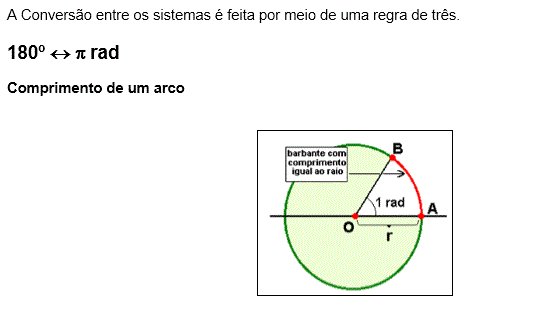
Círculo Trigonométrico ou Ciclo Trigonométrico
A circunferência trigonométrica ou ciclo trigonométrico é de extrema importância para o nosso estudo da Trigonometria, pois é baseado nela que todos os teoremas serão deduzidos.
Trata-se de uma circunferência com centro na origem do sistema de eixos coordenados e de raio 1, como é mostrado na figura abaixo:
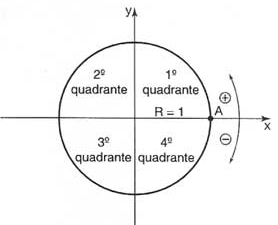
Os eixos dividem a circunferência em 4 partes iguais denominados quadrantes.
Convenciona-se que o sentido anti-horário é o sentido positivo na circunferência trigonométrica.
Expressão geral dos arcos
Imagine a seguinte situação: estamos caminhando sobre uma pista circular, logo, sairemos de um marco zero e vamos prosseguindo de tal forma que num determinado momento chegamos ao mesmo ponto de partida.

Para finalizar sua revisão, clique no link abaixo e assista a videoaula do canal RedeXplica, do Youtube: