Aprenda Cálculo de Porcentagem: resumo de Matemática Enem

 Aprenda cálculo de porcentagem:

Veja nos detalhes, como entender e resolver Cálculo de Porcentagem:

É qualquer razão (fração) cujo denominador seja  igual a 100. Por exemplo: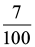 

Você pode ler “sete sobre cem”, o que significa sete partes das cem partes disponíveis.  E uma porcentagem, e pode ser lida como “sete por cento” quando colocamos o símbolo da porcentagem ao lado do número sete, eliminando a necessidade de apresentar a fração.

Costumamos usar o símbolo % da seguinte maneira: 7%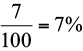

Aula Gratuita de Cálculo de Porcentagem

Veja com o professor Sérgio Sarkis, do Curso Enem Gratuito, uma aula completa para você aprender de vez como fazer o Cálculo de Porcentagem, e depois siga com mais exemplos e um simulado também.

O que mais ocorre, no entanto, são porcentagens sobre outros números, como 30% de 90 ou 80% de 40, por exemplo. Vamos ver o que isso significa.

Exemplo 01:   30% de 20 significa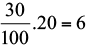 

Exemplo 02:   40% de 70 significa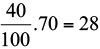 

Exemplo 03: 24% de 30 significa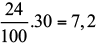 

Exemplo 04 – Um comerciante remarca um produto com um aumento de 20%. Agora o novo preço equivale a multiplicar o anterior por quanto?. Veja a Resolução:

Se o produto custa x, então 20% de x se calcula assim: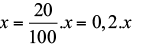 

Com o aumento, o novo preço equivale a  P = x + 0,2x ⇒ P = 1,2.x

.

Dica do Blog: Este é um fato que pode ser generalizado. Se aplicarmos um aumento de 30%, o novo valor passa a ser multiplicado por 1,3; aumentando 3%, o novo valor será multiplicado por 1,03, e assim por diante.

Dica 1 – Você lembra como funcionam a Regra de Três Simples e a Regra de Três Composta? Revise com esta aula de Razões e Proporções para a prova de Matemática Enem – https://blogdoenem.com.br/razoes-e-proporcoes-matematica-enem/ 

Aula Gratuita de Regra de Três – Sempre cai

Confira com o professor Vinny, do canal Curso Enem Gratuito, como resolver Regra de Três de maneira simples e rápida.

. Gostou do Resumo? Muito Bom!

Exemplo 05 de Cálculo de Porcentagem – Um comerciante remarca um produto com um desconto de 20%. Agora o novo preço equivale a multiplicar o anterior por quanto?

Resolução:   Se o produto custa x, então 20% de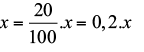 

Com o desconto, o novo preço equivale a   P = x + 0,2x ⇒ P = 0,8.x

Dica do Blog: Este é um fato que pode ser generalizado. Ao aplicar um desconto de 30%, o novo valor passa a ser multiplicado por 0,7; descontando 3%, o novo valor será multiplicado por 0,97, e assim por diante.

Dica 2 –  Você já sabe tudo sobre polinômios? Nesta aula de Matemática Enem vamos aprender Adição, Subtração, Multiplicação e Divisão polinomial – https://blogdoenem.com.br/definicoes-propriedades-dos-polinomios-matematica-enem/

Exemplo 06 – Um produto foi aumentado em 30%, passando a custar R$ 78,00. Qual o preço do produto antes do aumento? – Veja a Resolução:

Se o produto foi aumentado em 30%, então o valor R$ 78,00 representa agora 130% do produto, assim, por regra de três:

%              valor

130              78

100               x

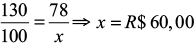
Simulado de cálculo de Porcentagem

Teste o seu nível agora respondendo a 10 questões sobre o Cálculo de Porcentagem. O Gabarito sai na hora. Vem para o Simulado Enem de Porcentagem:

Veja mais Exercícios de aplicação sobre o Cálculo de Porcentagem

Exercício 01 Aprenda Cálculo de Porcentagem

(ENEM cancelado, 2009) Considere que as médias finais dos alunos de um curso foram representadas no gráfico a seguir.

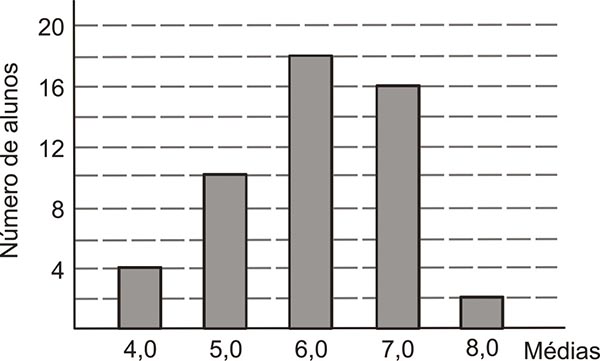
Sabendo que a média para aprovação nesse curso era maior ou igual a 6,0, qual foi a porcentagem de alunos aprovados?

a) 18%

b) 21%

c) 36%

d) 50%

e) 72%

Exercício 02

(ENEM, 2010) O jornal de certa cidade publicou em uma página inteira a seguinte divulgação de seu caderno de classificados:

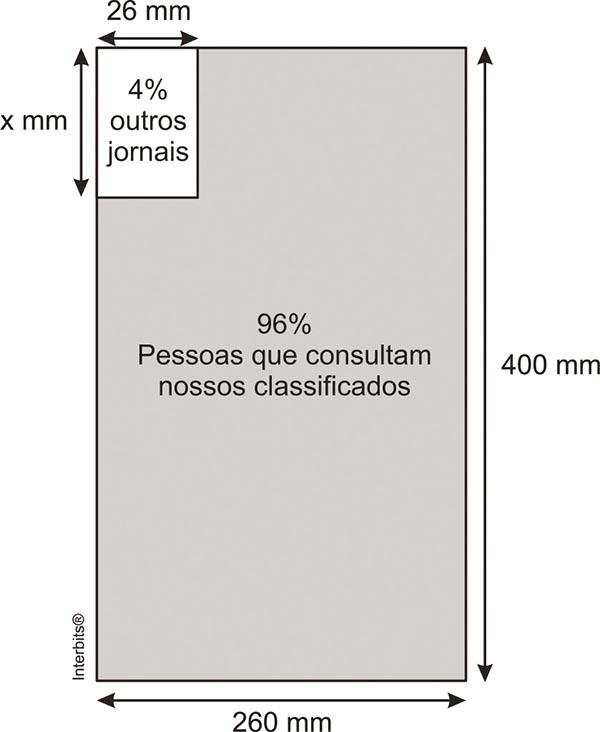
Para que a propaganda seja fidedigna, a porcentagem da área que aparece na divulgação, a medida do lado do retângulo que representa os 4%, deve ser aproximadamente de:

a) 1 mm

b) 10 mm

c) 17 mm

d) 160 mm

e) 167 mm

Dica 3 – Que tal revisar Funções Polinomiais? Confira exercícios resolvidos nesta aula de Matemática Enem para lhe ajudar a fixar o conteúdo – https://blogdoenem.com.br/funcoes-polinomiais-matematica-enem/

Exercício 03

(MACK) Nos três primeiros meses do ano a inflação foi de 5, 4 e 6%. Qual a inflação acumulada no trimestre?

Gabarito: 15,75%

Desafios sobre o Cálculo de Porcentagem

Questão 01

(ENEM, 2010) Os dados do gráfico foram coletados por meio da Pesquisa Nacional por Amostra de Domicílios.

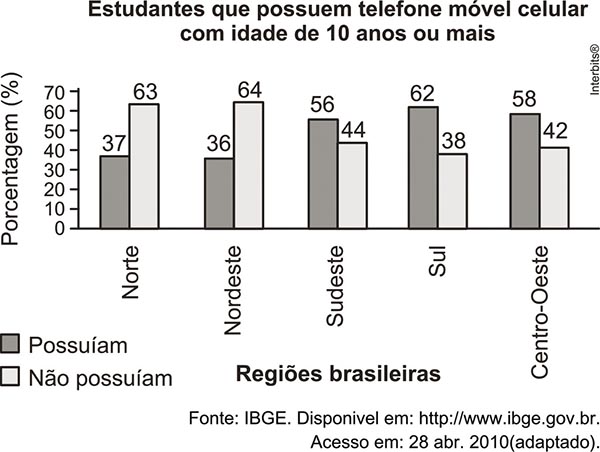
Supondo-se que, no Sudeste, 14.900 estudantes foram entrevistados nessa pesquisa, quantos deles possuíam telefone móvel celular?

a) 5.513

b) 6.556

c) 7.450

d) 8.344

e) 9.536

Questão 02

(ENEM, 2004) As “margarinas” e os chamados “cremes vegetais” são produtos diferentes, comercializados em embalagens quase idênticas. O consumidor, para diferenciar um produto do outro, deve ler com atenção os dizeres do rótulo, geralmente em letras muito pequenas. As figuras que seguem representam rótulos desses dois produtos.

Uma função dos lipídios no preparo das massas alimentícias é torná-las mais macias. Uma pessoa que, por desatenção, use 200 g de creme vegetal para preparar uma massa cuja receita pede 200 g de margarina, não obterá a consistência desejada, pois estará utilizando uma quantidade de lipídios que é, em relação à recomendada, aproximadamente:

a) O triplo.

b) O dobro.

c) A metade.

d) Um terço.

e) Um quarto.

Questão 03

(ENEM, 2001) Nas últimas eleições presidenciais de um determinado país, onde 9% dos eleitores votaram em branco e 11% anularam o voto, o vencedor obteve 51% dos votos válidos. Não são considerados válidos os votos em branco e nulos.

Pode-se afirmar que o vencedor, de fato, obteve de todos os eleitores um percentual de votos da ordem de

a) 38%

b) 41%

c) 44%

d) 47%

e) 50%

Questão 04

(ENEM, 2011) Um jovem investidor precisa escolher qual investimento lhe trará maior retomo financeiro em uma aplicação de R$ 500,00. Para isso, pesquisa o rendimento e o imposto a ser pago em dois investimentos: poupança e CDB (certificado de depósito bancário). As informações obtidas estão resumidas no quadro:

Para o jovem investidor, ao final de um mês, a aplicação mais vantajosa é

a) A poupança, pois totalizará um montante de R$ 502,80.

b) A poupança, pois totalizará um montante de R$ 500,56.

c) O CDB, pois totalizará um montante de R$ 504,38.

d) O CDB, pois totalizará um montante de R$ 504,21.

e) O CDB, pois totalizará um montante de R$ 500,87.

Questão 05

(ENEM, 2011) Uma pessoa aplicou certa quantia em ações. No primeiro mês, ela perdeu 30% do total do investimento e, no segundo mês, recuperou 20% do que havia perdido.

Depois desses dois meses, resolveu tirar o montante de R$ 3.800,00 gerado pela aplicação.

A quantia inicial que essa pessoa aplicou em ações corresponde ao valor de:

a) R$ 4.222, 22

b) R$ 4.523,80

c) R$ 5.000,00

d) R$ 13.300,00

e) R$ 17.100,00