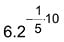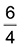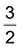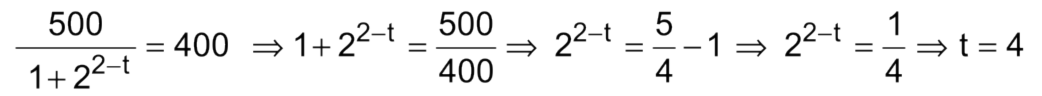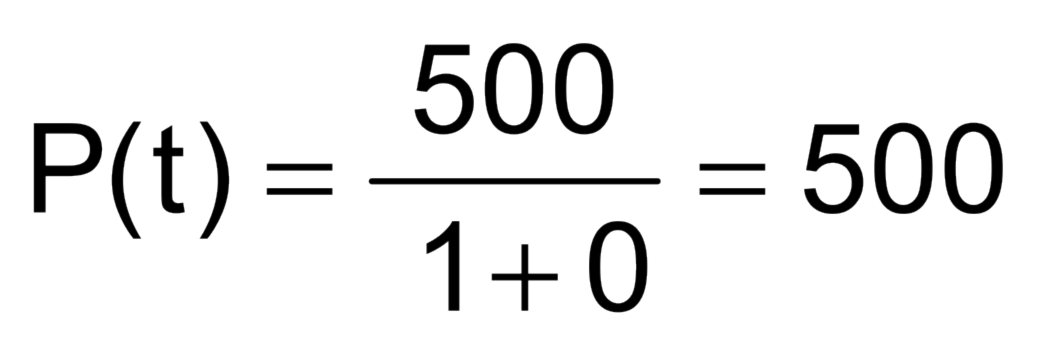Acertar uma questão de Equações Exponenciais faz toda a diferença para garantir uma boa nota na prova de Matemática do Enem ou no Vestibular. Você lembra direitinho? Ainda não? - Então veja abaixo uma revisão com exercícios resolvidos e desafios para você!
Você domina os cálculos de Matemática para resolver Equações Exponenciais? – Acerte uma questão dessas para disprar na frente da concorrência. Você lembra o que é uma Equação exponencial? Vamos lá, então, com o resumo e exercícios resolvidos sobre as Equações Exponenciais.
Chama-se equação exponencial toda equação que pode ser reduzida a forma ax = b, com 0 < a 1. Para resolver tais equações é necessário transformar a equação dada em: Igualdade de potência de mesma base: af(x)= ag(x) → f(x) = g(x); e, ainda com Potências de expoentes iguais: af(x) = bf(x) → a = b, sendo a e b ≠ 1 e a e b ∈ R*+
Mas, dominar a definição não adianta. O que vale ponto , mesmo, é resolver as questões do Enem, do Encceja e dos Vestibulares. Veja um resumo simples e rápido com o professor Sérgio Sarkis, do canal Curso Enem Gratuito, e depois vamos aos exercícios resolvidos.
Aula Gratuita: Como resolver Equações Exponenciais
Muito bom este resumo! Agora, vamos avançar, para um exercício resolvido, que ajuda você a lembrar os conteúdos e o modo de resolução. Confira a seguir:
Exercício resolvido de Equação Exponencial:
(UEL – 2012) A espessura da camada de creme formada sobre um café expresso na xícara, servido na cafeteria A, no decorrer do tempo, é descrita pela função E(t) = a2bt, onde t ≥ 0 é o tempo (em segundos) e a e b são números reais. Sabendo que inicialmente a espessura do creme é de 6 milímetros e que, depois de 5 segundos, se reduziu em 50%, qual a espessura depois de 10 segundos?
- Vamos lá:
- E(0) = 6
- 6 = a ⋅2b ⋅0 ⇔ 6 = a ⋅1 ⇔ a = 6
- E(5) = 0,5 ⋅ 6 = 3
- Portanto, E(t) =
. - Calculando E(10), tem-se:
- E(10) =
- E(10) = 6.2-2
- E(10) =
- E(10) =
- Resposta: 1,5 mm
.
Dica do Blog do Enem: O que mais cai de Matemática
Veja a relação dos conteúdos de matemática que mais caem nas provas do Enem e nos vestibulares mais puxados. A lista foi elaborada pelo professor Carlos Oliveira, do Colégio Bandeirantes, de São Paulo: 
Confira na imagem acima a relação dos Temas top ten da Matemática do Enem, com aulas gratuitas.
Agora, veja uma nova abordagem de Função Exponencial:
- Chama-se função exponencial toda função que pode ser reduzida à forma:
- f(x) = ax + b,a > 0 e a ≠ 1
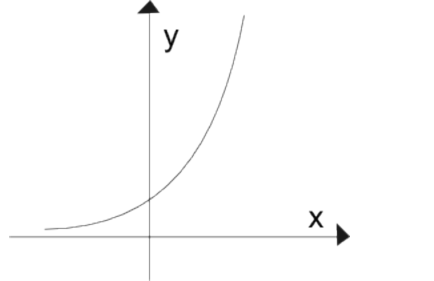
- Veja nos Gráficos: Para a > 1, a função é crescente:
- Para 0 < a < 1, a função é decrescente:
Imagem da função:
Para a função f(x)= ax + b a sua imagem será Im = [b,∞].
Exercício resolvido sobre função exponencial:
(UFPR, 2012) – Um grupo de cientistas decidiu utilizar o seguinte modelo logístico, bastante conhecido por matemáticos e biólogos, para estimar o número de pássaros, P(t), de determinada espécie numa área de proteção ambiental. Sendo t o tempo em anos e t = 0 o momento em que o estudo foi iniciado.
- a) Em quanto tempo a população chegará a 400 indivíduos?
- Resolução:
- b) À medida que o tempo t aumenta, o número de pássaros dessa espécie se aproxima de qual valor? Justifique sua resposta.
- Resolução: Para t muito grande, o valor 22-t tende a ser 0; logo, P(t) será dado por
- Portanto, o número de pássaros dessa espécie se aproxima a 500.
Exercícios sobre Equações Exponenciais:
Desafios com Equações Exponenciais para você resolver e compartilhar a resposta:
Questão 1 – (MACKENZIE, 2010) O valor de x na equação
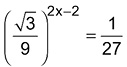é:
a) Tal que 2 < x < 3 b) Negativo c) Tal que 0 < x < 1 d) Múltiplo de 2 e) 3
Questão 2 – (UFJF, 2006) Dada a equação 23x-2 ⋅ 8x+1 = 4x-1 , pode-se afirmar que sua solução é um número:
a) Natural b) Maior que 1 c) De módulo maior que 1 d) Par e) De módulo menor que 1
Dica 2 – Relembre sobre as Equações Racionais e Irracionais em mais esta aula de revisão para a prova de Matemática Enem – https://blogdoenem.com.br/equacoes-racionais-irracionais-matematica-enem/
Questão 3 – (G1 – CFTMG, 2005) A solução da equação 3x+1 -3x+2=-54 é:
a) – 2 b) – 1 c) 0 d) 2
Dicas de Matemática do Blog do Enem. Potencialização e Radiciação, e Polinômios. Confira:
1 – Revise aqui sobre Potencialização e Radiciação em mais esta aula de Matemática Enem.
2 – Relembre aqui as funções e propriedades dos Polinômios nesta aula de revisão para Matemática Enem.
Questão 4 – (UERJ, 1999) Pelos programas de controle de tuberculose, sabe-se que o risco de infecção R depende do tempo t, em anos, do seguinte modo: R=R0 e-yt, em que R0 é o risco de infecção no início da contagem do tempo t, e y é o coeficiente de declínio.
O risco de infecção atual em Salvador foi estimado em 2%. Suponha que, com a implantação de um programa nesta cidade, fosse obtida uma redução no risco de 10% ao ano, isto é, y=10%.
Use a tabela abaixo para os cálculos necessários:
| ex | 8,2 | 9,0 | 10,0 | 11,0 | 12,2 |
| x | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 |
O tempo, em anos, para que o risco de infecção se torne igual a 0,2%, é de:
a) 21 b) 22 c) 23 d) 24
Questão 5 – Equações Exponenciais – (FUVEST-GV, 1991) Dado o sistema
,
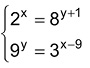pode-se dizer que x + y é igual a:
a) 18 b) – 21 c) 27 d) 3 e) – 9
Você consegue resolver estes exercícios de Equações Exponenciais? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
