Relembre como resolver exercícios sobre média aritmética simples e ponderada e teste o que aprendeu com questões de Matemática do Enem e dos vestibulares!
Média aritmética é um conteúdo relativamente fácil e que você não pode deixar de fora dos seus estudos porque sempre cai no Enem. Por isso, selecionamos uma série de exercícios sobre média aritmética simples e ponderada para você praticar para a prova e testar seus conhecimentos.
Resumo sobre média aritmética
Antes de partir para os exercícios sobre média aritmética, vamos ver como calcular a média simples e a média ponderada.
A média aritmética simples também é conhecida apenas por média. É a medida de posição mais utilizada e a mais intuitiva de todas. Ela está tão presente em nosso dia-a-dia que qualquer pessoa entende seu significado e a utiliza com frequência.
Assim, a média aritmética de um conjunto de valores numéricos é calculada somando-se todos esses valores e dividindo-se o resultado pelo número de elementos somados, que é igual ao número de elementos do conjunto. Ou seja, a média de n números é sua soma dividida por n.
Considere a seguinte situação: a lista abaixo mostra as notas de matemática de um aluno em um determinado ano. Qual será sua média final?
- 1º bimestre: 3,5
- 2º bimestre: 7,5
- 3º bimestre: 9,0
- 4º bimestre: 6,0
Para calcular a média aritmética, somamos as notas de todos os bimestres e dividimos por 4:
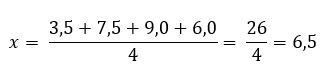
Portanto, a média do aluno foi de 6,5. Isso significa dizer que, apesar de ele ter obtido notas mais altas ou mais baixas em outros bimestres, a soma das notas (26) é a mesma que ele alcançaria se tivesse obtido nota 6,5 em todos os bimestres.
Média aritmética ponderada
Nos cálculos envolvendo média aritmética simples, todas as ocorrências têm exatamente a mesma importância ou o mesmo peso. Dizemos então que elas têm o mesmo peso relativo. No entanto, existem casos em que as ocorrências têm importância relativa diferente.
Nesses casos, o cálculo da média deve levar em conta a importância relativa ou peso relativo. Este tipo de média chama-se média ponderada. No cálculo da média ponderada, multiplicamos cada valor do conjunto por seu “peso”, isto é, sua importância relativa.
Considere a seguinte situação: 5 baldes contêm 4 litros de água cada um, 3 outros possuem 2 litros de água cada um e, ainda, 2 outros contêm 5 litros de água cada um. Se toda essa água fosse distribuída igualmente em cada um dos baldes, com quantos litros ficaria cada um?
Para solucionarmos esse exercício, precisamos calcular a média ponderada. Para isso, multiplicamos a quantidade de água pela quantidade de balde e somamos o resultado. Em seguida, dividimos o valor obtido pela quantidade de baldes:
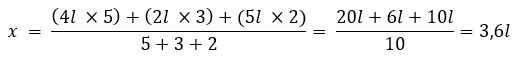
Ou seja, a quantidade, em litros, de água em cada balde é chamada de média ponderada dos valores 4 litros, 2 litros e 5 litros, com pesos 5, 3 e 2.
Exemplo de média aritmética simples e ponderada
As médias escolares podem ser calculadas por meio das médias simples. Suponha que para passar de ano você precisa tirar média 7 e a média é calculada com 4 provas. A fim de obter sua média, precisaremos pegar as notas que você tirou em todas as provas e dividir por 4. Imagine que na primeira prova você tirou 8, na segunda tirou 7, na outra tirou 6 e na última tirou 7. Partimos, então, para o cálculo:
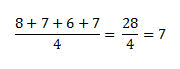
Sua média, neste caso, seria 7 e você estaria aprovado.
Usando o mesmo exemplo da nota escolar, imagine que cada uma das notas tem um peso distinto. A primeira e a segunda provas possuíam peso 2, e a terceira e a quarta possuíam peso 3. Como podemos fazer esse cálculo? Multiplica-se o valor pelo seu peso, somando aos resultados das outras multiplicações e então divide-se pela soma de todos os pesos. Confira o cálculo do exemplo:
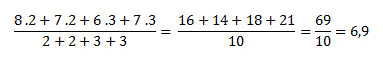
Nesse caso, a média seria 6,9.
Na média ponderada, ao contrário da média simples, a alteração da posição dos números pode ocasionar em resultados errados. Se você errasse, por exemplo, aplicando peso 1 às duas primeiras notas e peso 2 às seguintes, sua média seria diferente:
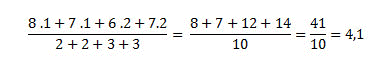
Videoaula
Para reforçar sua revisão, assista à aula do professor Sarkis e, em seguida, resolva os exercícios sobre média aritmética!
Exercícios sobre média aritmética
Saiba como este conteúdo aparece no Enem e nos vestibulares:
Sumário do Quiz
0 de 10 questões completadas
Perguntas:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
Information
.
Você já fez este questionário anteriormente. Portanto, não pode fazê-lo novamente.
Quiz is loading...
You must sign in or sign up to start the quiz.
Para iniciar este questionário, você precisa terminar, antes, este questionário:
Resultados
0 de 10 perguntas respondidas corretamente
Seu tempo:
Acabou o tempo
Você conseguiu 0 de 0 pontos possíveis (0)
| Pontuação média |
|
| Sua pontuação |
|
Categorias
- Sem categoria 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- Respondido
- Revisão
-
Pergunta 1 de 10
1. Pergunta
(IFSC/2017)
Segundo dados do IBGE (Instituto Brasileiro de Geografia e Estatística), o rendimento médio mensal das famílias catarinenses é R$ 1368,00.
Considerando-se que uma família pegou um empréstimo no valor de 30% de sua renda média mensal e vai pagar este empréstimo a uma taxa de juros compostos de 2% ao mês, responda:A) Quanto essa família pegou emprestado?
B) Qual o valor que a família irá pagar (montante final) se saldar essa dívida em 2 meses?Assinale a alternativa CORRETA, que contém as respostas das questões acima.
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 2 de 10
2. Pergunta
(IFSC/2017)
O Instituto Brasileiro de Geografia e Estatística (IBGE) divulgou, em 15/03/2016, a taxa de desemprego do país que teve a piora mais acelerada registrada nesses quatro anos da série histórica da pesquisa de emprego do IBGE. Essa taxa cresceu para 8,5% na média do ano passado, a maior já medida pela Pesquisa Nacional por Amostra de Domicílios (Pnad), iniciada em 2012.
Sabendo-se que, em 2014, a taxa de desemprego média era de 6,8%, é CORRETO afirmar que o crescimento percentual na taxa de desemprego do ano de 2014 para 2015 foi de aproximadamente
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 3 de 10
3. Pergunta
(ENEM/2016)
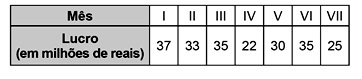
Preocupada com seus resultados, uma empresa fez um balanço dos lucros obtidos nos últimos sete meses, conforme dados do quadro.

Avaliando os resultados, o conselho diretor da empresa decidiu comprar, nos dois meses subsequentes, a mesma quantidade de matéria-prima comprada no mês em que o lucro mais se aproximou da média dos lucros mensais dessa empresa nesse período de sete meses.
Nos próximos dois meses, essa empresa deverá comprar a mesma quantidade de matéria-prima comprada no mês
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 4 de 10
4. Pergunta
(ENEM/2016)
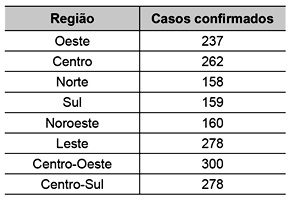
Em uma cidade, o número de casos de dengue confirmados aumentou consideravelmente nos últimos dias. A prefeitura resolveu desenvolver uma ação contratando funcionários para ajudar no combate à doença, os quais orientarão os moradores a eliminarem criadouros do mosquito Aedes aegypti, transmissor da dengue. A tabela apresenta o número atual de casos confirmados, por região da cidade.

A prefeitura optou pela seguinte distribuição dos funcionários a serem contratados:I. 10 funcionários para cada região da cidade cujo número de casos seja maior que a média dos casos confirmados.
II. 7 funcionários para cada região da cidade cujo número de casos seja menor ou igual à média dos casos confirmados.Quantos funcionários a prefeitura deverá contratar para efetivar a ação?
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 5 de 10
5. Pergunta
(UNCISAL/2016)
Um professor prometeu um churrasco para sua turma de 20 alunos se a média aritmética das notas finais da turma fosse superior ou igual a 7,50. O planejamento da disciplina previa a realização de três avaliações (um trabalho individual, um trabalho em grupo e uma prova, realizadas nesta ordem) e a nota final de cada aluno seria a média ponderada dessas avaliações, com pesos 2, 3 e 5, respectivamente. Mesmo levando em conta que Joana (7,00 no trabalho individual e 5,00 no trabalho em grupo) não compareceu à prova por motivo de doença, o professor verificou que a média dos outros dezenove alunos foi igual a 7,60. Que nota mínima Joana precisa obter na segunda chamada para a turma ganhar o churrasco?
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 6 de 10
6. Pergunta
(ENEM/2017)
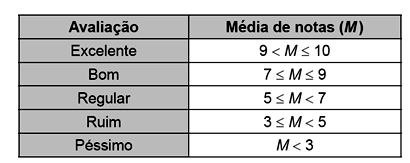
A avaliação de rendimento de alunos de um curso universitário baseia-se na média ponderada das notas obtidas nas disciplinas pelos respectivos números de créditos, como mostra o quadro:

Quanto melhor a avaliação de um aluno em determinado período letivo, maior sua prioridade na escolha de disciplinas para o período seguinte.
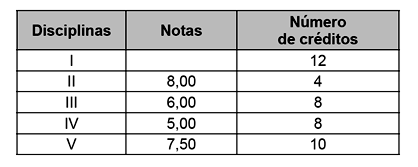
Determinado aluno sabe que se obtiver avaliação “Bom” ou “Excelente” conseguirá matrícula nas disciplinas que deseja. Ele já realizou as provas de 4 das 5 disciplinas em que está matriculado, mas ainda não realizou a prova da disciplina I, conforme o quadro.

Para que atinja seu objetivo, a nota mínima que ele deve conseguir na disciplina I é
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 7 de 10
7. Pergunta
(ENEM/2014)
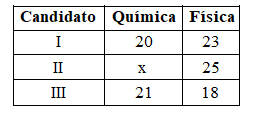
Ao final de uma competição de ciências em uma escola, restaram apenas três candidatos. De acordo com as regras, o vencedor será o candidato que obtiver a maior média ponderada entre as notas das provas finais nas disciplinas química e física, considerando, respectivamente, os pesos 4 e 6 para elas. As notas são sempre números inteiros. Por questões médicas, o candidato II ainda não fez a prova final de química. No dia em que sua avaliação for aplicada, as notas dos outros dois candidatos, em ambas as disciplinas, já terão sido divulgadas.
O quadro apresenta as notas obtidas pelos finalistas nas provas finais.

A menor nota que o candidato II deverá obter na prova final de química para vencer a competição é
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 8 de 10
8. Pergunta
(UNEB BA/2013)
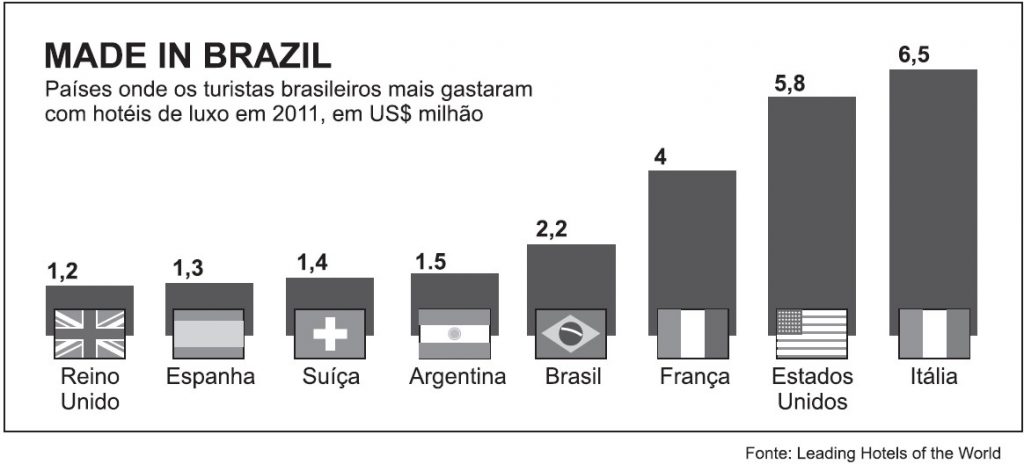
Brasileiros dispostos a pagar diárias que podem chegar a 11 mil (R$ 30,69 mil) por uma suíte são a bola da vez no mercado mundial de hotelaria de luxo.
Disputada pelos mais requintados hotéis, a clientela do Brasil ocupa a terceira posição do ranking de reservas do The Leading Hotels of the World (LHW). O selo reúne alguns dos mais sofisticados estabelecimentos do mundo.
De 2010 para 2011, o faturamento local do LHW cresceu 16,26%.
No ano passado, o escritório brasileiro bateu o recorde de US$ 31 milhões (R$ 66,96 milhões) em reservas. (TURISTA…, 2012, p. B 3).
TURISTA BRASILEIRO ‘AAA’ é 3º do mundo. Folha de S.Paulo.
São Paulo 1 jan. 2012. MERCADO. Adaptado.
(Cotações do câmbio turismo do dia 1 nov. 2012) A mediana dos gastos, em milhões de reais, dos turistas brasileiros com hotéis de luxo, em 2011, é igual a
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre estatística para acertar na hora da prova!
-
Pergunta 9 de 10
9. Pergunta
(UFPR/2016)
Em um grupo de 6 pessoas, a média das idades é 17 anos, a mediana é 16,5 anos e a moda é 16 anos. Se uma pessoa de 24 anos se juntar ao grupo, a média e a mediana das idades do grupo passarão a ser, respectivamente:
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!
-
Pergunta 10 de 10
10. Pergunta
(Fac. Israelita de C. da Saúde Albert Einstein SP/2017)
Dois estatísticos estão em uma sala e a média de suas idades é 37 anos. Um terceiro estatístico entra na sala e a média das idades dessas três pessoas passa a ser 39 anos. Um quarto estatístico entra na sala e a média passa a ser 41 anos. Esse processo continua e a cada estatístico que entra na sala, a média das idades de todos eles aumenta em 2 anos. O número de estatísticos que agora estão na sala, sabendo que o último a entrar tem 83 anos, é
Correto
Parabéns! Siga para a próxima questão.
Incorreto
Resposta incorreta. Revise o conteúdo nesta aula sobre média aritmética para acertar na hora da prova!