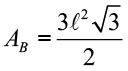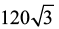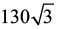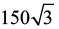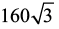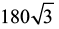Veja uma aula completa para você dominar a classificação, as nomenclaturas e os cálculos de volume e de área dos Prismas. O tema cai direto nas provas do Enem, do Encceja e dos vestibulares. É básico, e dá sim para você aprender e mandar bem. Confira:
Você lembra tudo sobre o Estudo dos Prismas e o cálculos matemáticos envolvidos? A hora de revisar é agora. Todo ano caem questões de cálculo de Área, de Volume, e dos diversos Ângulos também. Veja!
Vamos começar pelo começo. O que e um Prisma? Lembrou da imagem que lhe vem à cabeça? Então, um Prisma é um sólido geométrico delimitado por faces planas, no qual as bases se situam em planos paralelos.
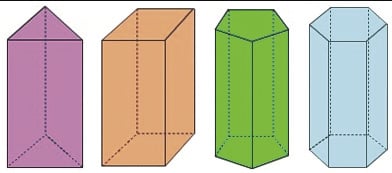
Quanto à inclinação das arestas laterais, os prismas podem ser retos ou oblíquos. Fácil, fácil, não é? Veja nas imagens como fica mais tranquilo de lembrar: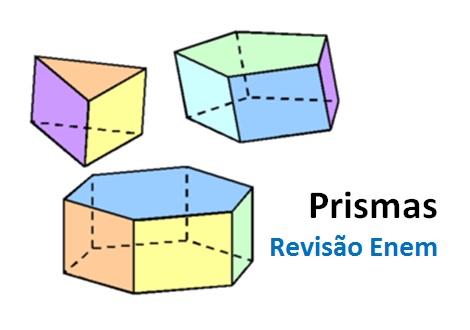
- Características dos Primas:
- Bases: regiões poligonais congruentes
- Altura: distância entre as bases
- Arestas laterais paralelas: mesmas medidas
- Faces laterais: paralelogramos
Aula Gratuita: A Classificação dos Prismas
Confira um resumo simples e rápido com o professor Sérgio Sarkis para você dominar os tipos de Primas que caem no Enem, no Encceja ou nos vestibulares.
Show o resumo do professor Sarkis. Agora, vamos em frente aqui:
Prisma reto
- As arestas laterais têm o mesmo comprimento.
- As arestas laterais são perpendiculares ao plano da base.
- As faces laterais são retangulares.
Prisma oblíquo

- As arestas laterais têm o mesmo comprimento.
- As arestas laterais são oblíquas ao plano da base.
- As faces laterais não são retangulares.
Elementos principais
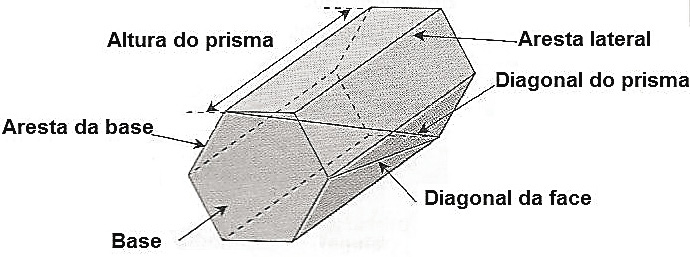
- Aresta da base ( ℓ )
- Aresta lateral ( aℓ )
- Altura do prisma ( H )
Nomenclatura dos Prismas
Os prismas recebem nomes de acordo com a figura poligonal de sua base.
Exemplo
- Prisma triangular : a base é um triângulo.
- Prisma quadrangular: a base é um quadrilátero
- Prisma pentagonal: a base é um pentágono.
Prismas Regulares
São prismas que apresentam polígonos regulares em sua base.
Exemplo:
- Prisma Triangular Regular: a base é um triângulo equilátero.
- Prisma Quadrangular Regular: a base é um quadrado.
- Prisma Hexagonal Regular: a base é um hexágono regular.
Aula Gratuita de Geometria Espacial
Veja como fazer o cálculo de volume e de área nos poliedros com o professor Sérgio Sarkis
Agora, veja as fórmulas mais utilizadas no cálculo de áreas e volumes nos Prismas:
Cálculo de Áreas e Volume nos Prismas (Prisma reto regular)
Área da base (AB)
Calculada de acordo com o nome do prisma. Considere ℓ como a aresta da base.
- Prisma Triangular regular:
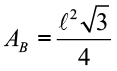
- Prisma Quadrangular Regular:
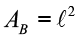
- Prisma Hexagonal Regular:

Área lateral (AL)
As faces são retangulares assim basta calcular a área de uma face e multiplicar o valor pelo número de faces (sempre igual ao número de lados da base).
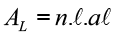
Área total
Corresponde a soma da área lateral com as duas bases do prisma
AT = AL + 2.AB
Volume (V)
É o resultado da multiplicação da área da base pela altura do prisma. Observe que nos prismas retos a altura é igual à aresta lateral do prisma, ou seja,
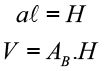
Dicas do Blog do Enem – Matemática:
Dica 1 – Você sabe tudo sobre os Polígonos Regulares? Revise aqui as definições e classificações de Polígonos Regulares em mais uma aula de Matemática Enem
Dica 2 – Relembre aqui sobre Ângulos na Circunferência em mais esta aula preparatória para a prova de Matemática Enem. Estude com a gente, o Enem está chegando!
Desafios para você responder e compartilhar as soluções nas redes sociais
Questão 01
Deseja-se construir um prédio para armazenamento de grãos em forma de um prisma regular de base triangular, cuja aresta da base meça 8 m e altura do prisma tenha 10 m. O volume
interno desse armazém em m³ será:
|
a) |
|
|
b) |
|
|
c) |
|
|
d) |
|
|
e) |
|
Dica 3 – Você sabe a diferença entre um círculo e uma circunferência? Nesta aula de Matemática Enem você pode revisar tudo sobre essas duas formas geométricas – https://blogdoenem.com.br/circulo-e-circunferencia-matematica-enem/
Questão 02
Em uma usina de compostagem, após a triagem, o material é colocado em canteiros, aproximadamente com a forma de um prisma triangular reto, e revolvido periodicamente, até se obter a cura do composto.
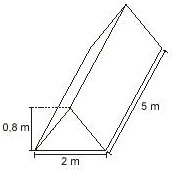
Se num determinado momento há no pátio 9 desses canteiros, a quantidade de composto existente é, em metros cúbicos, igual a
a) 36
b) 30
c) 28
d) 24
e) 15
Questão 03
Uma fábrica de embalagens, para atender a uma encomenda, deve produzir uma caixa na forma de um prisma retangular reto, com capacidade para 8 litros (lembre-se que 1litro = 1dm3). Nessa encomenda está especificado que as dimensões da caixa, em decímetros, devem ser x, x-1 e 2x. Então, o número de possíveis valores distintos para x é:
a) zero.
b) um.
c) dois.
d) três.
e) quatro.
Questão 04
De uma viga de madeira de seção quadrada de lado 10cm, extrai-se uma cunha de madeira de altura 15cm, conforme a figura:
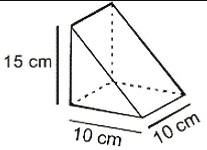
O volume da cunha é:
a) 250cm3
b) 500cm3
c) 750cm3
d) 1000cm3
e) 1250cm3
Questão 05
Um recipiente na forma de um prisma reto de base quadrada, cuja área lateral é igual ao sêxtuplo da área da base, contém um determinado medicamento que ocupa 75% de sua capacidade total. Conforme prescrição médica, três doses diárias desse medicamento, com 50 ml cada uma, deverão ser ministradas a um paciente durante seis dias. Nessas condições, é correto afirmar que, para ministrar a quantidade total prescrita, o medicamento contido nesse recipiente será:
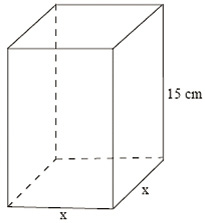
a) insuficiente, faltando, 125 ml
b) insuficiente, faltando, 120 ml
c) suficiente, não restando nada.
d) suficiente, restando 125 ml.
e) suficiente, restando 225 ml.
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!