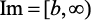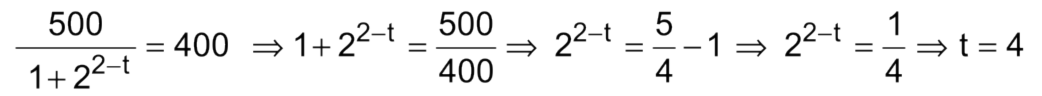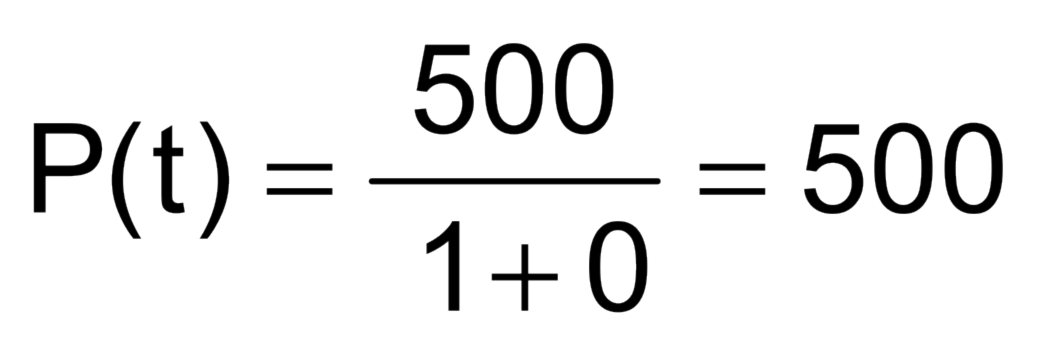Revise sobre as equações exponenciais e tire suas dúvidas em exercícios resolvidos em mais esta aula de Matemática Enem que preparamos para você
Você lembra das aulas e dos conteúdos sobre Equações Exponenciais? – É hora de revisar. Vamos lá! Exponencial é toda equação que pode ser reduzida a forma ax = b, com 0 < a ≠ 1.
- – Complicou? Então, vamos facilitar:
- A base das nossas potências não pode ser qualquer número, ela deve ser necessariamente maior que zero e diferente de 1, de acordo com a definição das funções exponenciais
Vamos seguir com outros olhares sobre a Equação Exponencial…
- Uma equação exponencial pode ser reduzida a forma ax = b, com 0 < a ≠ 1
- Para resolver tais equações é necessário transformar a equação dada em:
- Igualdade de potência de mesma base: af(x)= ag(x) → f(x) = g(x); e, ainda,
- Com Potências de expoentes iguais: af(x) = bf(x) → a = b, sendo a e b ≠ 1 e a e b ∈ R*+

Mas, dominar a definição não adianta. O que vale ponto , mesmo, é resolver as questões do Enem, do Encceja e dos Vestibulares.
- Para resolver tais equações, é necessário consolidar o aprendizado inicial. Veja agora de outra forma: É preciso transformar a equação dada em:
- Igualdade de potência de mesma base.
- af(x) = ag(x) f(x) =g(x)
- Potências de expoentes iguais. af(x) = bf(x) a = b sendo a e b ≠1 e a e b
 R*+.
R*+.
Estude com nossa videoaula e prepare-se para o Enem
A Função Exponencial
Chama-se função exponencial toda função que pode ser reduzida a forma f(x)= ax + b, a >0 e b ≠ 1.
Veja agora como fica nos gráficos:
Para a > 1, a função é Crescente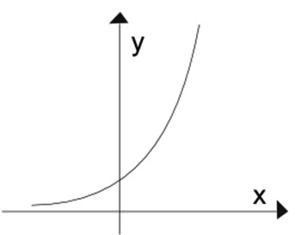
Para 0 < a < 1, a função é Decrescente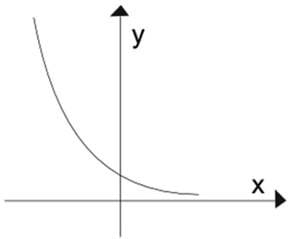
A Imagem da função
- Seja a função f(x)= ax + b
- Temos que sua imagem será

Exercício resolvido sobre função exponencial:
(UFPR, 2012) – Um grupo de cientistas decidiu utilizar o seguinte modelo logístico, bastante conhecido por matemáticos e biólogos, para estimar o número de pássaros, P(t), de determinada espécie numa área de proteção ambiental. Sendo t o tempo em anos e t = 0 o momento em que o estudo foi iniciado.
- a) Em quanto tempo a população chegará a 400 indivíduos?
- Resolução:

- b) À medida que o tempo t aumenta, o número de pássaros dessa espécie se aproxima de qual valor? Justifique sua resposta.
- Resolução: Para t muito grande, o valor 22-t tende a ser 0; logo, P(t) será dado por

- Portanto, o número de pássaros dessa espécie se aproxima a 500.
Veja outro exercício resolvido – (Ufpr 2012) Um grupo de cientistas decidiu utilizar o seguinte modelo logístico, bastante conhecido por matemáticos e biólogos, para estimar o número de pássaros, P(t), de determinada espécie numa área de proteção ambiental:
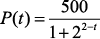 ,
,
sendo t o tempo em anos e t = 0 o momento em que o estudo foi iniciado.
a) Em quanto tempo a população chegará a 400 indivíduos?
Resolução: Para t=? temos P(t)=400
Portanto
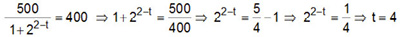
b) À medida que o tempo t aumenta, o número de pássaros dessa espécie se aproxima de qual valor? Justifique sua resposta.
Resolução: Para t muito grande, o valor 22-t tende a ser 0; logo, p(t) será dado por
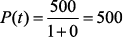
Portanto, o número de pássaros dessa espécie se aproxima a 500.
Desafios para você resolver e compartilhar as respostas
Questão 1
(Espm 2012) A figura abaixo mostra o gráfico da função f(x) = 2x. A área da região sombreada, formada por retângulos, é igual a:
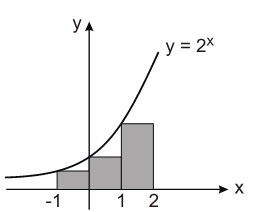
a) 3,0
b) 3,5
c) 4,0
d) 4,5
e) 5,0
Dica 2 – Tire todas as suas dúvidas sobre Funções Polinomiais de 2o grau em mais esta aula de revisão para a prova de Matemática Enem que preparamos para você – https://blogdoenem.com.br/funcao-polinomial-2o-grau-revisao-matematica-enem/
Questão 2
(Uel 2008) Seja a equação exponencial: 9x + 3 = (1/27)x
Assinale a alternativa que contém a solução da equação exponencial dada.
a) x = – 6
b) x = – 6/5
c) x = 5/6
d) x = 5/2
e) x = 6
Dica 3 – O dia das provas está chegando, que tal revisar algumas aulas importantes. Revise tudo sobre Função Polinomial do 1º grau nesta aula de Matemática Enem – https://blogdoenem.com.br/funcao-polinomial-do-1o-grau-matematica-enem/
Questão 3
(G1 – cftmg 2007) Se (x, y) é a solução do sistema
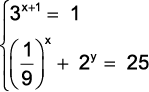
então, a diferença (y – x) é igual a
a) 2
b) 3
c) 4
d) 5
Questão 4
(Ufjf 2006) Dada a equação 23x – 2 . 8x + 1 = 4x – 1, podemos afirmar que sua solução é um número:
a) natural.
b) maior que 1.
c) de módulo maior do que 1.
d) par.
e) de módulo menor do que 1.
Questão 5
(G1 – cftmg 2004) A soma das raízes da equação
4x+ 1 – 9 . 2x + 2 = 0 é
a) -2
b) -1
c) 0
d) 1
Você consegue resolver estes exercícios? Então resolva e coloque um comentário no post, logo abaixo, explicando o seu raciocínio e apontando a alternativa correta para cada questão. Quem compartilha a resolução de um exercício ganha em dobro: ensina e aprende ao mesmo tempo. Ensinar é uma das melhores formas de aprender!
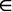 R*+.
R*+.